曲線残差プロットを解釈する方法 (例付き)

残差プロットは、回帰モデルの残差が正規分布しているかどうか、また残差が不均一分散性を示しているかどうかを評価するために使用されます。

理想的には、残差プロット内の点が、明確なパターンがなく、値 0 の周囲にランダムに散在していることが望まれます。

プロット点が曲線パターンを持つ残差プロットが発生した場合は、データに対して指定した回帰モデルが正しくないことを意味している可能性があります。

ほとんどの場合、これは、代わりに二次トレンドに従うデータセットに線形回帰モデルを当てはめようとしたことを意味します。

次の例は、実際に曲線残差プロットを解釈 (および修正) する方法を示しています。

例: 曲線残差プロットの解釈

オフィス内の 11 人の異なる従業員について、週あたりの労働時間数と報告された幸福度 (0 から 100 のスケール) に関する次のデータを収集するとします。

労働時間と幸福度の単純な散布図を作成すると、次のようになります。

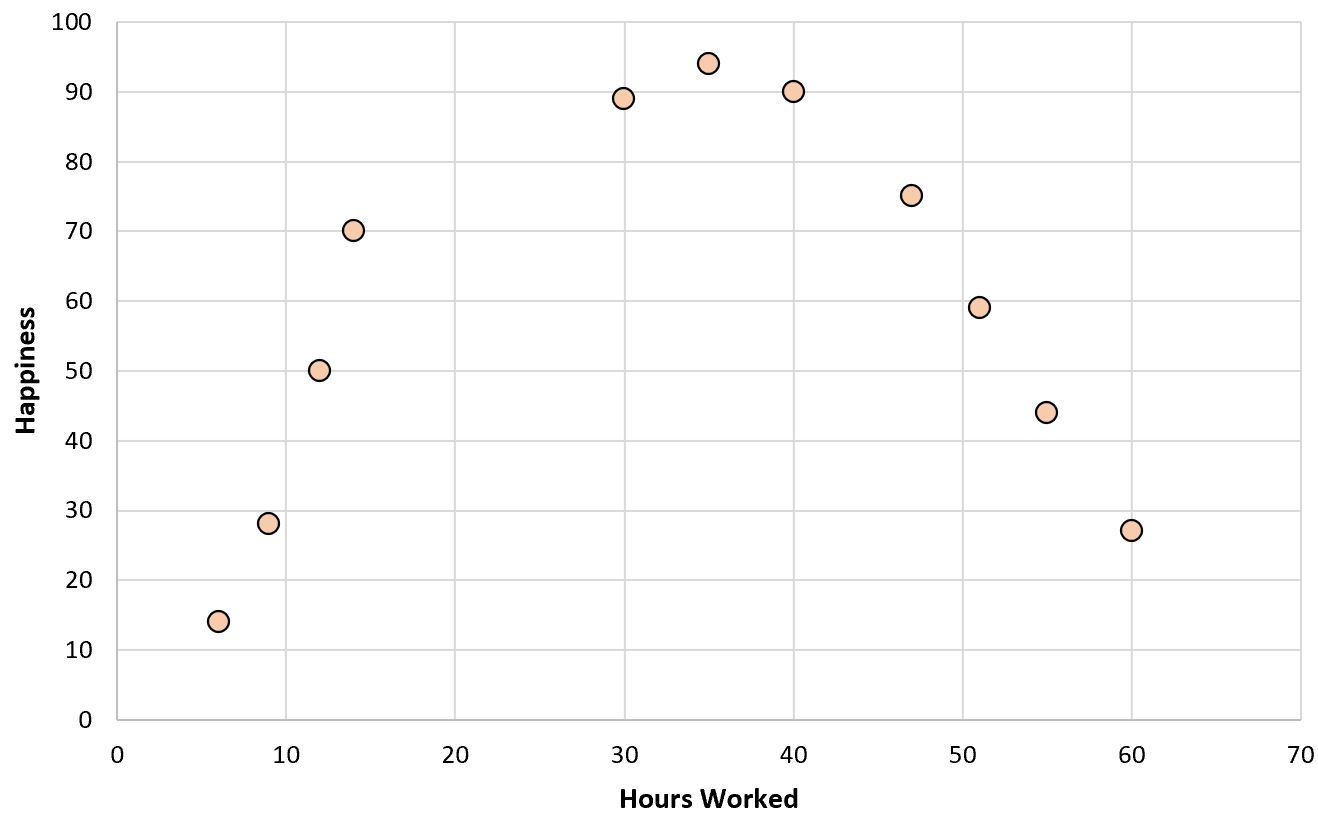
ここで、幸福度を予測するために労働時間を使用して回帰モデルを当てはめたいとします。

次のコードは、単純な線形回帰モデルをこのデータセットに近似し、R で残差プロットを生成する方法を示しています。

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

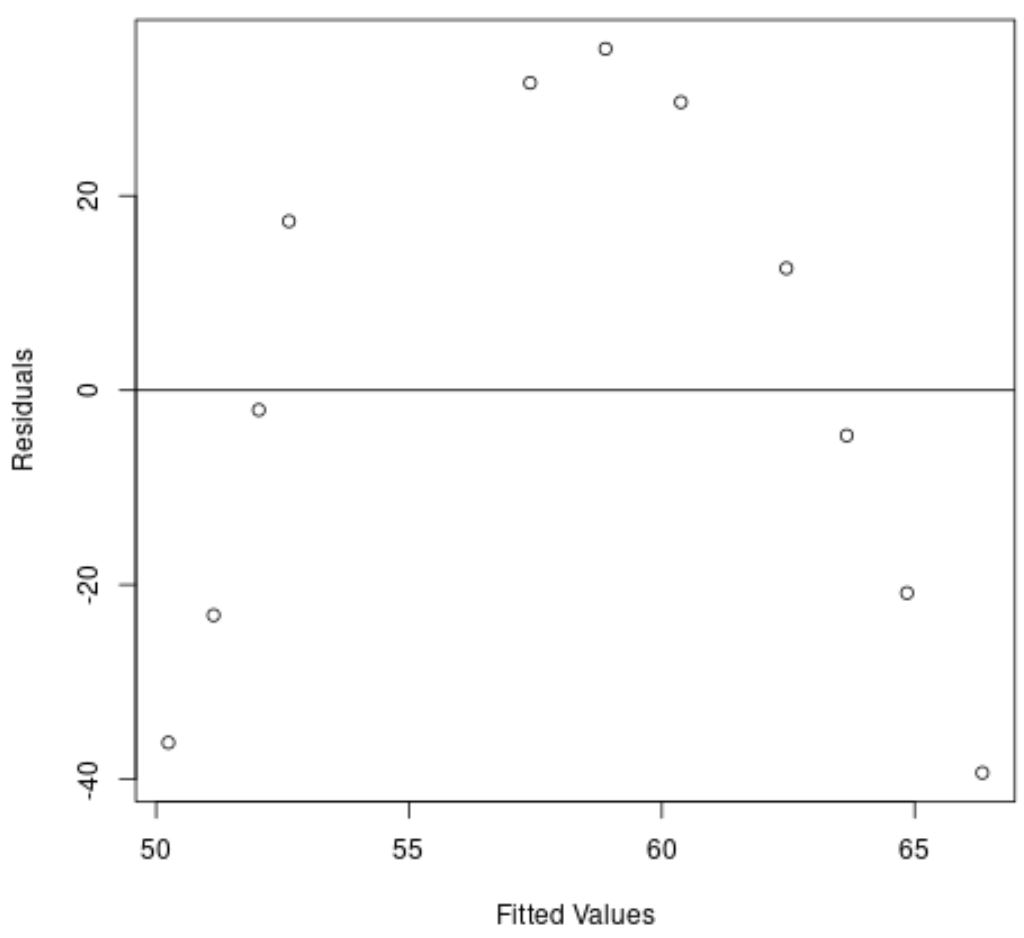
X 軸は近似値を表示し、Y 軸は残差を表示します。

グラフから、残差に曲線のパターンがあることがわかり、線形回帰モデルがこのデータセットに適切に適合しないことを示しています。

次のコードは、二次回帰モデルをこのデータセットに近似し、R で残差プロットを生成する方法を示しています。

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

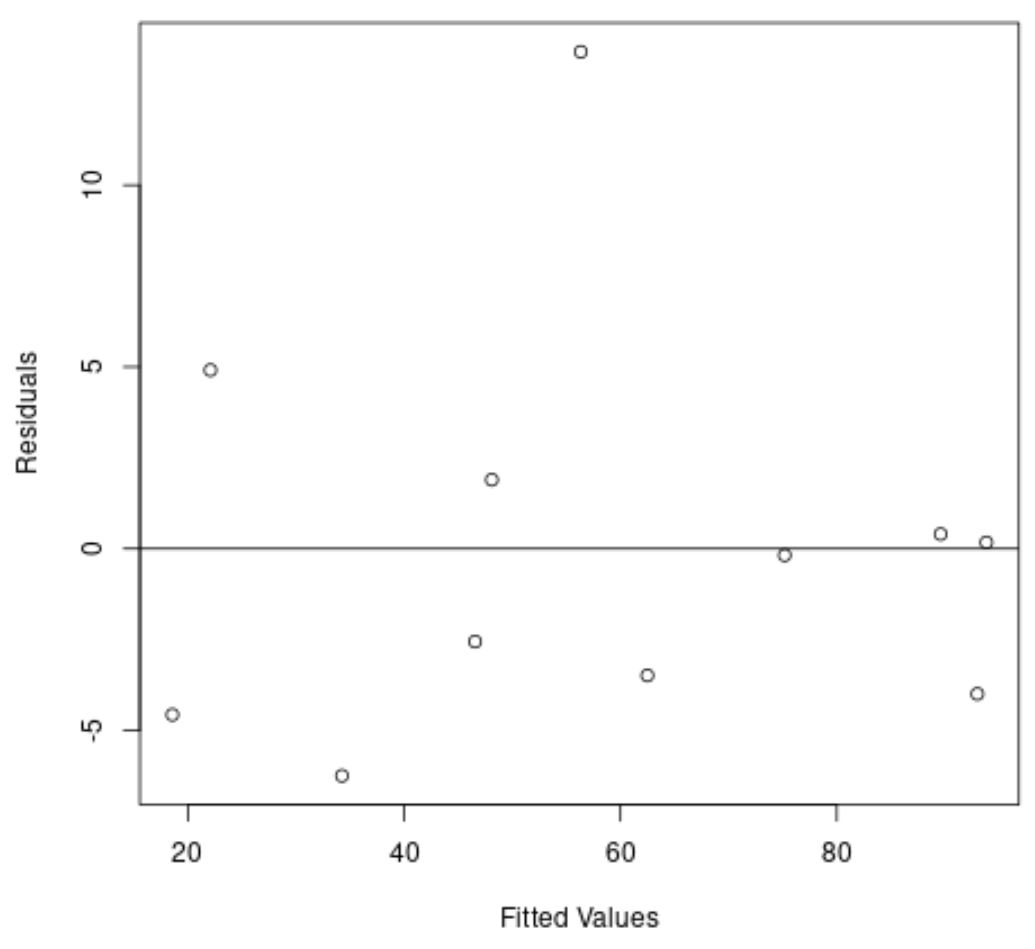
もう一度言いますが、X 軸は近似値を示し、Y 軸は残差を示します。

プロットから、残差がゼロの周りにランダムに分散しており、残差に明確な傾向がないことがわかります。

これは、二次回帰モデルが線形回帰モデルよりもこのデータセットの適合にはるかに優れていることを示しています。

労働時間と幸福度の間の実際の関係が線形ではなく二次関数であるように見えることを考えると、これは当然のことです。

追加リソース

次のチュートリアルでは、さまざまな統計ソフトウェアを使用して残差プロットを作成する方法を説明します。

残りのパスを手動で作成する方法
R で残差プロットを作成する方法
Excel で残差プロットを作成する方法
Python で残差プロットを作成する方法