フィッシャーの最小有意差: 定義 + 例
一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。
ANOVA で使用される仮定は次のとおりです。
H 0 : 平均は各グループで等しい。
H A : 少なくとも 1 つの方法は他の方法とは異なります。
ANOVA のp 値が特定の有意レベル (α = 0.05 など) を下回っている場合、帰無仮説を棄却し、グループ平均の少なくとも 1 つが他の平均とは異なると結論付けることができます。
しかし、どのグループが互いに異なっているかを正確に知るには、事後テストを行う必要があります。
一般的に使用される事後検定は、フィッシャーの最小有意差検定です。
このテストを実行するには、まず次のテスト統計を計算します。
LSD = t 0.025 , DF w * √ MS W (1/n 1 + 1/n 1 )
金:
- t .025 、 DFw : α = .025 および DF wの t 分布テーブルの t 臨界値は、ANOVA テーブルのグループ内の自由度に対応します。
- MS W : ANOVA 表のグループ内の平均二乗。
- n 1 、n 2 :各グループのサンプルサイズ
次に、各グループ間の平均差をこの検定統計量と比較できます。 2 つのグループ間の平均差の絶対値が検定統計量より大きい場合、グループ平均間に統計的に有意な差があると宣言できます。
次の例は、フィッシャーの最小有意差検定を実際に実行する方法を示しています。
例: フィッシャー最小有意差検定
教授が、3 つの異なる学習方法が生徒間でテストの得点に差をもたらすかどうかを知りたいと考えているとします。これをテストするために、彼女は 10 人の生徒をランダムに割り当てて各学習手法を使用させ、試験結果を記録しました。
次の表は、使用した学習手法に基づいた各生徒の試験結果を示しています。

教授は一元配置分散分析を実行し、次の結果を得ました。
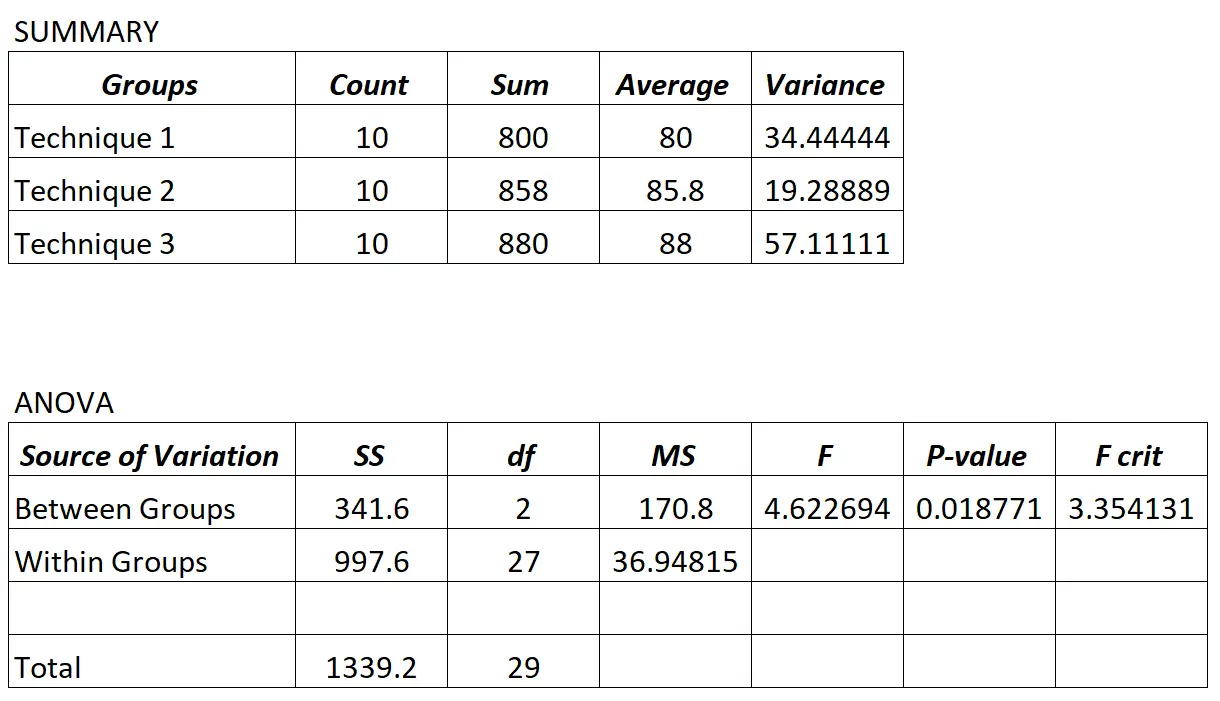
ANOVA 表の p 値 (0.018771) は 0.05 未満であるため、3 つのグループ間の試験の平均点はすべて等しくないと結論付けることができます。
したがって、フィッシャーの最小有意差検定を実行して、どのグループの平均が異なるかを判断できます。
ANOVA 結果の値を使用して、次のようにフィッシャー テスト統計量を計算できます。
- LSD = t 0.025 , DFw * √ MS W (1/n 1 + 1/n 1 )
- LSD = t 0.025 , 27 * √ 36.948*(1/10 + 1/10)
- LSD = 2.052 * √ 7.3896
- LSD = 5.578
次に、各グループ間の絶対平均差を計算できます。
- テクニック 1 とテクニック 2: |80 – 85.8| = 5.8
- テクニック 1 とテクニック 3: |80 – 88| = 8
- テクニック 2 とテクニック 3: |85.8 – 88| = 2.2
テクニック 1 とテクニック 2 の間、およびテクニック 1 とテクニック 3 の間の絶対平均差は、フィッシャー テスト統計よりも大きくなります。したがって、これらのテクニックは統計的に有意に異なる試験平均点につながると結論付けることができます。
また、テクニック 2 とテクニック 3 の間で試験の平均点に大きな差はないと結論付けることもできます。