フィッシャーの正確検定: 定義、公式、および例
フィッシャーの直接確率検定は、 2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。これは通常、2 × 2 テーブル内の 1 つ以上のセル数が 5 未満である場合に、独立性のカイ二乗検定の代替として使用されます。
フィッシャーの正確検定では、次の帰無仮説と対立仮説が使用されます。
- H 0 : (帰無仮説) 2 つの変数は独立しています。
- H 1 : (対立仮説) 2 つの変数は独立していません。
次の 2×2 テーブルがあるとします。
| グループ1 | グループ2 | 行合計 | |
| カテゴリー1 | もっている | b | a+b |
| カテゴリー2 | 対 | d | c+d |
| 合計欄 | a+c | b+d | a+b+c+d = n |
フィッシャーの直接確率検定の片側 p 値は次のように計算されます。
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
これにより、次のパラメーターを使用して超幾何分布の CDF と同じ p 値が生成されます。
- 集団サイズ = n
- 人口の「成功」 = a+b
- サンプルサイズ = a + c
- 「成功」の例 = 1
フィッシャーの正確検定の両側 p 値は計算がそれほど簡単ではなく、片側 p 値を単に 2 で乗算するだけでは求めることができません。両側 p 値を見つけるには、 フィッシャーの正確検定計算機を使用することをお勧めします。
フィッシャーの正確検定: 例
性別が政党の好みと関連しているかどうかを知りたいとします。 25 人の有権者から単純に無作為にサンプルを抽出し、政党の好みについて尋ねます。次の表は、調査の結果を示しています。
| 民主党 | 共和党 | 合計 | |
| 男 | 4 | 9 | 13 |
| 女性 | 8 | 4 | 12 |
| 合計 | 12 | 13 | 25 |
ステップ 1: 前提条件を定義します。
次の仮定を使用してフィッシャーの正確確率検定を実行します。
- H 0 :性別と政党の好みは独立しています。
- H 1 :性別と政党の好みは独立していません。
ステップ 2: 両側 p 値の計算。
次の入力を使用してフィッシャーの正確検定計算機を使用できます。
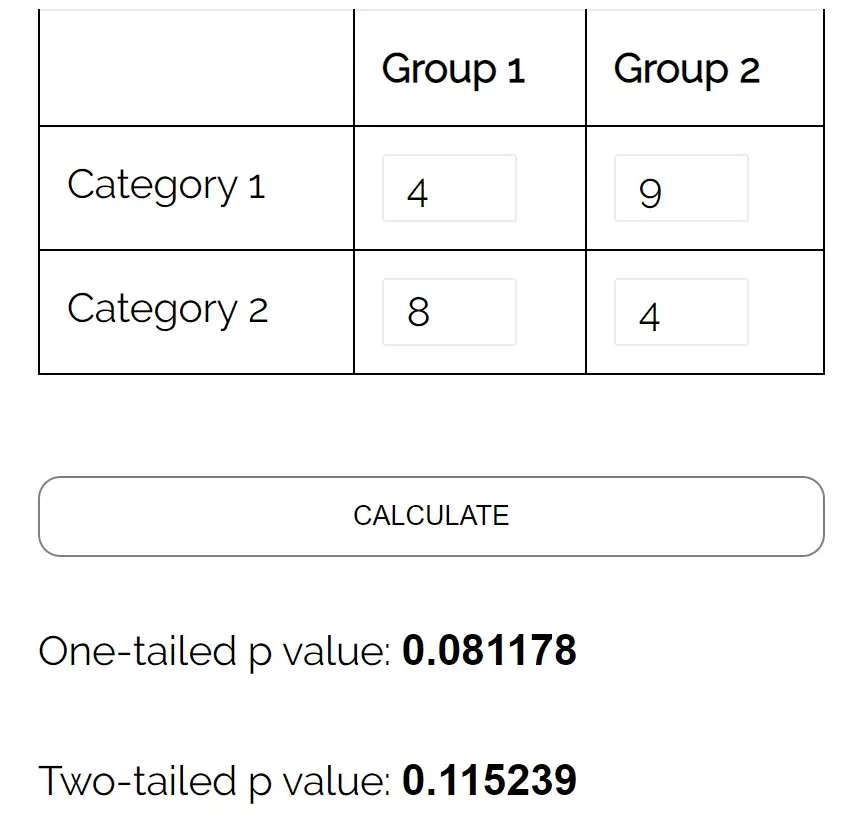
両側 p 値は0.115239です。この値が 0.05 未満であるため、帰無仮説を棄却できません。性別と政党の好みとの間に統計的に有意な関連があると言える十分な証拠はありません。
追加リソース
次のチュートリアルでは、さまざまな統計プログラムを使用してフィッシャーの正確確率検定を実行する方法を説明します。
R でフィッシャーの正確検定を実行する方法
Excel でフィッシャーの正確確率検定を実行する方法
Stata でフィッシャーの正確確率検定を実行する方法
SPSS でフィッシャーの正確確率検定を実行する方法
Python でフィッシャーの正確テストを実行する方法
フィッシャーの正確検定計算機