Excel でオッズ比と相対リスクを計算する方法

次の形式の 2 × 2 テーブルで分析を実行する場合、オッズ比と相対リスクをよく使用します。

オッズ比は、治療グループで発生する事象の確率と対照グループで発生する事象の確率の比率を示します。次のように計算されます。

オッズ比= (A*D) / (B*C)

相対リスクは、治療グループでイベントが発生する確率と対照グループでイベントが発生する確率の比率を示します。次のように計算されます。

相対リスク= [A/(A+B)] / [C/(C+D)]

このチュートリアルでは、Excel でオッズ比と相対リスクを計算する方法を説明します。

オッズ比と相対リスクの計算方法

50 人のバスケットボール選手が新しいトレーニング プログラムを使用し、50 人の選手が古いトレーニング プログラムを使用しているとします。プログラムの最後に、各プレーヤーが特定のスキル テストに合格するかどうかをテストします。

次の表は、使用したプログラムに基づいて、合格したプレーヤーと不合格になったプレーヤーの数を示しています。

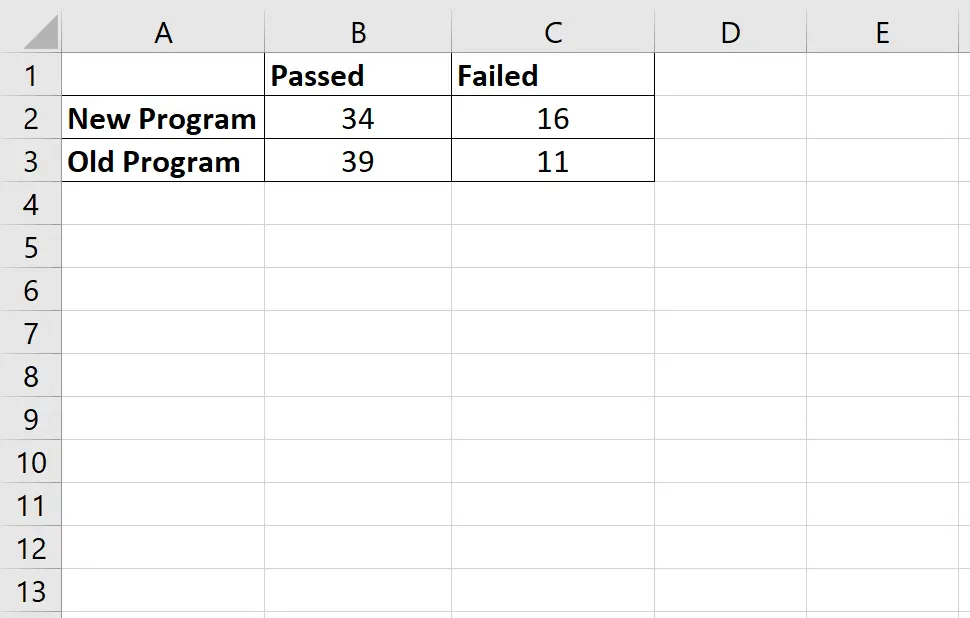
オッズ比は次のように計算されます: (34*11) / (16*39) = 0.599

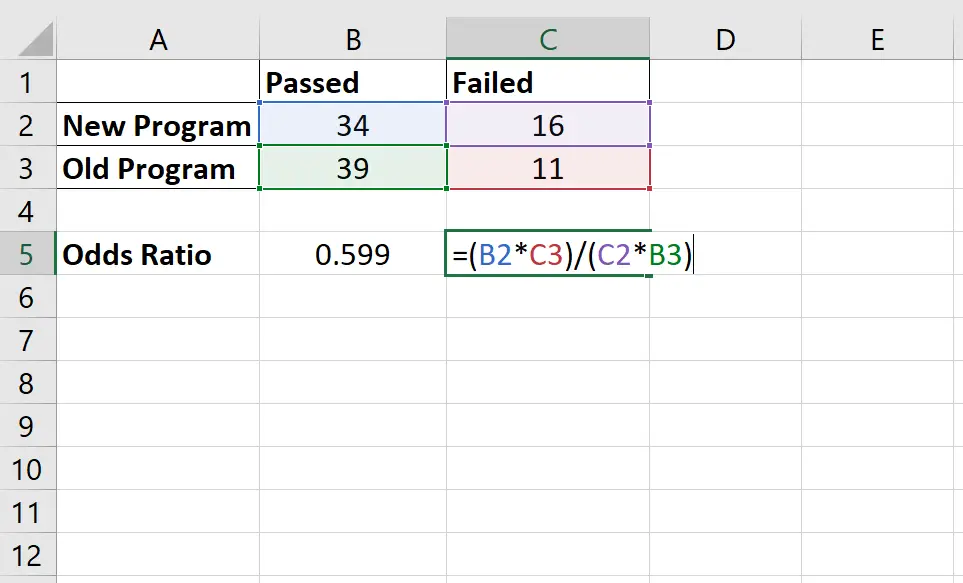
これは、プレーヤーが新しいプログラムを使用してテストに合格する確率は、プレーヤーが古いプログラムを使用してテストに合格する確率の 0.599 倍しかないことを意味すると解釈します。

言い換えれば、新しいプログラムのおかげで、プレーヤーがテストに合格する可能性は実際には 40.1% 減少します。

相対リスクは次のように計算されます: [34/(34+16)] / [39/(39+11)] = 0.872

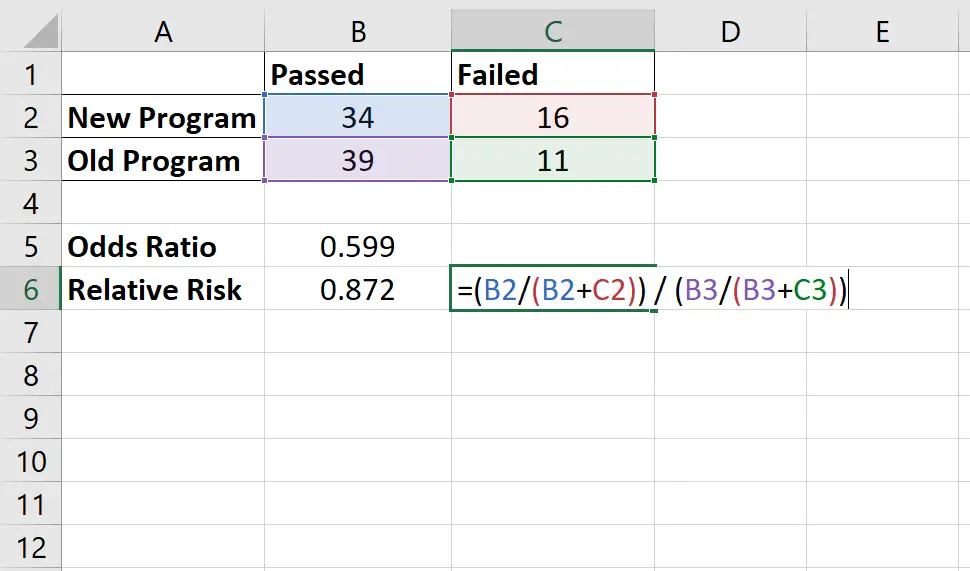
これは、新しいプログラムと古いプログラムを使用してプレーヤーがテストに合格する確率の比率が0.872であることを意味すると解釈します。

この値は 1 未満であるため、実際には、新しいプログラムの方が古いプログラムよりも成功の確率が低いことを示します。

これは、プレーヤーが各プログラムでパスする確率を直接計算することによっても確認できます。

新しいプログラムでの成功確率 = 34/50 = 68%

古いプログラムでの成功確率 = 39/50 = 78%

信頼区間の計算方法

オッズ比と相対リスクを計算したら、これら 2 つの尺度の信頼区間を計算することもできます。

オッズ比の 95% 信頼区間は、次の式を使用して計算できます。

オッズ比の 95% CI = [ e^(ln(OR) – 1.96*SE(ln(OR))), e^(ln(OR) – 1.96*SE(ln(OR) )) ]

ここで、SE(ln(OR)) =√ 1/A + 1/B + 1/C + 1/D

オッズ比の 95% CI は(0.245, 1.467)であることがわかりました。以下の画像は、この信頼区間の計算に使用した式を示しています。

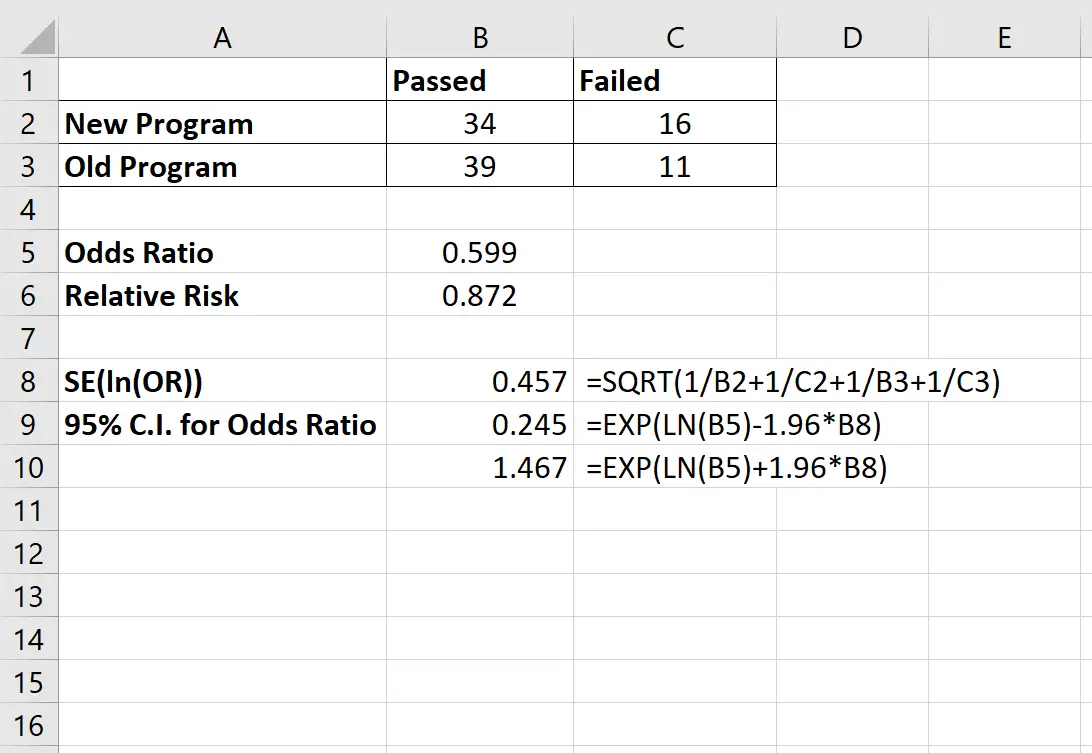
相対リスクの 95% 信頼区間は、次の式を使用して計算できます。

相対リスクの 95% CI = exp(ln(RR) – 1.96*SE(ln(RR))) から exp(ln(RR) – 1.96*SE(ln(RR)))

ここで、SE(ln(RR)) =√ 1/A + 1/C – 1/(A+B) – 1/(C+D)

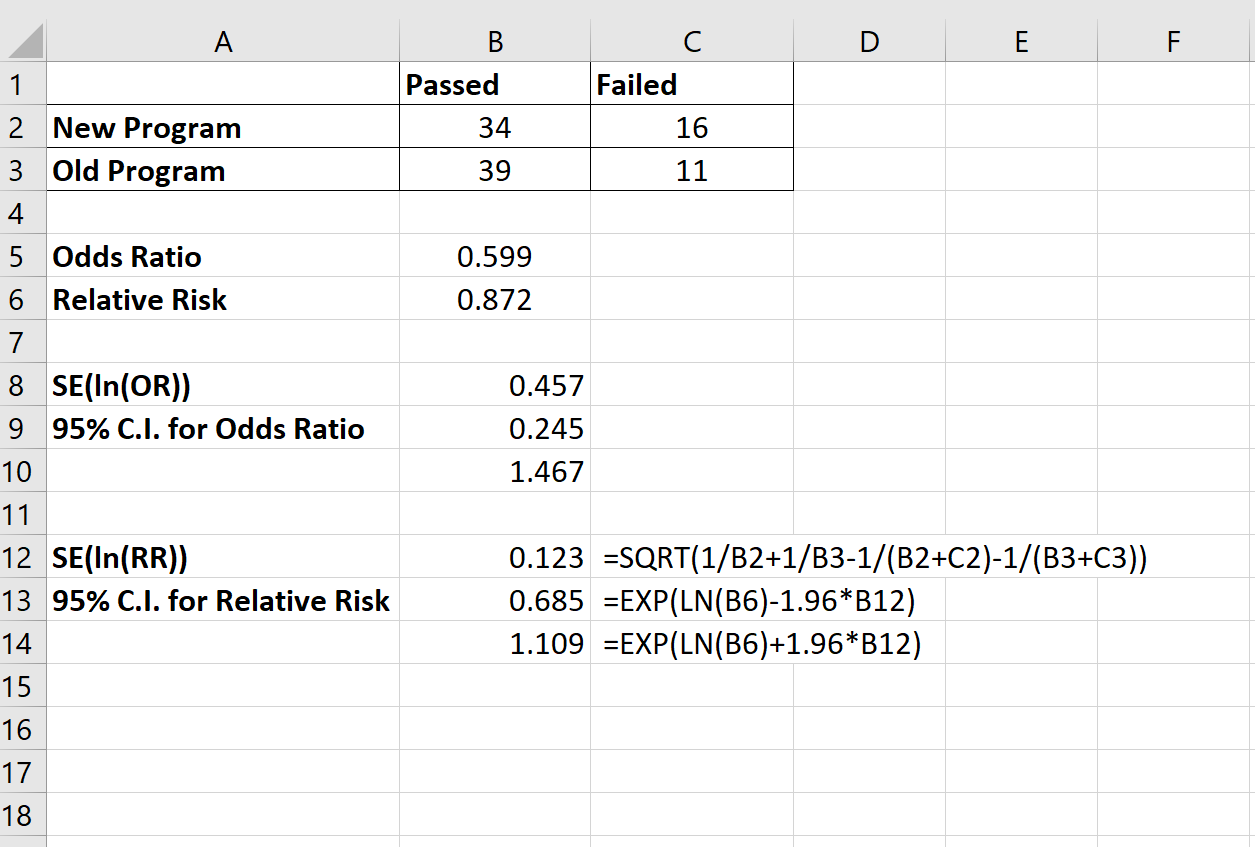
相対リスクの 95% CI は(0.685, 1.109)であることがわかりました。以下の画像は、この信頼区間の計算に使用した式を示しています。

追加リソース

次のチュートリアルでは、オッズ比と相対リスクを解釈する方法に関する追加情報を提供します。

オッズ比の解釈方法
相対リスクをどう解釈するか