相関関係 vs.協会:違いは何ですか?
相関と関連という2 つの用語が同じ意味で使用されることもあります。ただし、統計の分野では、これら 2 つの用語の意味は若干異なります。
特に、 「相関」という言葉を使用する場合、通常は ピアソン相関係数について話します。これは、2 つの確率変数XとYの間の線形関連性の尺度です。値は -1 から 1 までです。ここで、次のとおりです。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
逆に、統計学者が「関連性」という言葉を使用する場合、線形か非線形かにかかわらず、2 つの変数間のあらゆる関係について話している可能性があります。
この考え方を説明するために、次の例を考えてみましょう。
点群との相関と関連性の視覚化
2 つの確率変数間の相関関係を説明するために、次の 2 つの単語を使用します。
1方向
- 正: Xが増加するにつれてY が増加する傾向がある場合、2 つの確率変数は正の相関関係を持ちます。
- 負: Xが増加するにつれてY が減少する傾向がある場合、2 つの確率変数には負の相関があります。
2. 強さ
- 低:散布図内の点がまばらに分散している場合、2 つの確率変数の相関は低くなります。
- 強い:散布図内の点が密接にグループ化されている場合、2 つの確率変数には強い相関関係があります。
次の散布図は、各タイプの相関関係の例を示しています。
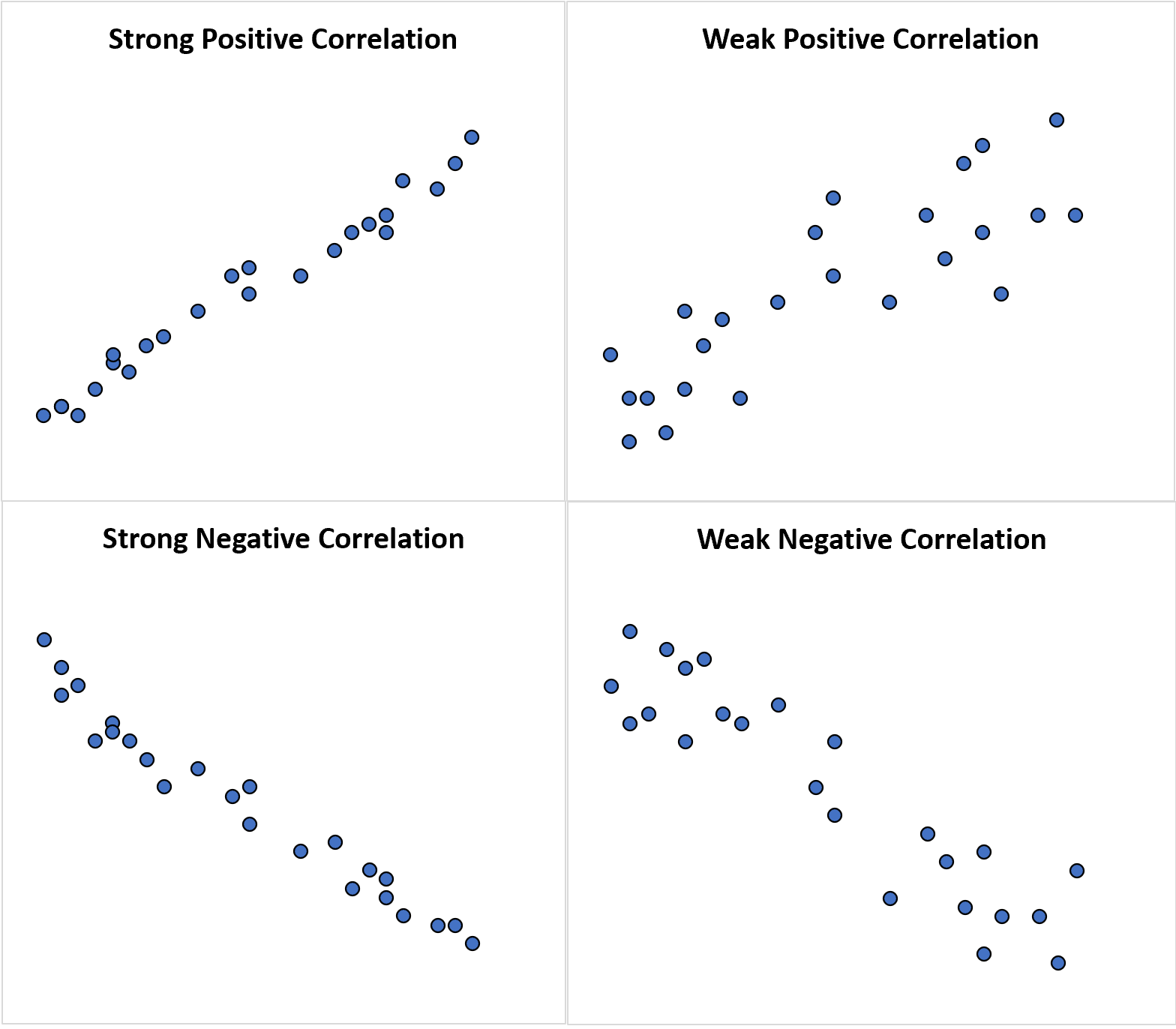
相関関係と比較すると、関連性という言葉は、2 つの確率変数の間に線形か非線形かの関係があるかどうかを示します。
次の散布図はいくつかの例を示しています。
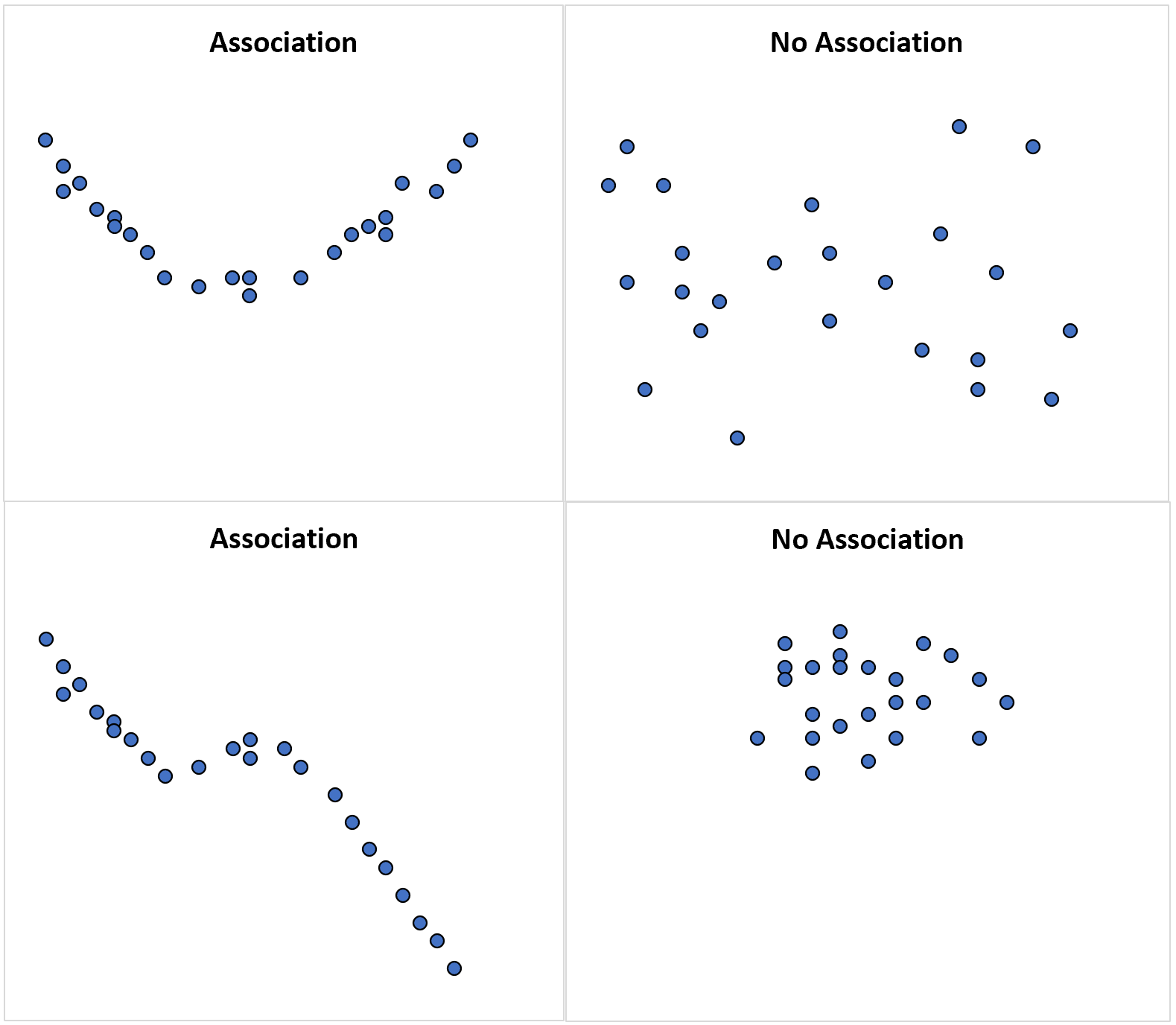
左上隅の散布図は、2 つの確率変数間の二次関係を示しています。これは、2 つの変数間に関連性はあるものの、線形ではないことを意味します。
2 つの変数間の相関関係を計算すると、それらの間に線形関係がないため、相関関係はおそらくゼロに近くなります。
ただし、2 つの変数間の相関関係がゼロであることを単に知っているだけでは、非線形関係が存在するという事実が隠蔽されるため、誤解を招く可能性があります。
相関関係 vs.関連付け: 概要
相関と関連という用語には、次のような類似点と相違点があります。
類似点:
- どちらの用語も、2 つの確率変数間に関係があるかどうかを説明するために使用されます。
- どちらの項も散布図を使用して 2 つの確率変数間の関係を分析できます。
違い:
- 相関関係は 2 つの確率変数が線形関係にあるかどうかのみを示しますが、関連付けは 2 つの確率変数に線形関係があるか非線形関係があるかを示します。
- 相関は、-1 から 1 までの数値を使用して 2 つの確率変数間の関係を定量化しますが、関連は関係を定量化するために特定の数値を使用しません。