省略された変数バイアス: 定義と例
省略された変数のバイアスは、関連する説明変数が回帰モデルに含まれていない場合に発生し、モデル内の 1 つ以上の説明変数の係数にバイアスが生じる可能性があります。
省略された変数は、多くの場合、次の 2 つの理由のいずれかにより回帰モデルから除外されます。
1.変数のデータが単に利用できない。
2. 応答変数に対する説明変数の影響は不明です。
省略された変数が実際にモデル係数を歪めるには、次の 2 つの条件が満たされる必要があります。
1.省略された変数は、モデル内の 1 つ以上の説明変数と関連付けられている必要があります。
2.省略された変数は、モデル内の応答変数と関連付けられている必要があります。
省略された変数バイアスの影響
2 つの説明変数 A と B、および応答変数 Y があるとします。A を唯一の説明変数として単純な線形回帰モデルを当てはめ、B をモデルから除外するとします。
B が A と相関し、 Y と相関している場合、A の係数の推定値に偏りが生じます。次の図は、B との関係の性質に応じて、A の係数の推定値がどのように偏るかを示しています。 B:
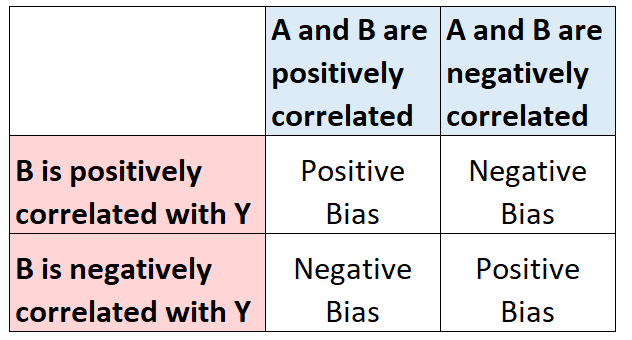
例: 省略された変数バイアス
不動産価格に対する平方フィートの影響を調査したいため、次の単純な線形回帰モデルを適用するとします。
住宅価格 = B 0 + B 1 (平方面積)
推定モデルが次のようになったとします。
住宅価格 = 40,203.91 + 118.31 (平方面積)
平方フィートの係数を解釈する方法は、平方フィートが 1 単位増加するたびに、住宅価格が平均 118.31 ドル上昇することになります。
ただし、面積と強い負の相関があり、不動産価格と強い負の相関があることが判明した説明変数の年齢を省略するとします。この変数はモデル内に存在する必要がありますが、存在しません。したがって、平方フィートの係数推定値にはバイアスがかかっている可能性があります。
年齢はモデルの説明変数と応答変数の両方と負の相関があるため、平方フィートの係数推定値には正のバイアスがかかると予想されます。
住宅の築年数に関するデータを見つけて、それをモデルに含めるとします。モデルは次のようになります。
住宅価格 = B 0 + B 1 (面積) + B 2 (築年数)
推定モデルが次のようになったとします。
住宅価格 = 123,426.20 + 81.06 (面積) – 1,291.04 (築年数)
平方フィートの係数推定値が大幅に減少していることに注意してください。これは、以前のモデルではプラスのバイアスがかかっていたことを意味します。
このモデルの平方フィート係数を解釈する方法は、築年数が一定であると仮定すると、平方フィートが 1 単位増加するたびに、平均住宅価格が 81.06 ドル上昇することになります。
省略された変数のバイアスをどうするか
残念ながら、現実の世界では省略された変数のバイアスが頻繁に発生します。これは、特定の変数は通常、回帰モデルに含まれる必要がありますが、それらのデータが利用できない、またはそれらの変数と応答変数の間の関係が不明なために含まれていないためです。
可能であれば、説明変数と応答変数の間の真の関係を理解できるように、関連するすべての説明変数を回帰モデルに含めるようにしてください。
前の不動産価格の例で見たように、関連する説明変数をモデルから除外すると、モデルの解釈に大きな影響を与える可能性があります。