確率分布の分散を計算する方法
確率分布は、確率変数が特定の値を取る確率を示します。
たとえば、次の確率分布は、特定のサッカー チームが特定の試合で特定の数のゴールを獲得する確率を示します。

確率分布の分散を求めるには、次の公式を使用できます。
σ 2 = Σ(x i -μ) 2 * P(x i )
金:
- x i : i 番目の値
- μ:分布の平均
- P(x i ): i 番目の値の確率
たとえば、フットボール チームの確率分布を考えてみましょう。

サッカー チームの平均ゴール数は次のように計算されます。
μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45ゴール。
次に、次のように分散を計算できます。
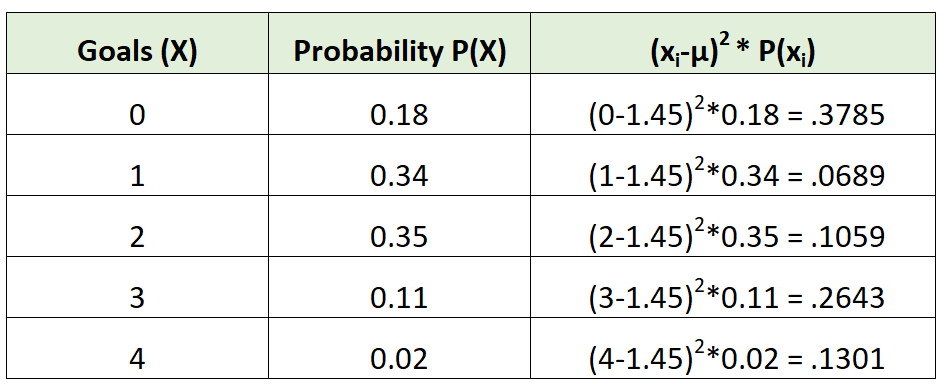
分散は単に 3 列目の値の合計です。したがって、次のように計算します。
σ2 = 0.3785 + 0.0689 + 0.1059 + 0.2643 + 0.1301 = 0.9475
次の例は、他のいくつかのシナリオで確率分布の分散を計算する方法を示しています。
例 1: 車両の故障のばらつき
次の確率分布は、特定の車両が 10 年間に一定回数のバッテリー故障を経験する確率を示しています。
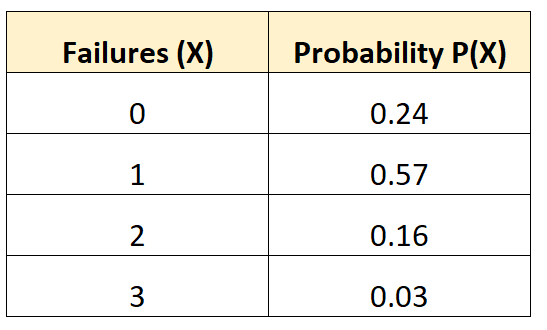
この確率分布の分散を見つけるには、まず予想される失敗の平均数を計算する必要があります。
μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98回の失敗。
次に、次のように分散を計算できます。
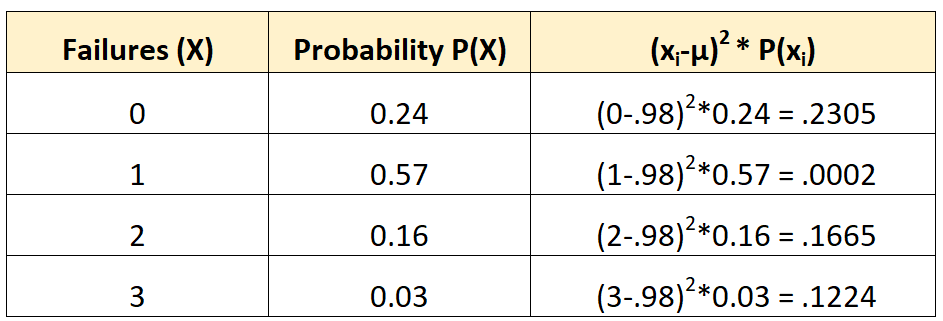
分散は 3 列目の値の合計です。したがって、次のように計算します。
σ2 = 0.2305 + 0.0002 + 0.1665 + 0.1224 = 0.5196
例 2: 売上の変動
次の確率分布は、特定の販売者が来月に特定の数の販売を行う確率を示します。
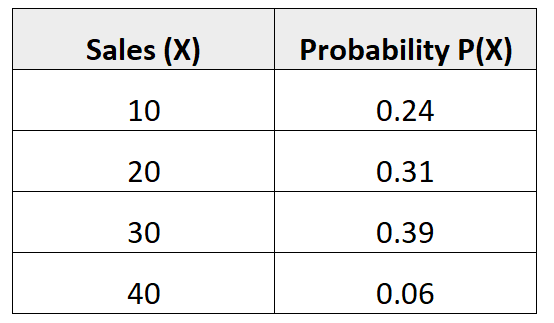
この確率分布の分散を見つけるには、まず予想される販売数の平均を計算する必要があります。
μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7ダーティです。
次に、次のように分散を計算できます。
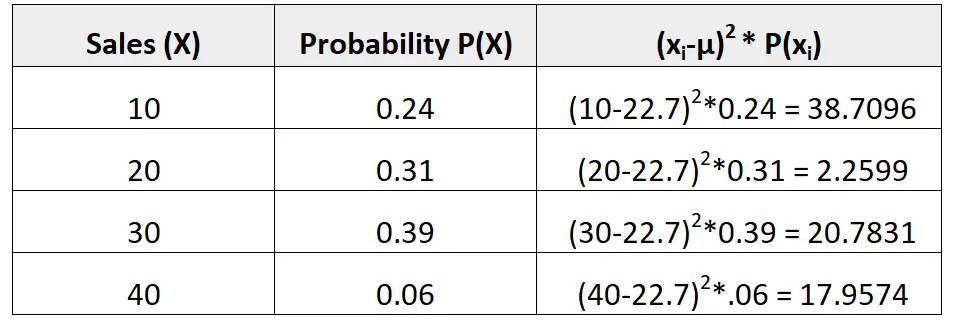
分散は 3 列目の値の合計です。したがって、次のように計算します。
σ2 = 38.7096 + 2.2599 + 20.7831 + 17.9574 = 79.71
確率分布計算ツールを使用して、この分布の分散を自動的に計算することもできることに注意してください。
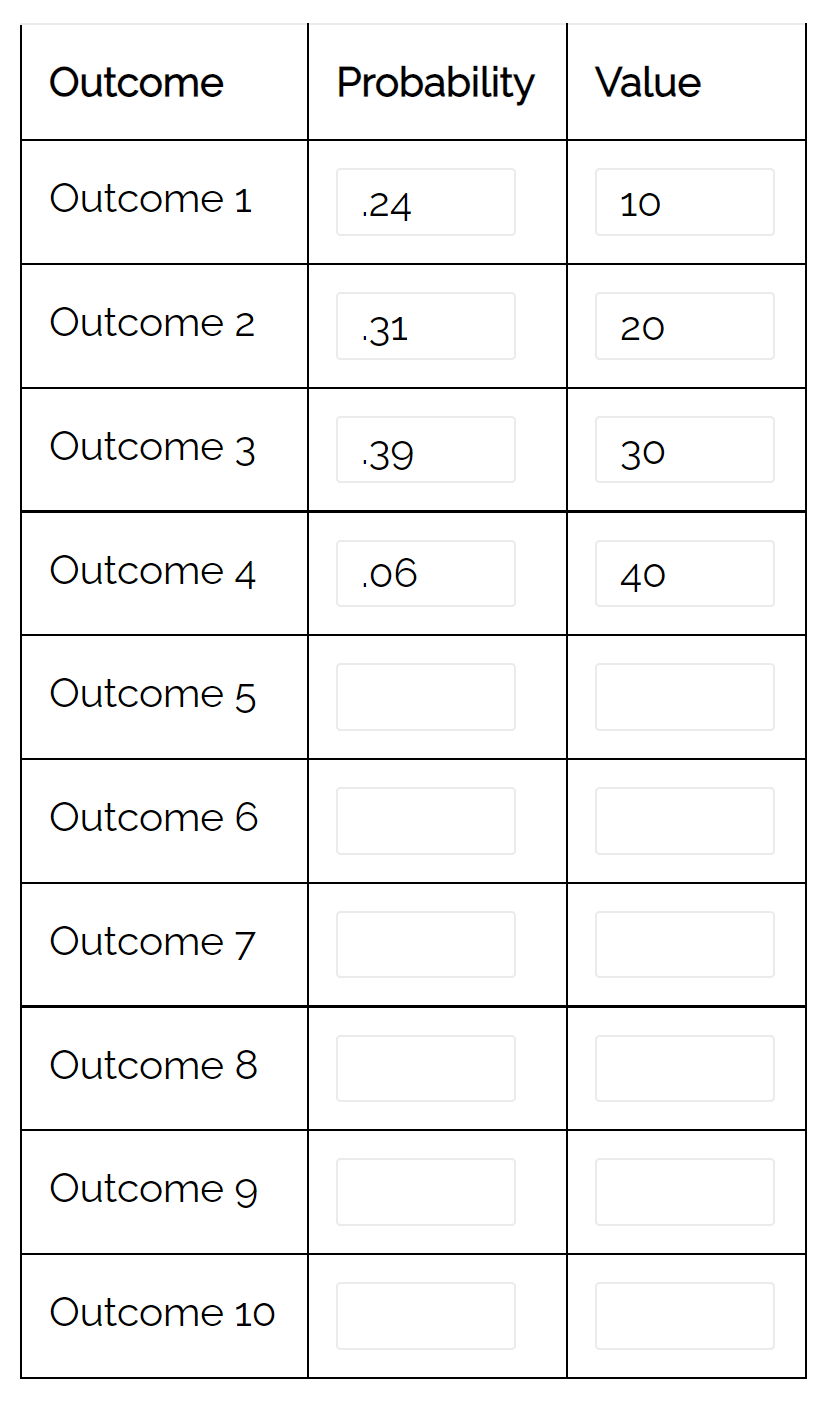

その差は79.71です。これは手動で計算した値に対応します。