確率分布の平均を求める方法: 例付き
確率分布は、確率変数が特定の値を取る確率を示します。
たとえば、次の確率分布は、特定のサッカー チームが特定の試合で特定の数のゴールを獲得する確率を示します。

注:有効な確率分布の確率の合計は常に 1 になります。この確率分布が有効であることを確認できます: 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1。
確率分布の平均(「期待値」と呼ばれることもあります) を求めるには、次の式を使用できます。
Mean (Or "Expected Value") of a Probability Distribution: μ = Σx * P(x) where: •x: Data value •P(x): Probability of value
たとえば、フットボール チームの確率分布を考えてみましょう。

サッカー チームの平均ゴール数は次のように計算されます。
μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45ゴール。
次の例は、他のいくつかのシナリオで確率分布の平均を計算する方法を示しています。
例 1: 車両の平均故障件数
次の確率分布は、特定の車両が 10 年間に一定回数のバッテリー故障を経験する確率を示しています。
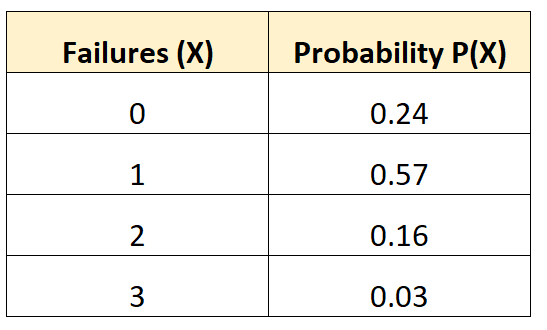
質問:この車両で予想される故障の平均数はどれくらいですか?
解決策:予想される失敗の平均数は次のように計算されます。
μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98回の失敗。
例 2: 平均勝利数
次の確率分布は、特定のバスケットボール チームがトーナメントで特定の試合数に勝つ確率を示します。
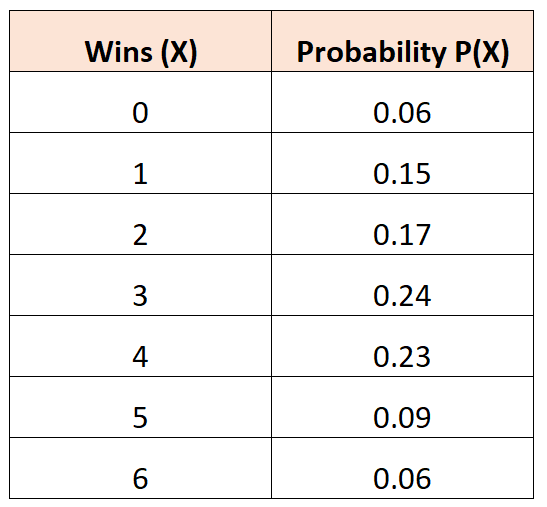
質問:このチームの予想平均勝利数はどれくらいですか?
解決策:予想される勝利の平均数は次のように計算されます。
μ = 0*0.06 + 1*0.15 + 2*0.17 + 3*0.24 + 4*0.23 + 5*0.09 + 6*0.06 = 2.94が勝ちます。
例 3: 平均販売数
次の確率分布は、特定の販売者が来月に特定の数の販売を行う確率を示します。
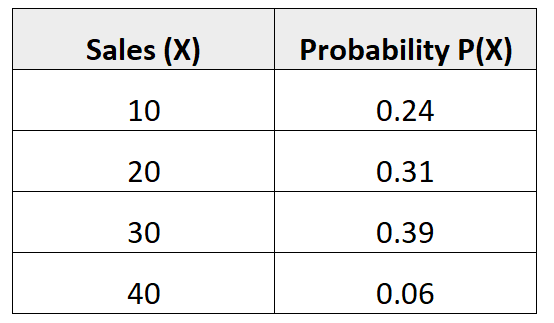
質問:この販売者が来月に予想する平均販売数はどれくらいですか?
解決策:予想販売数の平均は次のように計算されます。
μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7ダーティです。
ボーナス: 確率分布計算機
この計算ツールを使用すると、確率分布の平均を自動的に計算できます。