等分散性

この記事では、統計における等分散性とは何かについて説明します。したがって、等分散性の定義、回帰モデルに等分散性がない原因、およびそれを修正する方法がわかります。

等分散性とは何ですか?

等分散性は、説明変数の誤差が一定の分散を持つ回帰モデルの特性です。つまり、回帰モデルの誤差分散が一定の場合、当該モデルは等分散性を示すため、等分散モデルとなります。

誤差 (または残差) は、実際の値と回帰モデルによって推定された値の差として定義されることに注意してください。

回帰モデルを実行すると、観測ごとに前の式とは異なる値が得られます。したがって、等分散統計モデルは、計算された誤差の分散が観測全体を通じて一定である統計モデルです。

回帰モデルが等分散性を示すことが重要です。実際、これは回帰モデルの以前の仮定の 1 つです。残差が等分散性でない場合は、別の方法でモデルを再実行して等分散性を取得することをお勧めします。そうしないと、回帰係数の推定が誤る可能性が高く、実際には棄却されるべき帰無仮説が受け入れられるため、仮説検定でのエラーも発生します。

等分散性の欠如の原因

モデルに等分散性がない最も一般的な原因は次のとおりです。

• データ範囲が平均と比較して非常に広い場合。同じ統計サンプルに非常に大きな値と非常に小さな値がある場合、得られた回帰モデルは等分散的ではない可能性があります。
• 回帰モデルで変数を省略すると、等分散性が失われます。論理的には、関連する変数がモデルに含まれていない場合、その変動は残差に含まれ、必ずしも固定されるとは限りません。
• 構造が変化すると、モデルのデータセットへの適合が不十分になる可能性があるため、残差の分散は一定ではなくなります。
• 一部の変数の値が他の説明変数よりもはるかに大きい場合、モデルは等分散性を持たない可能性があります。この場合、変数を相対化して問題を解決できます。

ただし、本質的に均一分散性として表現するのが難しいケースもいくつかあります。たとえば、人の収入を食費でモデル化すると、裕福な人は貧しい人よりも食費の変動がはるかに大きくなります。なぜなら、常に安いレストランで食事をする貧しい人とは異なり、金持ちは高いレストランで食事をすることもあれば、安いレストランで食事をすることもあります。したがって、回帰モデルで等分散性を達成することは困難です。

等分散性を達成するためのデータの修正

得られた回帰モデルが等分散性ではない場合、等分散性を達成するために次の修正を試みることができます。

• 独立変数の自然対数を計算します。これは一般に、グラフ内で残差の分散が増加する場合に役立ちます。
• 残差プロットによっては、独立変数の別のタイプの変換の方がより現実的である場合があります。たとえば、グラフが放物線の形状である場合、独立変数の二乗を計算し、その変数をモデルに追加できます。
• 他の変数もモデルに使用できます。変数を削除または追加することにより、残差の分散を変更できます。
• 最小二乗基準を使用する代わりに、加重最小二乗基準を使用できます。

等分散性と不均一分散性

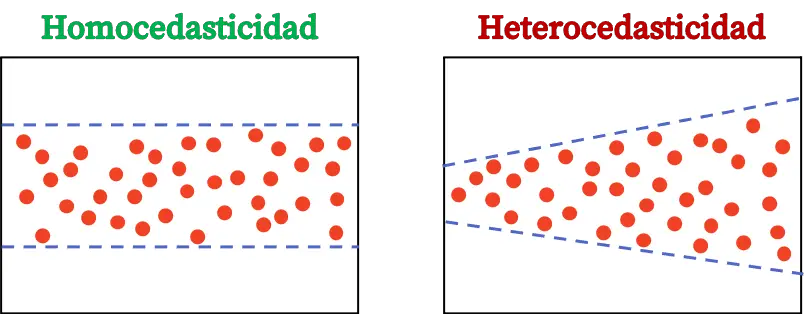
最後に、等分散性と不均一分散性は回帰モデルの 2 つの重要な統計概念であるため、両者の違いは何なのかを見ていきます。

不均一分散性は、回帰モデルの残差が一定の分散をもたないことを意味する統計的特性であり、そのため誤差の変動がプロット全体で同じではありません。

等分散性と不均一分散性の違いは、誤差分散の定常性です。等分散性は誤差の分散が一定であることを意味し、不均一分散性は誤差の分散が一定ではないことを意味します。