箱ひげ図の四分位範囲 (iqr) を見つける方法
箱ひげ図は、データ セットの 5 桁の概要を表示するプロットの一種で、次のものが含まれます。
- 最小値
- 最初の四分位数 (25 パーセンタイル)
- 中央値
- 第 3 四分位数 (75 パーセンタイル)
- 最大値
箱ひげ図を作成するには、第 1 四分位から第 3 四分位までの箱を描きます。次に、中央値に垂直線を引きます。最後に、最小値と最大値までの四分位の「ひげ」を描画します。

四分位範囲(IQR と略されることもよくあります) は、第 3 四分位と第 1 四分位の差です。
- IQR = 第 3 四半期 – 第 1 四半期
これにより、特定のデータセット内の値の中間 50% の分布がわかります。
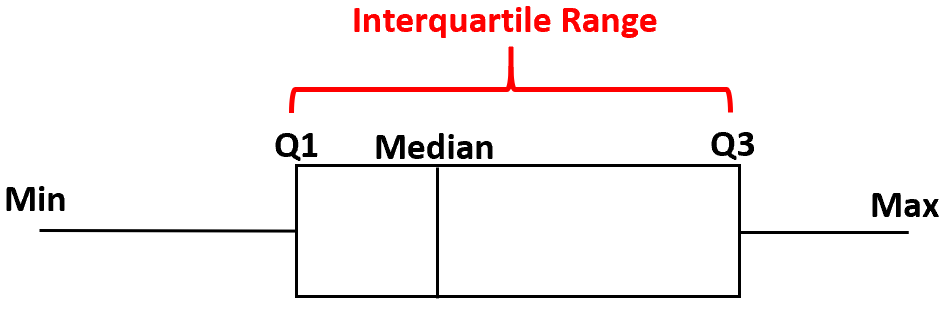
次の例は、箱ひげ図の四分位範囲 (IQR) を実際に見つける方法を示しています。
例 1: 試験結果
次の箱ひげ図は、特定の大学試験の得点の分布を示しています。テストスコアの四分位範囲はどれくらいですか?
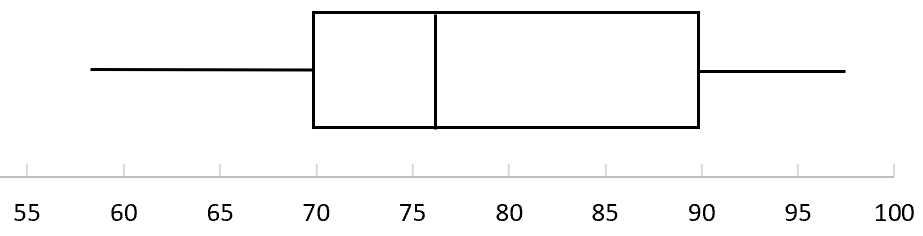
この質問に答えるために、箱ひげ図で次の値を見つけることができます。
- Q3 (上位 4 分の 1) = 90
- Q1 (下位四分位数) = 70
- 四分位スケール (IQR) = 90 – 70 = 20
検査結果の四分位範囲は20です。
例 2: 得点
次の箱ひげ図は、特定のリーグのバスケットボール選手が獲得した得点の分布を示しています。分布の四分位範囲はどれくらいですか?
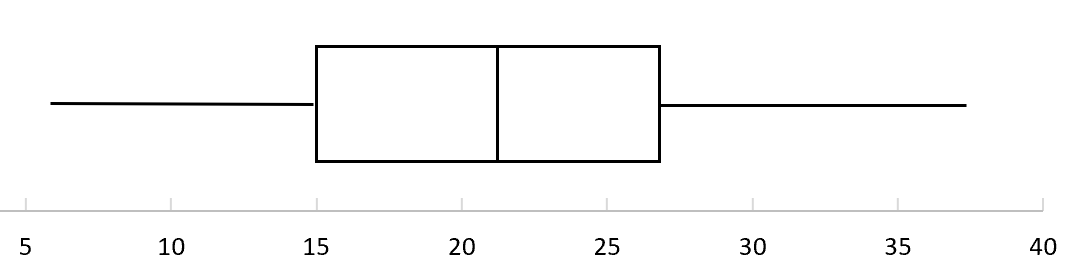
この質問に答えるために、箱ひげ図で次の値を見つけることができます。
- Q3 (上位 4 分の 1) = 27
- Q1 (下位四分位数) = 15
- 四分位スケール (IQR) = 27 – 15 = 12
分布の四分位範囲は12です。
例3:草丈の比較
次の箱ひげ図は、赤と青の 2 つの異なる植物種の高さの分布を示しています。どの分布の四分位範囲が大きいでしょうか?
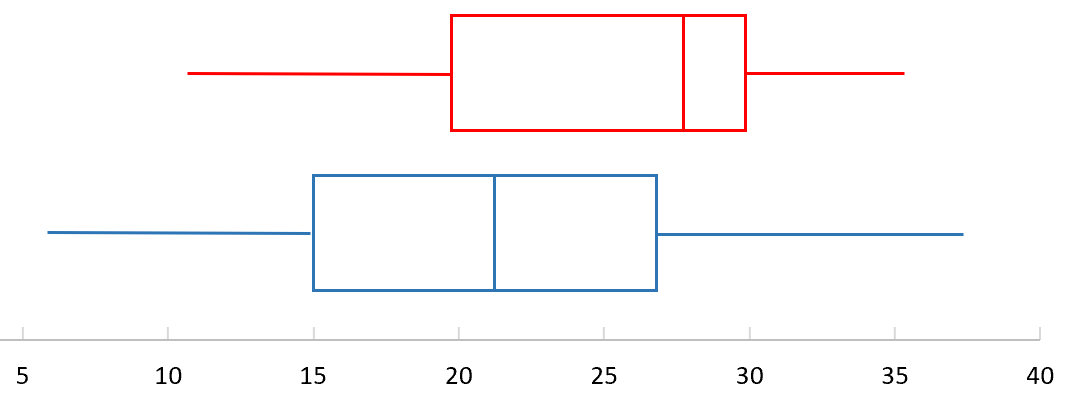
まず、赤いボックスの四分位範囲を見つけてみましょう。
- Q3 (上位 4 分の 1) = 30
- Q1 (下位四分位数) = 20
- 四分位スケール (IQR) = 30 – 20 = 10
次に、青い箱ひげ図の四分位範囲を見つけてみましょう。
- Q3 (上位 4 分の 1) = 27
- Q1 (下位四分位数) = 15
- 四分位スケール (IQR) = 27 – 15 = 12
青色種の四分位範囲はより大きくなります。
追加リソース
次のチュートリアルでは、箱ひげ図に関する追加情報を提供します。