範囲制限とは何ですか?
統計では、2 つの変数間の相関関係を測定しようとすることがよくあります。これは、次のことを理解するのに役立ちます。
- 2 つの変数間の関係の方向。 1 つの変数が増加すると、もう 1 つの変数は増加する傾向にありますか、それとも減少する傾向がありますか?
- 2 つの変数間の関係の強さ。 2 つの変数の値はどのくらい変化しますか?
残念ながら、2 つの変数間の相関を測定するときに発生する可能性のある問題は、範囲制限と呼ばれます。これは、いずれかの変数の測定値の範囲が何らかの理由で制限されている場合に発生します。
たとえば、特定の学校の生徒の学習時間と試験の成績との相関関係を測定したいとします。
学校の 1,000 人の生徒全員についてこれら 2 つの変数に関するデータを収集すると、学習時間と試験の得点との相関関係が0.73であることがわかります。
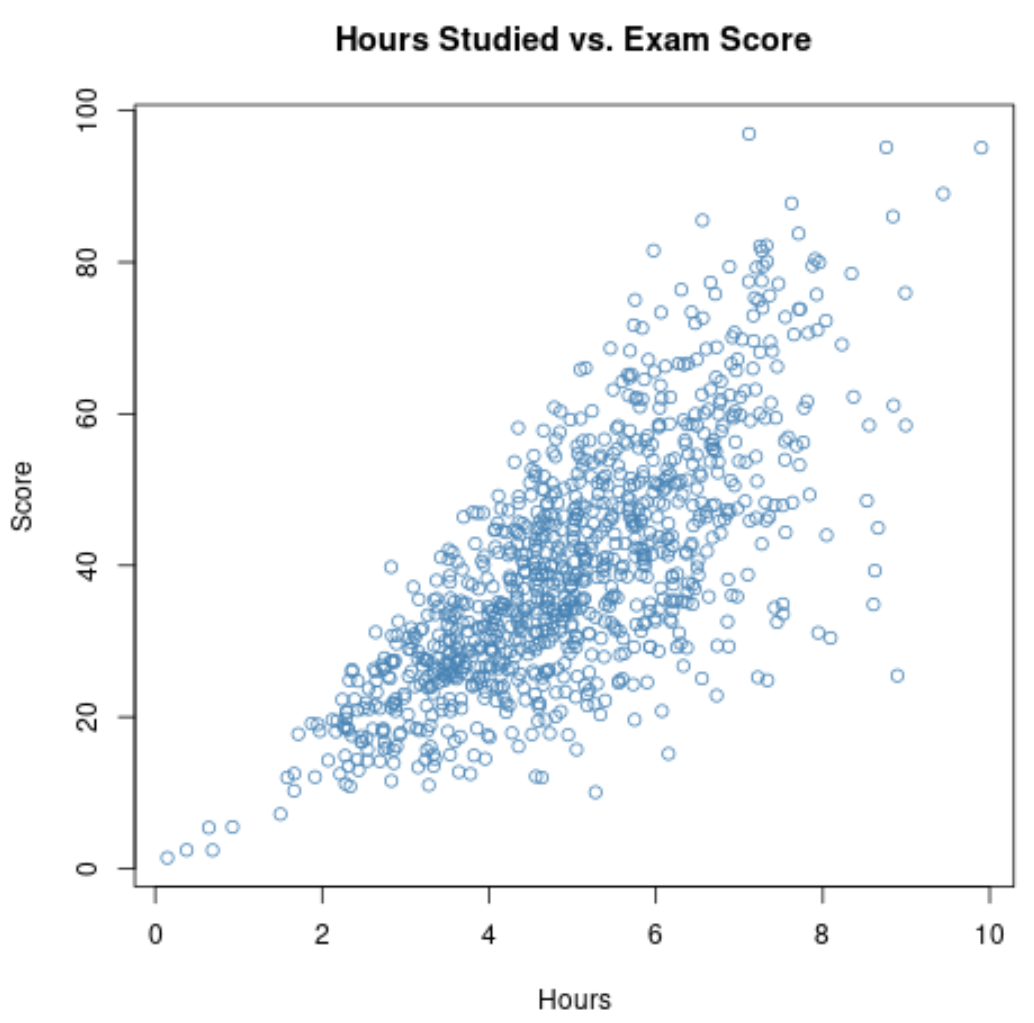
この相関関係は非常に高く、2 つの変数間に強い正の関係があることを示しています。学生は勉強すればするほど、試験の成績が良くなる傾向があります。
ただし、優等コースの学生に関するデータのみを収集すると仮定します。おそらく、これらの学生は全員、少なくとも 6 時間は勉強したことになるでしょう。
したがって、これらの生徒の学習時間と試験の得点との相関関係を計算する場合、変動する学習時間には狭い範囲を使用することになります。
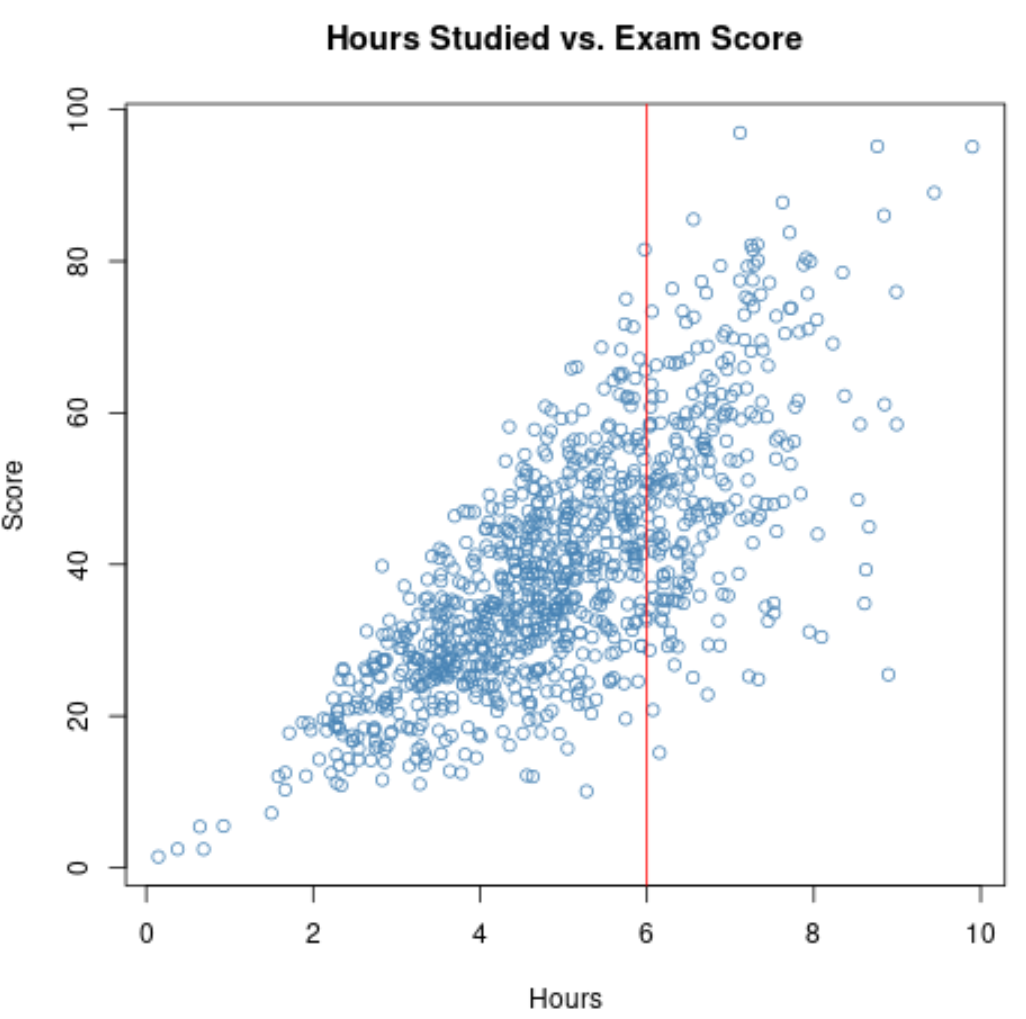
散布図で 6時間を超える範囲を拡大すると、プロットは次のようになります。
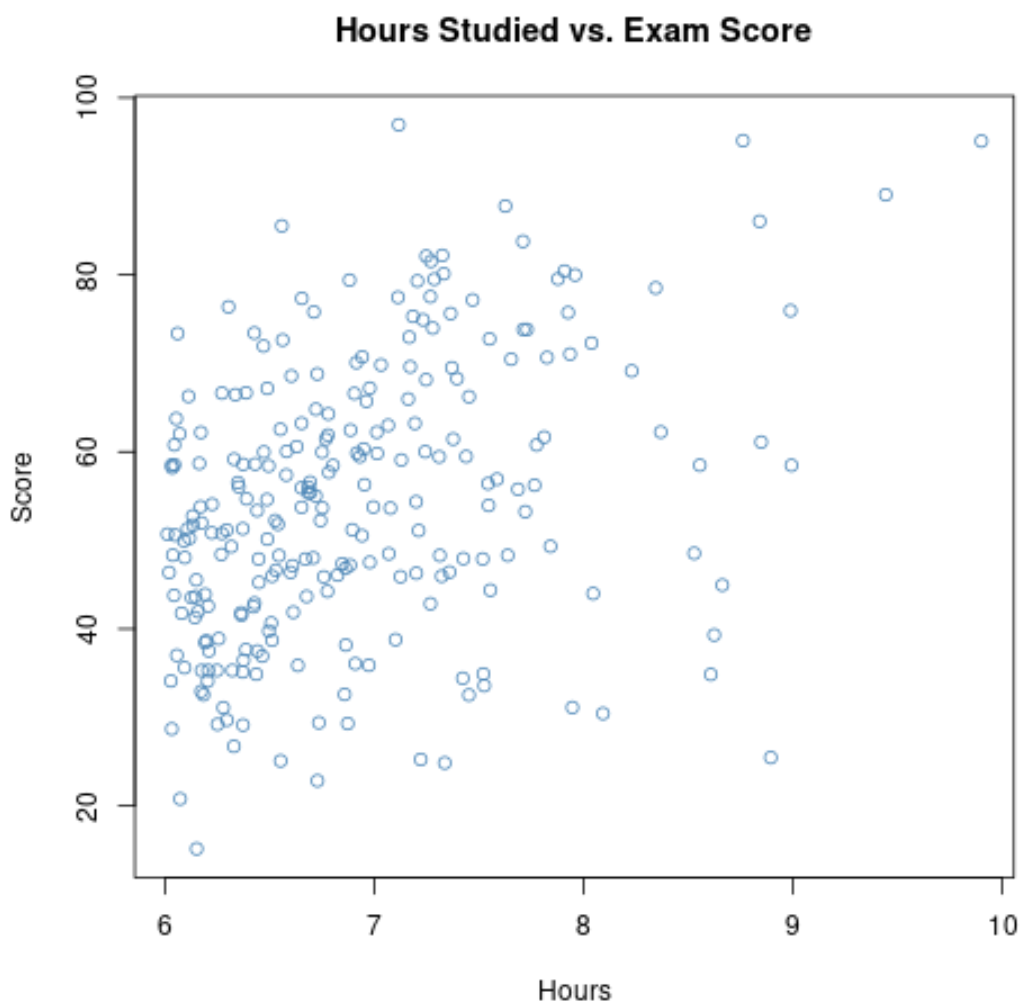
このグラフ上の 2 つの変数間の相関は0.37であることがわかり、これは0.73よりも大幅に低くなります。
したがって、優等コースの生徒の学習時間と試験の得点に関するデータのみを収集した場合、学習時間と試験の得点の間には弱い関係があると想定される可能性があります。
ただし、変数の 1 つに制限された範囲を使用したため、この結果は誤解を招く可能性があります。
範囲が制限されている実際の例
範囲が制限されているという問題は、実際にはさまざまな調査研究で発生する可能性があります。ここではいくつかの例を示します。
1. ハイパフォーマンスアスリートに関する研究。研究者は、特定のトレーニング プログラムが特定の標準プログラムよりも多くの筋肉量を生成するかどうかを研究することに興味があるかもしれません。
研究者がエリートアスリートのデータのみを収集する場合、これらのアスリートは全員、すでに高い筋肉量を持っている可能性があります。したがって、トレーニング プログラムと生成される筋肉量の相関関係を計算するために利用できる値の範囲は狭いことになります。
2. 成績優秀な学生の研究。研究者は、特定の個別指導プログラムが成績にプラスの影響を与えるかどうかを研究したいと考えるかもしれません。本質的に、成績を向上させたいと熱心に個別指導プログラムに参加している生徒は、すでに成績優秀な生徒である可能性があります。
したがって、これらの生徒の成績には改善の余地があまりないかもしれません。研究者が個別指導プログラムに費やした時間とそれによる成績上昇との相関関係を計算する場合、成績向上の余地が限られているため、真の相関関係は過小評価される可能性があります。
制限された範囲を考慮する方法
制限された範囲を説明する一般的な方法は、心理測定学者のロバート L. ソーンダイクによって開発された公式であるソーンダイク ケース 2として知られています。
この式は、2 つの変数間の真の相関関係の推定値を提供し、次の計算を使用します。
真の相関 = √(1-(SD 2 y 制限あり-SD 2 y 制限なし)) * (1-r 2制限あり)
金:
- SD 2制限付き y : 応答変数 y の利用可能なデータの二乗標準偏差。
- 無制限SD 2 y: 母集団の応答変数の既知の二乗標準偏差。
- r 2制限付き: 利用可能な制限付きデータの二次相関。
この公式は、変数の 1 つが制限された範囲の影響を受ける場合に、2 つの変数間の真の相関関係の不偏推定値を生成するのに効果的であることが示されています。
この式を使用するには、応答変数の真の母標準偏差の推定値が必要であることに注意してください。