統計に回復力があるとは何を意味するのでしょうか?

によるベンジャミン・アンダーソン博士 7月 24, 2023 ガイド 0コメント

統計が極端な値に敏感でない場合、その統計は回復力があると言われます。

以下に、回復力のある統計の 2 つの例を示します。

以下に、維持できない統計の例を示します。

次の例は、復元力のある統計と復元力のない統計の違いを示しています。

次のデータセットがあるとします。

データセット: 2、5、6、7、8、13、15、18、22、24、29

電卓または統計ソフトウェアを使用すると、このデータセットの次の保持統計の値を計算できます。

このデータセットの次の非回復性統計の値を計算することもできます。

ここで、このデータセットに極端な外れ値が追加されているかどうかを考えてみましょう。

データセット: 2、5、6、7、8、13、15、18、22、24、29、450

このデータセットの次の復元統計の値を再度計算できます。

このデータセットの次の非回復性統計の値を計算することもできます。

データセットに極値を追加するだけで、非抵抗統計がどれだけ変化するかに注目してください。

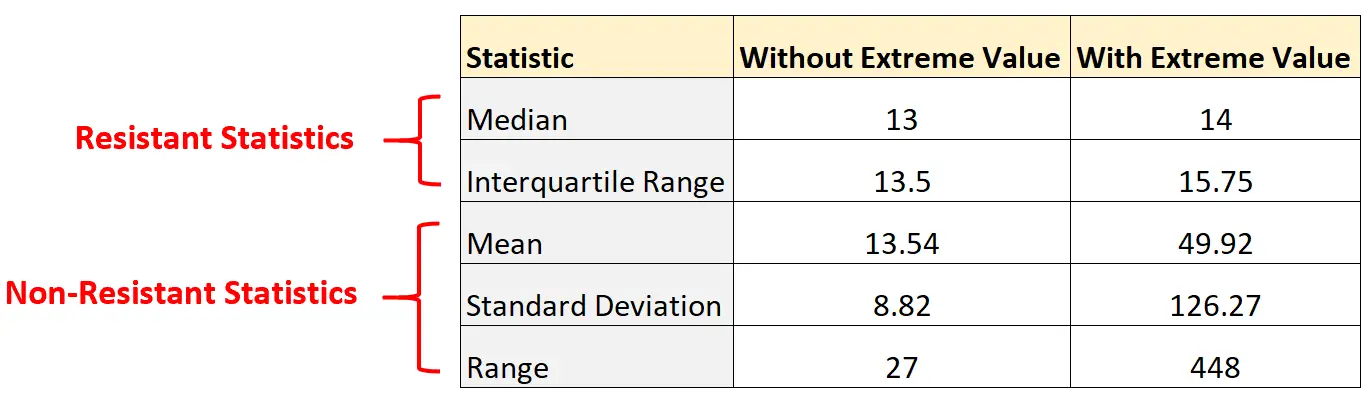
抵抗統計の例

逆に、レジスタンス戦士の統計はほとんど変わっていない。中央値と四分位範囲はわずかに変化しました。

データセット内の値の中心と分散を測定するために最も一般的に使用される統計は、それぞれ平均と標準偏差です。

残念ながら、これらの統計はどちらも極端な値に敏感です。したがって、データセットに外れ値が存在する場合、平均と標準偏差はデータセット内の値の分布を正確に表すことができません。

代わりに、外れ値が存在する場合は、中央値と四分位範囲を使用してデータセット内の値の中心と分散を測定することをお勧めします。これらの統計は両方とも堅牢であるためです。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る