統計におけるランダム化: 定義と例
統計学の分野では、ランダム化とは、研究対象を異なる治療グループにランダムに割り当てる行為を指します。
たとえば、研究者が 2 つの異なる錠剤が血圧に異なる影響を与えるかどうかを理解したいという研究に参加する 100 人の被験者を募集したとします。
彼らは、乱数発生器を使用して、錠剤 #1 または錠剤 #2 を使用するように各被験者をランダムに割り当てることを決定する場合があります。
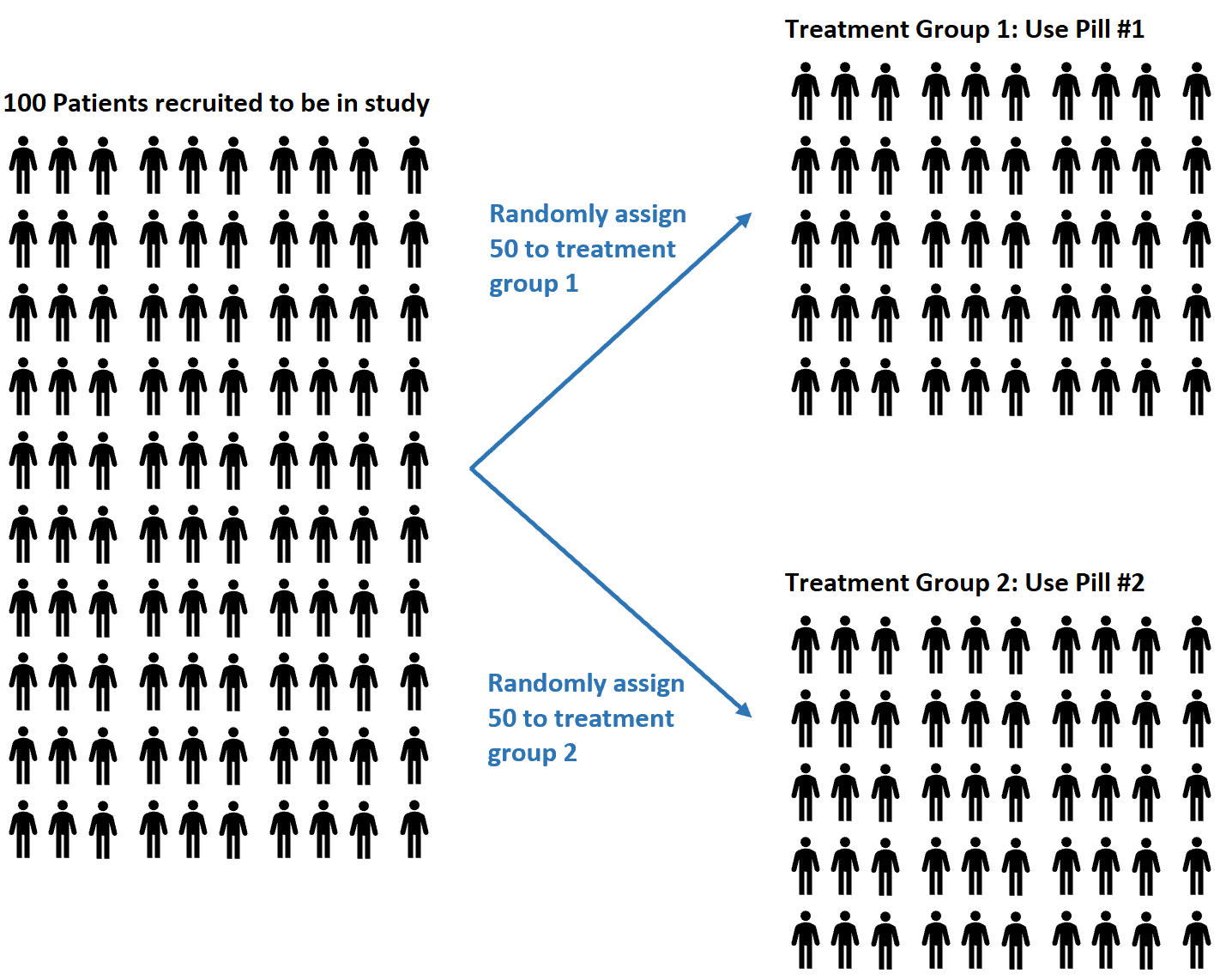
ランダム化の利点
ランダム化の目的は、隠れた変数、つまり分析に直接含まれないが、何らかの形で分析に影響を与える変数を制御することです。
たとえば、研究者が血圧に対する 2 つの異なる錠剤の影響を研究する場合、次の隠れた変数が分析に影響を与える可能性があります。
- タキシードの服
- ダイエット
- エクササイズ
被験者を治療グループにランダムに割り当てることで、隠れた変数が両方の治療グループに同等に影響を与える可能性を最大化します。
これは、血圧の違いは、隠れた変数の影響ではなく、錠剤の種類に起因する可能性があることを意味します。
ブロックのランダム化
ランダム化の拡張は、ブロック ランダム化として知られています。これは、最初に被験者をブロックに分割し、次にランダム化を使用してブロック内の被験者を異なる治療に割り当てるプロセスです。
たとえば、研究者が 2 つの異なる錠剤が血圧に異なる影響を与えるかどうかを知りたい場合、まずすべての被験者を性別 (男性または女性) に基づいて 2 つのブロックに分けることができます。
次に、各ブロックでランダム化を使用して、錠剤 #1 または錠剤 #2 のいずれかを使用するよう被験者をランダムに割り当てます。
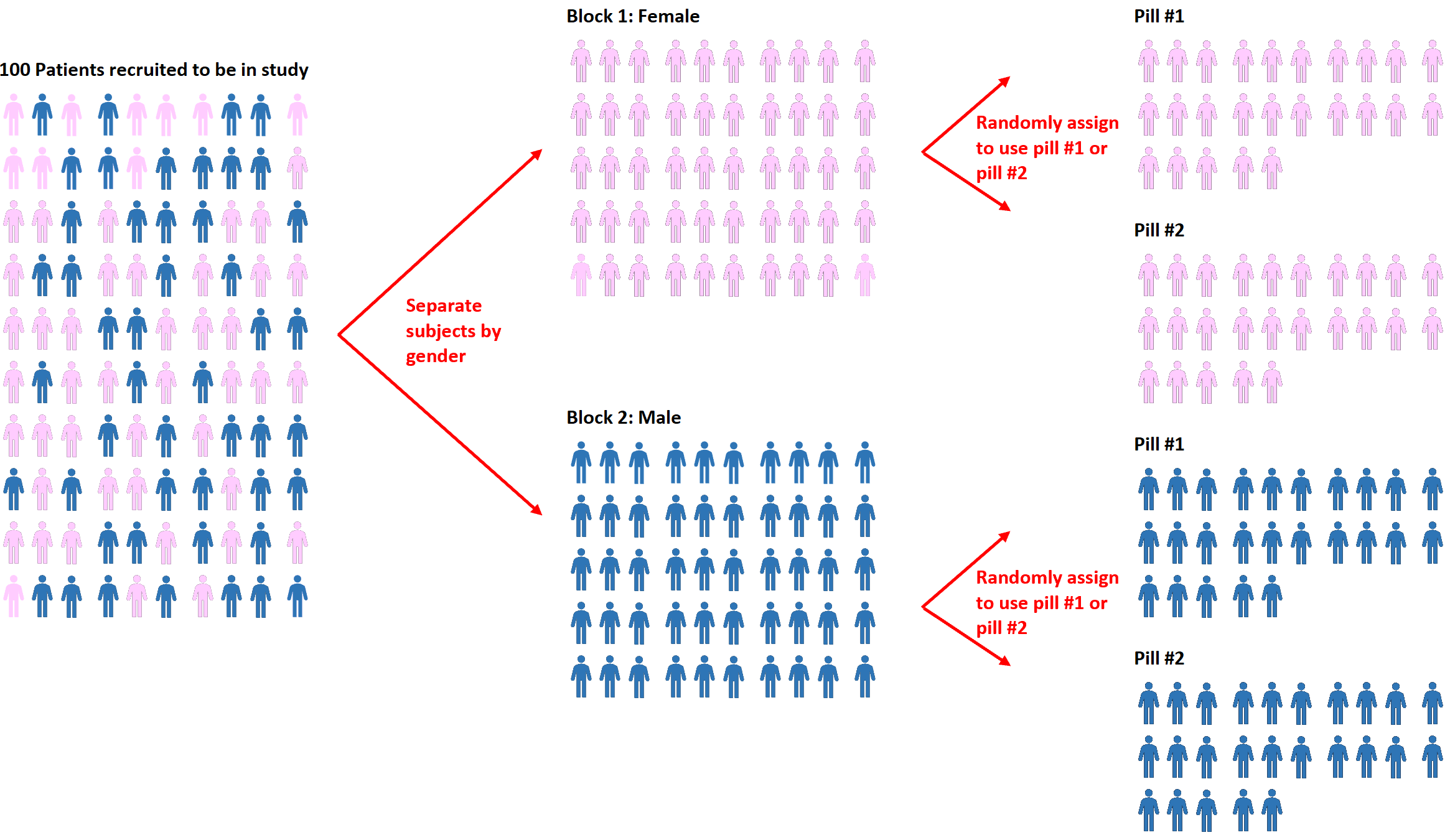
このアプローチの利点は、男性と女性では各錠剤に対する反応が異なる可能性が高いことがわかっているため、研究者が性別が血圧に与える影響を直接制御できることです。
性別をブロックとして使用することで、変動の潜在的な原因としてこの変数を排除することができます。 2 つの錠剤間に血圧に差がある場合、性別がその差の根本的な原因ではないことがわかります。