統計サンプル

この記事では、統計サンプルとは何か、またその使用目的について説明します。また、母集団とサンプルの概念の違いや、統計サンプルのいくつかの例も確認できます。さらに、サンプルが代表的であるために備えなければならない特性も示します。

統計サンプルとは何ですか?

統計サンプルは、統計母集団からの個人のグループです。言い換えれば、統計学におけるサンプルとは、統計調査が実行される母集団の一部です。

たとえば、選挙調査が実施される場合、統計サンプルは質問されたすべての人々から構成されます。

通常、研究をしようと思ったとき、研究会を構成するすべての要素を研究することはできません。前の例と同様に、選挙で投票した人全員を検査することは不可能です。したがって、通常は研究グループの一部のみを分析し、その結果をグループ全体に推定するためにサンプルが選択されます。

これは統計的推論によって実現できます。これにより、標本結果から母集団パラメータを非常に小さな誤差で決定できるようになります。

サンプルと母集団

統計学において、母集団とは、統計調査の実行対象となる類似の特性を持つ要素のセットです。この概念は、統計的母集団または単に母集団と呼ばれることがあります。

統計サンプルと統計母集団の違いは、研究の要素の総数に対する割合です。これは、サンプルが母集団の一部であり、分析対象のグループを構成するすべての要素を表すためです。

したがって、サンプルのサイズは常に母集団のサイズ以下になります。

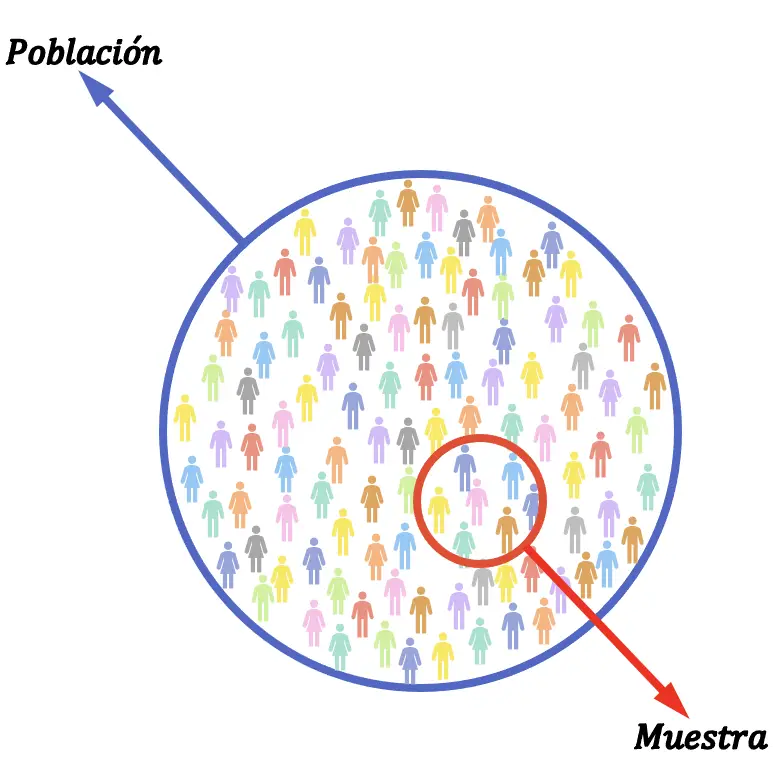
たとえば、工場で生産された不良部品の割合について統計的調査を行いたい場合、製造されたすべての部品を調査するのではなく、ランダムに選択した部品のセットのみを調査します。したがって、この場合、母集団は工場で生産された部品で構成され、一方、サンプルは統計研究で分析されたすべての部品です。

統計調査を実行するために選択されたサンプルが母集団の特徴を代表するものであることが重要です。そうすることで、サンプルから引き出された結論を母集団全体に当てはめることができます。次に、サンプルから個人を選択する方法を見ていきます。

サンプルとサンプリング

統計学におけるサンプリングは、母集団からサンプルを選択するプロセスです。言い換えれば、サンプリングは、統計調査を実行するために個人のグループを選択する方法です。

たとえば、サンプリングを行う 1 つの方法は、個人をランダムに選択することです。したがって、統計的母集団のサイズを研究したい場合は、単純なランダムサンプリングによって研究サンプルを選択できます。

母集団を抽出するにはいくつかの方法があり、それぞれに長所と短所があります。さまざまな種類の統計サンプリングがどのようなものかを確認するには、次のリンクをクリックしてください。

サンプルサイズ

サンプル サイズ(またはサンプル サイズ) は、研究のサンプルを構成する個人の数です。統計では、サンプルが母集団全体を代表するようにサンプル サイズが重要です。

たとえば、国の標高を分析したい場合、その国の全住民の身長を尋ねることはできません。調査には時間がかかり、費用もかかりすぎるからです。したがって、無作為抽出を実施し、母集団の代表的なサンプルのみにインタビューする必要があります。

ただし、統計研究のサンプル サイズは、母集団全体の特性を表すのに十分な大きさでなければなりません。一方で、研究の費用が高くなるため、サンプルサイズを過度に大きくすることはできません。したがって、サンプルサイズは大きすぎず、小さすぎず、適切である必要があります。適切なサンプル サイズを計算する方法はここで確認できます。

代表的なサンプル

統計において、代表サンプルとは、母集団内の個人を適切に表すサンプルのことです。言い換えれば、代表サンプルは、それが代表する母集団の特徴と類似した特徴を持つ母集団の一部です。

得られた結果を母集団全体に適用できるように、統計調査のサンプルが代表的なものであることが重要です。研究されたサンプルが代表的でない場合、母集団と一致しない結果が得られるため、誤った結論が導き出されることになります。

代表的なサンプルを取得する方法は、ランダムな個人グループの選択に基づくことはできませんが、サンプルの代表性は、サンプリング方法、サンプルのサイズ、誤差の範囲、信頼水準、等

まず、適切なサンプリング手法を使用して、代表的なサンプルを取得する必要があります。サンプリングにはいくつかの種類があり、それぞれがサンプルの種類に適しているため、母集団の特性に応じて、いずれかのサンプリング手法を使用することが望ましいです。

次のリンクでは、さまざまなタイプのサンプリングが何であるか、および各状況にどのタイプのサンプリングが最適であるかを確認できます。

さらに、サンプリングエラーを避ける必要があります。標本誤差とは、標本を取得する過程で生じる誤差であり、その結果、標本と母集団の特性が異なってしまいます。したがって，標本データから母集団パラメータを推定することは誤りです。したがって、サンプリングプロセスと選択したサンプリング方法の両方に注意を払う必要があります。

第二に、代表的なサンプルは適切なサイズでなければなりません。標本が母集団の特性を表すには、標本内の観測値の数が十分に大きくなければなりません。一方で、調査費用が高すぎるため、サンプルサイズをあまり大きくすることはできません。つまり、理想的なサンプル サイズを選択するには、代表性とサンプル コストの間でバランスを取る必要があります。

統計におけるサンプルの利点

最後に、母集団全体ではなくサンプルを研究することの利点をまとめて見てみましょう。

• サンプルのみを調べると、調査する必要がある個人の数が少なくなるため、統計的調査が容易になります。
• データ収集にかかる費用が少なくなるため、研究の経済的コストが削減されます。
• これにより、収集する必要のあるデータが少なくなるため、調査をより迅速に実施できます。
• 集団内のすべての個人を分析する必要がある場合には実行不可能な統計研究を実行できるようになります。