統計式

による 8月 1, 2023 統計 0コメント

ここでは主な統計式を紹介します。また、各統計式の適用例を確認できる記事へのリンクも残しておきます。さらに、計算を実行して式の結果を直接知る必要がないように、オンライン計算機を使用することもできます。

中心傾向の統計的尺度の公式

半分

平均を計算するには、すべての値を加算し、データの総数で割ります。したがって、平均の式は次のようになります。

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}

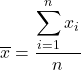
統計学では、平均は算術平均または平均とも呼ばれます。

中央値

中央値は、すべてのデータを最小値から最大値の順に並べた中央の値です。言い換えれば、中央値は順序付けされたデータセットを 2 つの等しい部分に分割します。

中央値の計算は、データの総数が偶数か奇数かによって異なります。

  • データの総数が奇数の場合、中央値はデータの中央に位置する値になります。つまり、ソートされたデータの位置 (n+1)/2 にある値です。

    • Me=x_{\frac{n+1}{2}

  • データ ポイントの合計数が偶数の場合、中央値は中央に位置する 2 つのデータ ポイントの平均になります。つまり、順序付けされたデータの位置 n/2 および n/2+1 で見つかる値の算術平均です。

    • Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}

金

n

はサンプル内のデータの総数であり、記号Me は中央値を示します。

ファッション

統計において、最頻値はデータ セット内で最も高い絶対頻度を持つ値、つまり、最頻値はデータ セット内で最も繰り返される値です。

したがって、最頻値を表す特定の公式はありませんが、統計データセットの最頻値を計算するには、サンプル内で各データ要素が出現する回数を数えるだけで、最も多く繰り返されたデータが最頻値となります。

モードは、統計モードまたは最頻値とも言えます。

分散の統計的尺度の公式

標準偏差

標準偏差は、標準偏差とも呼ばれ、データ系列の偏差の二乗和の平方根を観測値の総数で割ったものに等しくなります。

したがって、標準偏差の式は次のようになります。

\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}

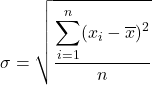
分散

分散は、観測値の総数に対する残差の二乗の合計に等しくなります。したがって、この統計指標の式は次のようになります。

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}

金：

  • X

    分散を計算する確率変数です。

  • x_i

    データ値です

    i

    。

  • n

    観測値の合計数です。

  • \overline{X}

    確率変数の平均です

    X

    。

変動係数

統計学において、変動係数は、平均に対するデータセットの分散を決定するために使用される分散の尺度です。変動係数は、データの標準偏差をその平均で割った後、100 を掛けて値をパーセンテージで表すことによって計算されます。

CV=\cfrac{\sigma}{\overline{x}}\cdot 100

きちんとした

統計範囲は、サンプル内のデータの最大値と最小値の差を示す分散の尺度です。したがって、母集団または統計サンプルの範囲を計算するには、最小値から最大値を減算する必要があります。

R=\text{M\'ax}-\text{M\'in}

四分位範囲

四分位範囲 は、四分位範囲とも呼ばれ、第 3 四分位数と第 1 四分位数の差を示す統計的分散の尺度です。

したがって、統計データ セットの四分位範囲を計算するには、まず第 3 四分位数と第 1 四分位数を見つけてから、それらを減算する必要があります。

IQR=Q_3-Q_1

中程度の差

平均偏差 は、平均絶対偏差とも呼ばれ、絶対偏差の平均です。したがって、平均偏差は、算術平均からの各データ項目の偏差の合計をデータ項目の総数で割ったものに等しくなります。

D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}

統計的位置測定の公式

四分位数

統計において、四分位とは、順序付けされたデータのセットを 4 つの等しい部分に分割する 3 つの値です。したがって、第 1 四分位、第 2 四分位、および第 3 四分位は、それぞれ、すべての統計データの 25%、50%、および 75% を表します。

四分位は大文字の Q と四分位インデックスで表されるため、最初の四分位は Q 1 、2 番目の四分位は Q 2 、そして 3 番目の四分位は Q 3となります。

四分位数式は次のとおりです。

\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3

注:この式は、四分位の値ではなく、四分位の位置を示します。四分位は計算式で求めた位置にあるデータとなります。

ただし、この式の結果から 10 進数が得られる場合があります。したがって、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

  • 式の結果が小数部のない数値である場合、四分位は上記の式で指定された位置にあるデータです。
  • 数式の結果が小数部を含む数値である場合、四分位値は次の数式を使用して計算されます。

Q=x_i+d\cdot (x_{i+1}-x_i)

ここで、x iおよびx i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

十分位数

統計において、十分位数とは、順序付けされたデータのセットを 10 等分する 9 つの値です。したがって、1 位、2 位、3 位、… はサンプルまたは母集団の 10%、20%、30% を表します。

十分位数は大文字 D と十分位数インデックスで表されます。つまり、最初の十分位数は D 1 、2 番目の十分位数は D 2 、3 番目の十分位数は D 3などとなります。

十分位数の式は次のとおりです。

\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9

注意:この式は、十分位の値ではなく、十分位の位置を示します。十分位数は、式で求めた位置にあるデータとなります。

ただし、この式の結果が 10 進数になる場合があるため、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

  • 式の結果が小数部を除いた数値の場合、十分位は上記の式で指定された位置にあるデータです。
  • 式の結果が小数部を含む数値である場合、十分位値は次の式を使用して計算されます。

D=x_i+d\cdot (x_{i+1}-x_i)

ここで、x iおよびx i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

パーセンタイル

統計において、パーセンタイルは、順序付けされたデータのセットを 100 等分に分割する値です。したがって、パーセンタイルは、データセットのパーセンテージが下回る値を示します。

パーセンタイルは大文字 P とパーセンタイル インデックスで表されます。つまり、最初のパーセンタイルは P 1 、40 番目のパーセンタイルは P 40 、79 番目のパーセンタイルは P 79などとなります。

パーセンタイルの式は次のとおりです。

\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99

注意:この式はパーセンタイルの位置を示しますが、その値は示しません。パーセンタイルは、式で求めた位置にあるデータとなります。

ただし、この式の結果が 10 進数になる場合があるため、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

  • 数式の結果が小数部を除いた数値である場合、パーセンタイルは上記の数式で指定された位置にあるデータに対応します。
  • 式の結果が小数部を含む数値の場合、正確なパーセンタイル値は次の式を使用して計算されます。

P=x_i+d\cdot (x_{i+1}-x_i)

ここで、x iおよびx i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

統計的形状測定式

非対称係数

歪度係数または歪度指数は、分布の歪度を決定するために使用される統計係数です。したがって、非対称係数を計算すると、分布をグラフで表現しなくても、分布の非対称の種類を知ることができます。

非対称係数の式は次のとおりです。

\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}

同様に、次の 2 つの公式のいずれかを使用して、フィッシャーの非対称係数を計算できます。

\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}

\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}

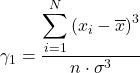
金

E

は数学的な期待値であり、

\overline{x}

算術平均、

\sigma

標準偏差と

n

データの総数。

➤参照:非対称係数

尖度係数

尖度はシャープネスとも呼ばれ、分布が平均値付近にどの程度集中しているかを示します。言い換えれば、尖度は分布が急峻であるか平坦であるかを示します。具体的には、分布の尖度が大きいほど、分布は急峻になります (または鋭くなります)。

尖度係数の式は次のとおりです。

\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3

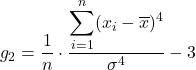
金

x_i

観測値に対応する値です

i

、

\overline{x}

算術平均、

\sigma

標準偏差と

n

データの総数。

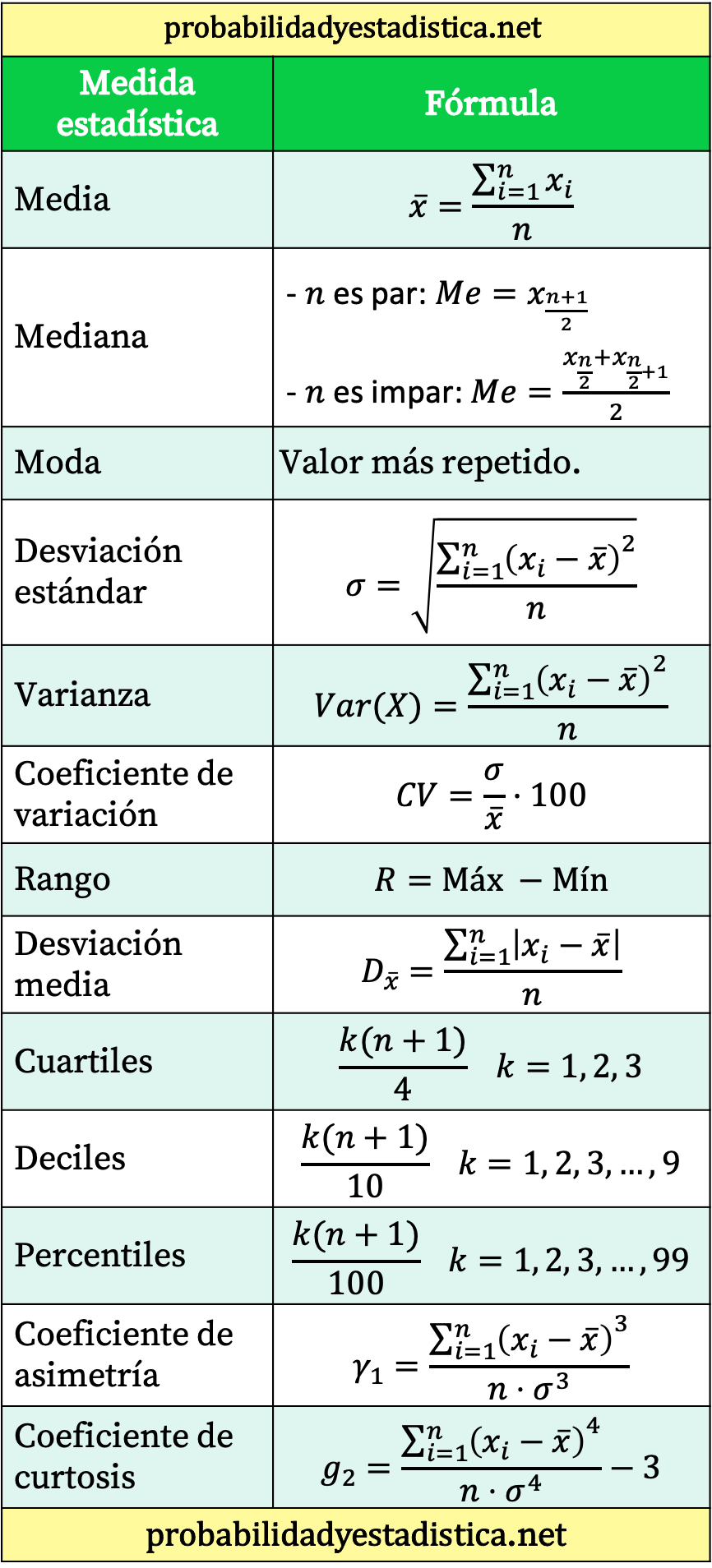
全統計式のまとめ表

最後に、主な統計式をまとめた表を示します。

統計式
➤参照:確率の公式

著者について

Dr. Benjamin Anderson
ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る

コメントを追加する

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です