Socs: ディストリビューションを説明する便利な頭字語
統計では、一連のデータがどのように分布しているかを理解したいことがよくあります。特に、ディストリビューションについて知っておくと役立つことが 4 つあります。
1 .形
- 分布は対称的ですか、それとも片側に偏っていますか?
- 分布は単峰性 (1 つのピーク) ですか、それとも二峰性(2 つのピーク) ですか?
2. 外れ値
- 分布に異常値はありますか?
3. センター
- 平均値、中央値、分布様式は何ですか?
4.スプレッド
- 分布の範囲、四分位範囲、標準偏差、分散はどれくらいですか?
SOCS は、これら 4 つのことを覚えるために使用できる便利な頭字語です。 「形状、外れ値、中心、広がり」を意味します。
SOCS を使用してディストリビューションを記述する方法の簡単な例を見てみましょう。
例: SOCS を使用してディストリビューションを記述する方法
20 種類の異なる植物のサンプルの高さを示す次のデータセットがあるとします。
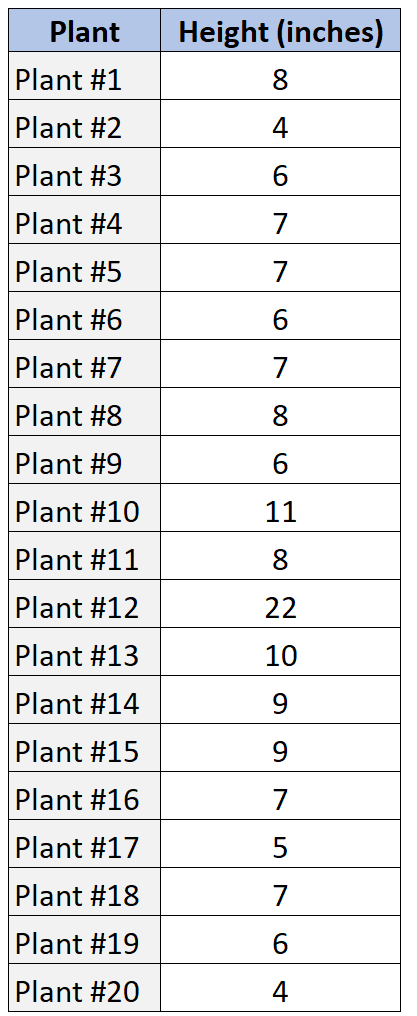
SOCS を使用してこのデータ値の分布を記述する方法を次に示します。
形
まず、分布の形状について説明します。
分布の形状を視覚化する便利な方法は、データ セット内の各値の頻度を表示するヒストグラムを作成することです。
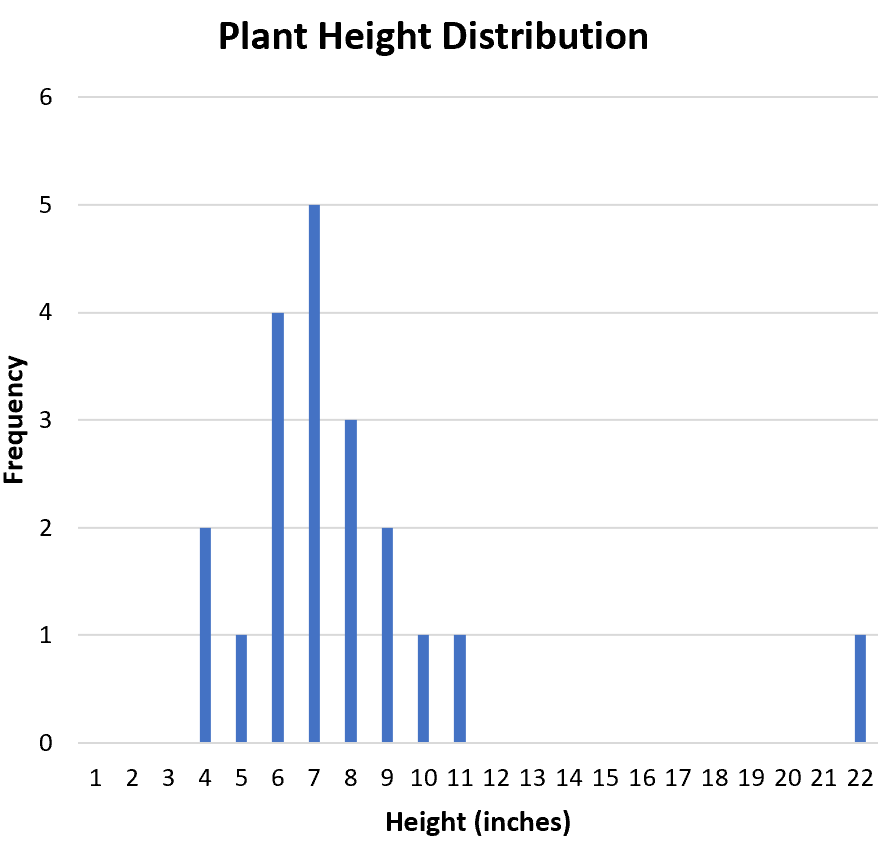
分布は対称的ですか、それとも片側に偏っていますか? ヒストグラムから、分布がほぼ対称であることがわかります。つまり、価値観がどちらかに偏ることはないのです。
分布は単峰性 (1 つのピーク) ですか、それとも二峰性 (2 つのピーク) ですか?分布は単峰性です。値「7」にピークがあります。
外れ値
次に、データセットに外れ値があるかどうかを判断します。ヒストグラムから分布を視覚的に検査し、22 が外れ値である可能性があることを確認できます。
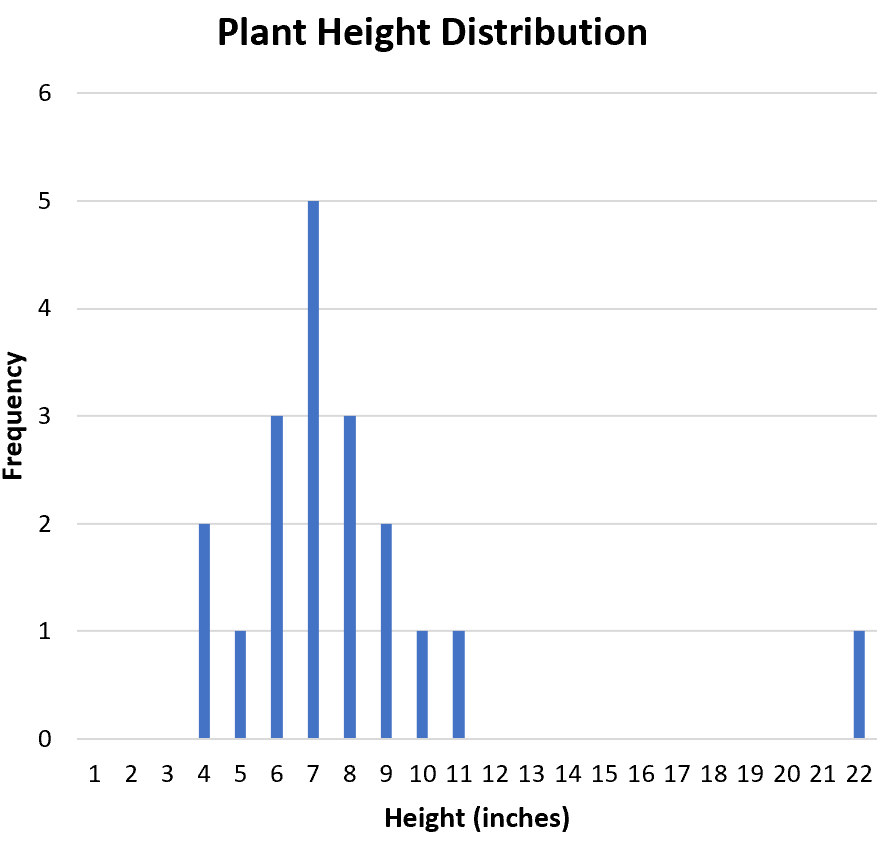
外れ値を正式に定義する一般的な方法は、第 3 四分位以上または第 1 四分位以下の四分位範囲の 1.5 倍の値です。
四分位範囲計算ツールを使用すると、20 個の生データ値を入力すると、第 3 四分位が9 、四分位範囲が3であることがわかり、したがって 9 + (1.5*3) = 13.5より大きい値は外れ値になります。定義により。
22 は 13.5 より大きいため、22 は外れ値であると宣言できます。
中心
次に、分布の中心がどこにあるかを説明します。使用できる中心傾向の 3 つの一般的な尺度は、平均、中央値、最頻値です。
平均:これは分布の平均値です。これは、すべての個々の値を合計し、値の合計数で割ることで求められます。
平均 = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85
中央値:これは分布の「平均」値です。これは、すべての値を最小から最大の順に並べ、中央値を特定することでわかります。それは7であることがわかります。
4、4、5、6、6、6、6、7、7、7、7、7、8、8、8、9、9、10、11、22 _
モード:これは最も頻繁に表示される値です。それは7であることがわかります。
広める
次に、分布における値の分布について説明します。使用できる分散の 4 つの一般的な尺度は、範囲、四分位範囲、標準偏差、分散です。
範囲:これは、データセット内の最大値と最小値の差です。これは、 22 – 4 = 18となります。
四分位範囲:データ値の中央の 50% の幅を測定します。 20 個の生データ値を四分位範囲計算ツールに入力すると、これが3に等しいことがわかります。
標準偏差:これは、データ値の平均分布の尺度です。 20 個の生データ値を分散および標準偏差の計算ツールに入力すると、標準偏差が3.69に等しいことがわかります。
分散:これは単純に標準偏差の 2 乗です。これは 3.69 2 = 13.63に等しくなります。
結論
SOCS をガイドとして使用すると、草丈分布を次のように記述することができました。
- 分布は単峰性かつ対称的でした。つまり、ピークが 1 つだけあり、どちらかの側に偏っていませんでした。
- 分布には外れ値が 1 つありました: 22。
- 分布の平均は 7.85、中央値は 7、最頻値は 7 でした。
- 分布の範囲は 18、四分位範囲は 3、標準偏差は 3.69、分散は 13.63 でした。
SOCS を使用して任意の分布を記述することができることに注意してください。これは、分布の形状、異常値の有無、ほぼ中心がどこにあるのか、値データの分布方法を完全に理解するのに便利な方法です。は。