絶対周波数

この記事では、統計における絶対頻度の意味について説明します。したがって、データセットの絶対頻度を取得する方法、2 つの演習を解決し、さらに他のタイプの統計頻度との違いを理解します。

絶対周波数とは何ですか?

統計において、絶対頻度とは、データセット内に値が出現する回数です。簡単に言えば、絶対頻度は結果が繰り返される回数です。

たとえば、アンケートに参加した 7 人が自分の好きな色は赤であると答えた場合、赤の絶対頻度は 7 になります。

したがって、すべての値の絶対頻度の合計は、統計サンプル内のデータの総数に等しくなります。

一般に、下付き文字iが付いた文字fは、値iの絶対周波数を表すために使用されるため、絶対周波数の記号は_fiになります。

絶対周波数の計算方法

データセットの絶対周波数を取得するには、次の手順に従う必要があります。

1. 変数が離散型の場合は、データセットに表示されるすべての異なる値の配列を作成します。つまり、それぞれの異なる値をテーブルの行に配置します。
2. 変数が連続の場合は、データを間隔にグループ化し、すべての間隔を含むテーブルを作成します。
3. データセット内に値が出現する回数を数え、結果を度数表に記録します。
4. サンプル データの異なる値ごとに前の手順を繰り返します。

絶対周波数の例

絶対周波数の定義とその計算方法の理論を理解したら、その計算方法を理解するために 2 つの例を見ていきます。最初の例では離散変数の絶対周波数を決定し、2 番目の例では連続変数の絶対頻度を決定します。これは、手順が場合によって若干異なるためです。

例 1: 離散変数

• 30人クラスの統計で得られた点数は以下の通りです。各音符の絶対周波数はいくらですか?

この場合、整数のみが存在できるため、離散変数になります。そのため、整数を間隔にグループ化する必要はありません。

したがって、各値が出現する回数を数えて、頻度表に書き込むだけです。

すべての絶対周波数の合計がデータ ポイントの総数に等しいことに注意してください。このルールに従わない場合は、一部のデータを数え忘れたことを意味します。

例 2: 連続変数

• 20名の身長を測定したところ、以下の結果が得られました。データを間隔に分割し、各間隔の絶対頻度を求めます。

数値は小数になる可能性があるため、このサンプルのデータは連続分布に従います。したがって、データを間隔にグループ化する必要があります。この場合は、10 分の 1 の幅で間隔を作成します。

したがって、各間隔のデータ数を数え、絶対頻度を表に表します。

絶対頻度と累積絶対頻度

名前が示すように、累積絶対頻度は統計で使用される別のタイプの頻度であり、絶対頻度に関連します。

値の累積絶対頻度は、値自体の絶対頻度と以前のすべての値の絶対頻度の合計に等しくなります。

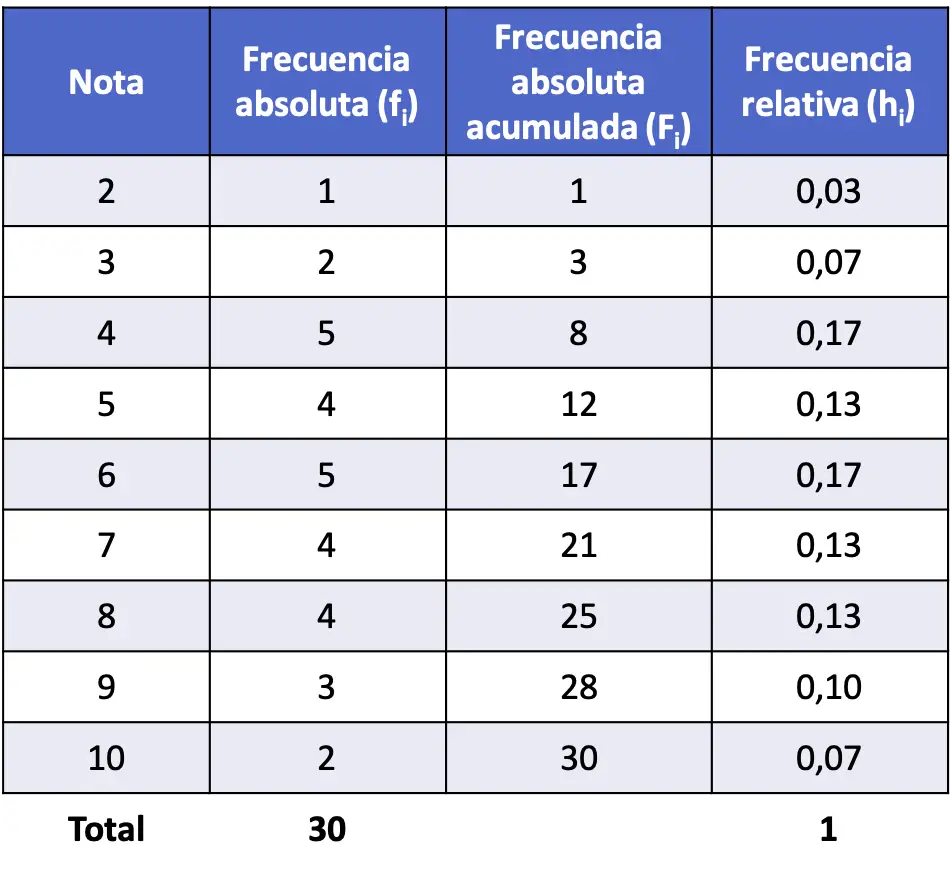
例として、上記で解決した最初の演習の累積絶対周波数の計算を以下に示します。

絶対周波数と相対周波数

統計において、相対頻度は、全体に対する各値の割合を表すため、上記の 2 つの頻度とは異なるタイプの頻度です。このため、このセクションでは、これら 2 つの概念の違いについて説明します。

絶対頻度と相対頻度の違いは、絶対頻度はサンプル内の値の絶対数であるのに対し、相対頻度は合計に対する各値の割合であることです。

したがって、相対頻度は、絶対頻度をデータの総数で割ることによって計算されます。