単線形回帰の概要

単純線形回帰は、 2 つの変数 x と y の間の関係を理解するために使用できる統計手法です。

変数xは、予測変数として知られています。

もう 1 つの変数yは、応答変数として知られています。

たとえば、7 人の個人の体重と身長を含む次のデータセットがあるとします。

体重を予測変数、身長を応答変数としましょう。

これら 2 つの変数を、X 軸に体重、Y 軸に身長をとって散布図を使用してグラフ化すると、次のようになります。

体重と身長の関係を理解したいとします。散布図から、体重が増加すると身長も増加する傾向があることがはっきりとわかりますが、この体重と身長の関係を実際に定量化するには、線形回帰を使用する必要があります。

線形回帰を使用すると、データに最もよく「適合」する直線を見つけることができます。この直線は最小二乗回帰直線として知られており、体重と身長の関係を理解するのに役立ちます。

通常、この直線の方程式を見つけるには、Microsoft Excel、SPSS、またはグラフ電卓などのソフトウェアを使用します。

最適な直線の式は次のように記述されます。

ŷ = b ₀ + b ₁ x

ここで、ŷ は応答変数の予測値、b ₀は切片、b ₁は回帰係数、x は予測変数の値です。

関連: 現実の生活で線形回帰を使用する 4 つの例

「最適なライン」を見つける

この例では、 統計線形回帰計算ツールにデータを入力して、 Calculateを押すだけです。

計算機は自動的に最小二乗回帰直線を見つけます。

ŷ = 32.7830 + 0.2001x

前の散布図からズームアウトして、この線をグラフに追加すると、次のようになります。

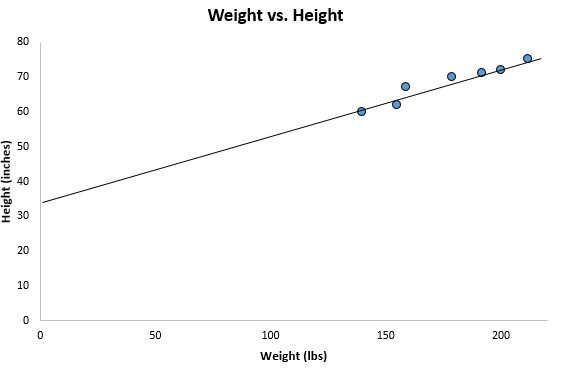
データ ポイントがこの線の周囲に密集して分散していることに注目してください。実際、この最小二乗回帰直線は、描画できるすべての直線の中でデータに最も適した直線です。

最小二乗回帰直線を解釈する方法

この最小二乗回帰直線の解釈方法は次のとおりです: ŷ = 32.7830 + 0.2001x

_b0 = 32.7830 。これは、予測変数の重量が 0 ポンドの場合、予測される身長は 32.7830 インチであることを意味します。 b ₀の値を知ると役立つ場合がありますが、この特定の例では、人の体重がゼロポンドであることはできないため、b ₀を解釈することは意味がありません。

_b1 = 0.2001 。これは、 xの 1 単位の増加はyの 0.2001 単位の増加に関連することを意味します。この場合、体重が 1 ポンド増加すると、身長が 0.2001 インチ増加します。

最小二乗回帰直線の使い方

この最小二乗回帰直線を使用すると、次のような質問に答えることができます。

体重が 170 ポンドの人の場合、身長はどのくらいだと予想すべきでしょうか?

この質問に答えるには、x の回帰直線に 170 を挿入して y を解くだけです。

ŷ = 32.7830 + 0.2001(170) = 66.8 インチ

体重が 150 ポンドの人の場合、身長はどのくらいだと予想すべきでしょうか?

この質問に答えるには、x の回帰直線に 150 を挿入し、y を解くことができます。

ŷ = 32.7830 + 0.2001(150) = 62.798 インチ

注意:このような質問に答えるために回帰式を使用する場合は、データセット内の予測子変数の範囲内にある予測子変数の値のみを使用してください。最小二乗回帰直線を生成するために使用した原点。たとえば、データセット内の体重は 140 ～ 212 ポンドの範囲でした。したがって、体重が 140 ～ 212 ポンドの場合に予想される身長についての質問に答えるのは理にかなっています。

決定係数

最小二乗回帰直線がデータにどの程度「適合」するかを測定する 1 つの方法は、R ²で示される決定係数を使用することです。

決定係数は、予測変数によって説明できる応答変数の分散の割合です。

決定係数は 0 から 1 まで変化します。値 0 は、応答変数が予測変数によってまったく説明できないことを示します。値 1 は、応答変数が予測変数によって誤差なく完全に説明できることを示します。

0 と 1 の間のR ^{2 は}、応答変数が予測変数によってどの程度説明できるかを示します。たとえば、R ²が 0.2 の場合、応答変数の分散の 20% が予測変数によって説明できることを示します。 R ²が 0.77 の場合、応答変数の分散の 77% が予測変数によって説明できることを示します。

前回の結果では、R ²が 0.9311 という結果が得られたことに注意してください。これは、身長の変動の 93.11% が体重予測変数によって説明できることを示しています。

これは、体重が身長の非常に良い指標であることを示しています。

線形回帰の仮定

線形回帰モデルの結果が有効で信頼できるものであるためには、次の 4 つの前提が満たされていることを確認する必要があります。

1. 線形関係:独立変数 x と従属変数 y の間には線形関係があります。

2. 独立性:残差は独立しています。特に、時系列データ内の連続する残差間に相関はありません。

3. 等分散性:残差は x の各レベルで一定の分散を持ちます。

4. 正規性:モデルの残差は正規分布します。

これらの仮定の 1 つ以上が満たされない場合、線形回帰の結果は信頼性が低いか、誤解を招く可能性があります。

各前提の説明、前提が満たされているかどうかを判断する方法、前提が満たされていない場合の対処方法については、 この記事を参照してください。