Google スプレッドシートで線形回帰を実行する方法
線形回帰は、1 つ以上の説明変数と応答変数の間の関係を定量化するために使用できる方法です。
説明変数が 1 つだけの場合は単回帰を使用し、説明変数が 2 つ以上の場合は重回帰を使用します。
どちらのタイプの回帰も、次の構文を使用する Google スプレッドシートのLINEST()関数を使用して実行できます。
LINEST (known_data_y、known_data_x、calculate_b、verbose)
金：
- known_data_y:応答値の配列
- known_data_x:説明値のテーブル
- Calculate_b:切片を計算するかどうかを示します。これはデフォルトで TRUE であり、線形回帰ではそのままにしておきます。
- 詳細:傾きと切片を超える追加の回帰統計を提供するかどうかを示します。これはデフォルトでは FALSE ですが、例では TRUE であると指定します。
次の例は、この関数を実際に使用する方法を示しています。
Google スプレッドシートでの単純な線形回帰
勉強時間と試験結果の関係を理解したいとします。試験勉強と試験で得た成績。
この関係を調べるために、説明変数として学習時間を使用し、応答変数として試験のスコアを使用して単純な線形回帰を実行できます。
次のスクリーンショットは、セル D2 で次の数式が使用されている 20 人の生徒のデータ セットを使用して単純な線形回帰を実行する方法を示しています。
= LINE ( B2:B21 、 A2:A21 、 TRUE 、 TRUE )
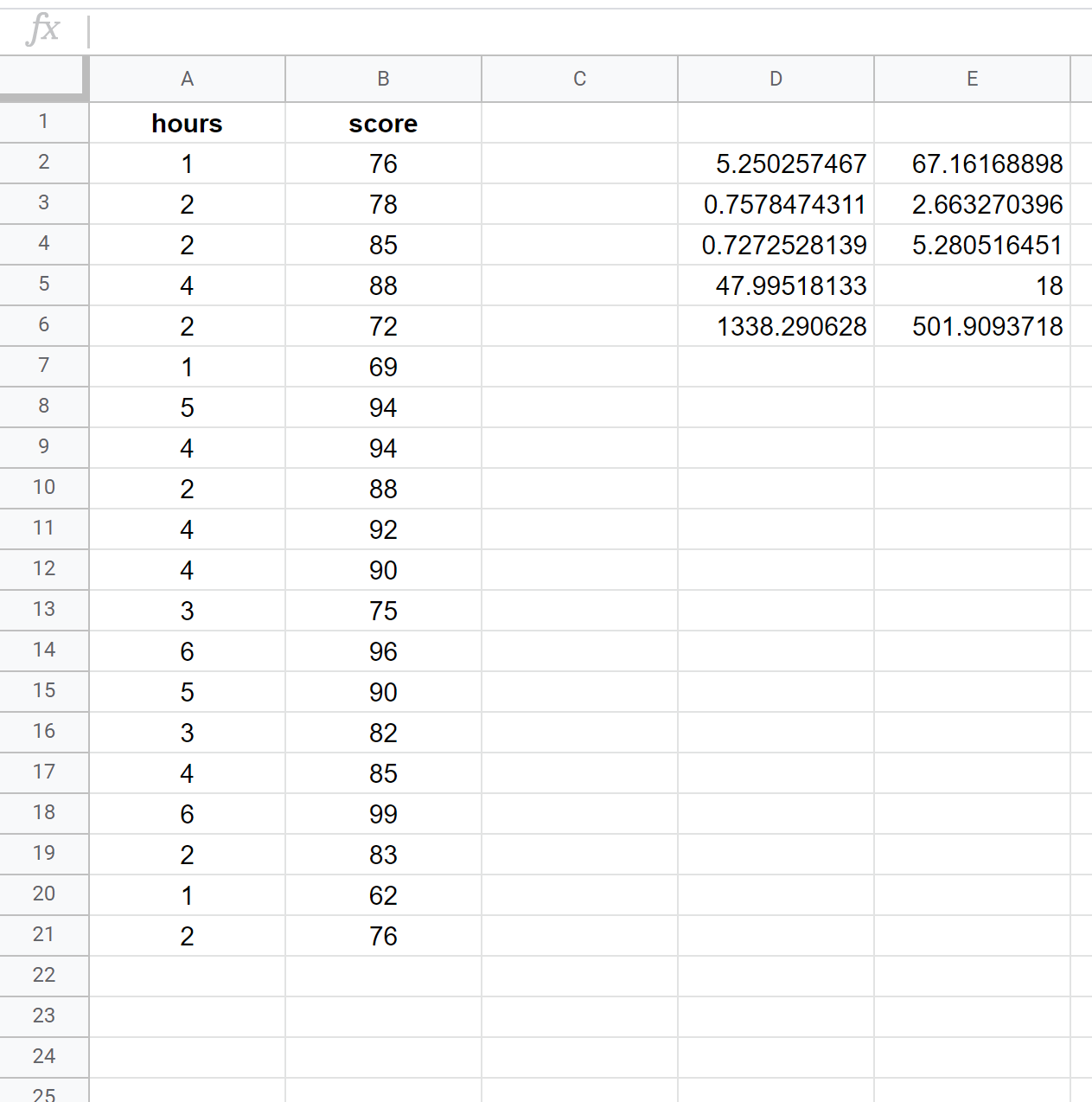
次のスクリーンショットは、出力の注釈を示しています。
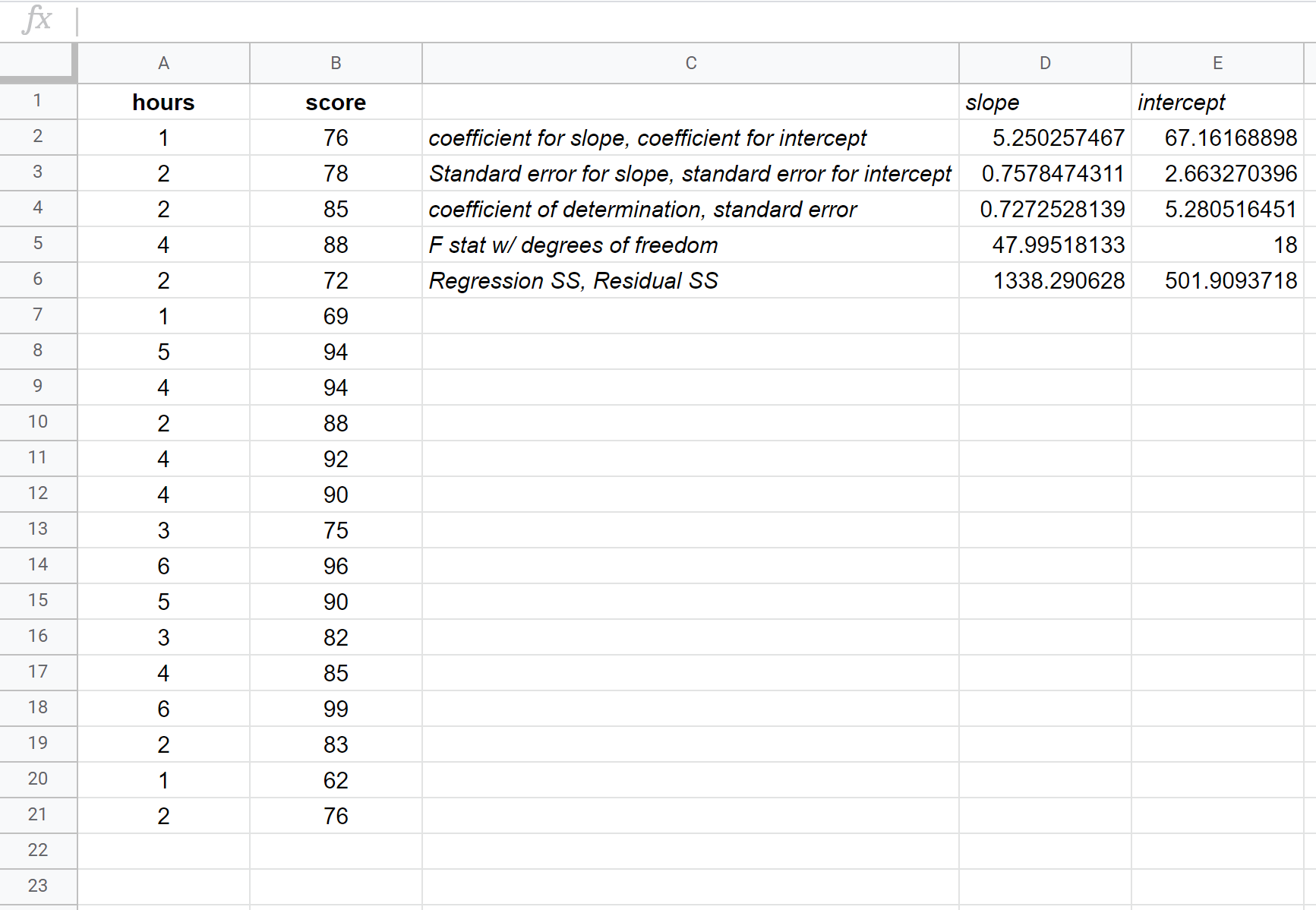
結果内の最も関連性の高い数値を解釈する方法は次のとおりです。
R 平方: 0.72725 。これを決定係数といいます。説明変数によって説明できる応答変数の分散の割合です。この例では、試験得点の変動の約 72.73% は勉強時間数によって説明できます。
標準誤差: 5.2805 。これは、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均して 5.2805 単位外れています。
係数:係数は、推定された回帰式を書くために必要な数値を与えます。この例では、推定される回帰式は次のようになります。
試験スコア = 67.16 + 5.2503*(時間)
時間係数は、学習時間が追加されるごとに、試験のスコアが平均5.2503増加することを意味すると解釈します。切片の係数は、勉強時間が 0 時間の学生の予想される試験スコアが67.16であることを意味すると解釈します。
この推定回帰式を使用して、学習時間数に基づいて生徒の予想される試験スコアを計算できます。たとえば、3 時間勉強した生徒は、試験スコア82.91を達成する必要があります。
試験のスコア = 67.16 + 5.2503*(3) = 82.91
Google スプレッドシートでの重線形回帰
勉強に費やした時間数と予備試験の受験数が、学生が特定の大学入学試験で取得する成績に影響するかどうかを知りたいとします。
この関係を調べるために、学習時間と受けた予備試験を説明変数として、試験結果を応答変数として使用して重線形回帰を実行できます。
次のスクリーンショットは、セル E2 で次の数式が使用されている 20 人の生徒のデータ セットを使用して重線形回帰を実行する方法を示しています。
=右( C2:C21 、 A2:B21 、 TRUE 、 TRUE )
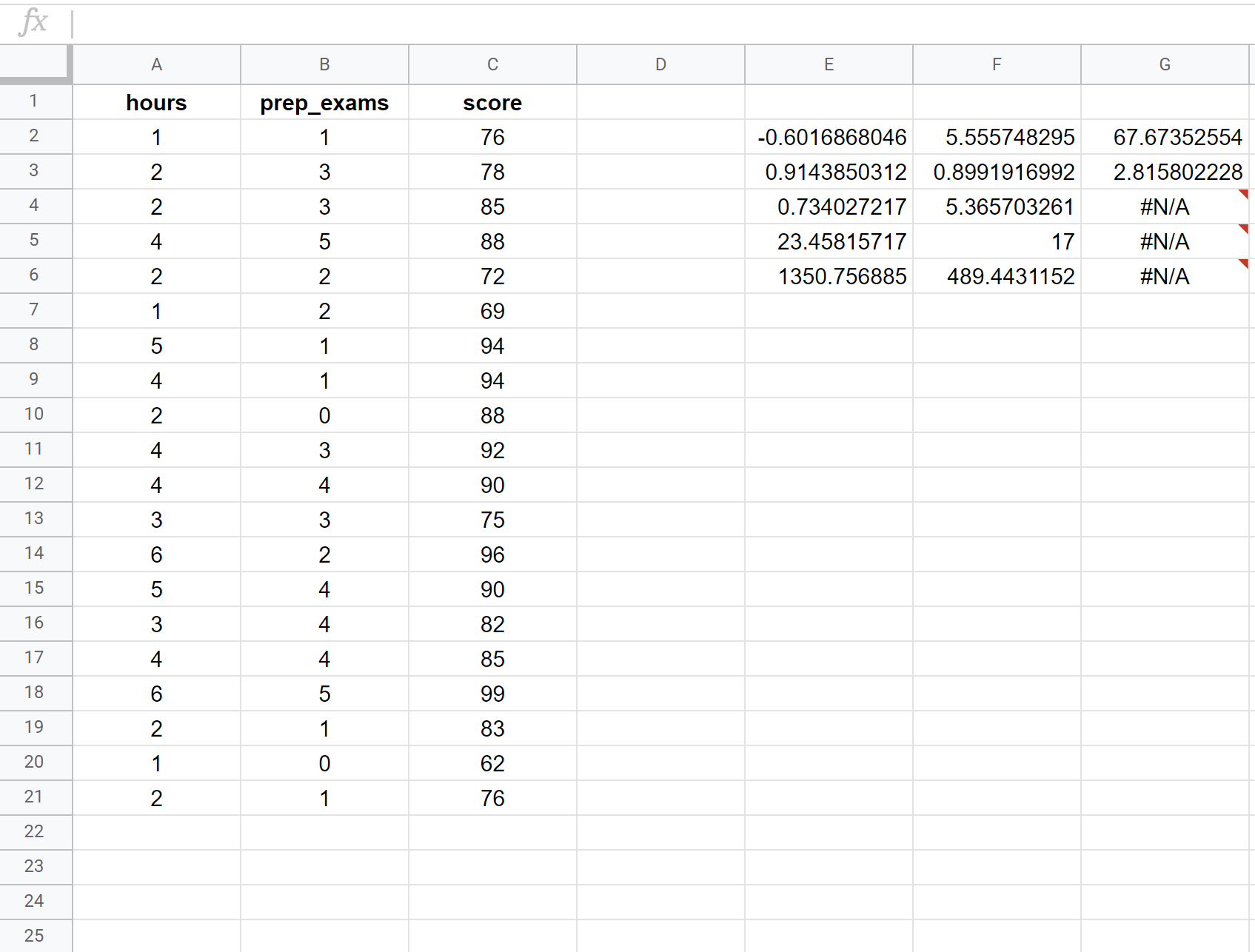
結果内の最も関連性の高い数値を解釈する方法は次のとおりです。
R スクエア: 0.734 。これを決定係数といいます。説明変数によって説明できる応答変数の分散の割合です。この例では、試験得点の変動の 73.4% は、勉強時間数と受験した予備試験の数によって説明されます。
標準誤差: 5.3657 。これは、観測値と回帰直線の間の平均距離です。この例では、観測値は回帰直線から平均して 5.3657 単位外れています。
推定回帰式:モデル出力の係数を使用して、次の推定回帰式を作成できます。
試験スコア = 67.67 + 5.56*(時間数) – 0.60*(予備試験)
この推定回帰式を使用して、学習時間数と受験した模擬試験の数に基づいて、生徒の予想される試験スコアを計算できます。たとえば、3 時間勉強して予備試験を受ける学生は、 83.75の成績を取得する必要があります。
試験のスコア = 67.67 + 5.56*(3) – 0.60*(1) = 83.75
追加リソース
次のチュートリアルでは、Google スプレッドシートで他の一般的なタスクを実行する方法を説明します。
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る