調整後のオッズ比: 定義と例
統計学では、オッズ比は、治療グループで発生する事象の確率と対照グループで発生する事象の確率の間の比率を示します。
オッズ比は、1 つ以上の予測子変数と 2 値応答変数を持つ回帰モデルを近似するために使用する手法であるロジスティック回帰で最も一般的に現れます。
調整済みオッズ比は、モデル内の他の予測子変数に対して調整されたオッズ比です。
これは、他の予測変数の影響を調整した後、予測変数がイベント発生の確率にどのような影響を与えるかを理解するのに特に役立ちます。
次の例は、オッズ比と調整されたオッズ比の違いを示しています。
例: 調整後のオッズ比の計算
母親の年齢が低出生体重児の赤ちゃんが生まれる確率に影響を与えるかどうかを知りたいとします。
これを調べるために、年齢を予測変数として、低出生体重 (はいまたはいいえ) を応答変数として使用してロジスティック回帰を実行できます。
300 人の母親に関するデータを収集し、ロジスティック回帰モデルを当てはめるとします。結果は次のとおりです。
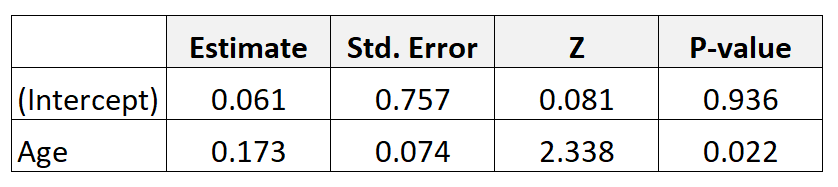
年齢のオッズ比を取得するには、表からの係数推定値を単純に累乗します: e 0.173 = 1.189 。
これは、年齢が 1 歳上がると、赤ちゃんが低出生体重児になる確率が1,189増加することを示しています。言い換えれば、低出生体重児の赤ちゃんが生まれる確率は、年齢が毎年増加するごとに18.9%増加します。
このオッズ比は、モデル内の唯一の予測子変数であるため、モデル内の他の予測子変数に対して調整されていないため、「粗」オッズ比または「未調整」オッズ比と呼ばれます。
しかし、母親の年齢と喫煙習慣が低出生体重児の赤ちゃんが生まれる確率に影響を与えるかどうかを理解したいとします。
これを調べるために、年齢と喫煙 (はいまたはいいえ) を予測変数として、低出生体重を応答変数として使用してロジスティック回帰を実行できます。
300 人の母親に関するデータを収集し、ロジスティック回帰モデルを当てはめるとします。結果は次のとおりです。
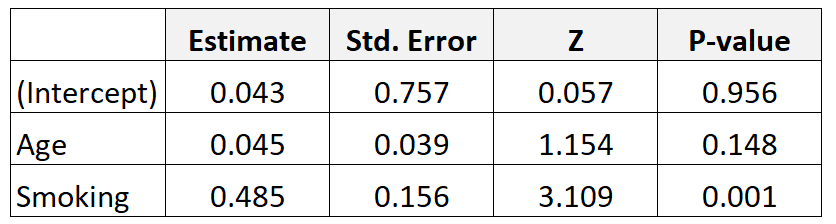
結果を解釈する方法は次のとおりです。
年齢:年齢調整されたオッズ比は次のように計算されます: e 0.045 = 1.046 。これは、喫煙変数が一定であると仮定すると、低出生体重児の赤ちゃんが生まれる確率は、年齢が毎年増加するごとに 4.6% 増加することを意味します。
たとえば、母親 A と母親 B が両方とも喫煙しているとします。母親 A が母親 B より 1 歳年上である場合、母親 A が低出生体重児を産む確率は、母親 B が低出生体重児を産む確率の 1.046 倍です。
喫煙: 喫煙に関する調整後のオッズ比は次のように計算されます: e.485 = 1.624 。これは、年齢変数が一定であると仮定すると、母親が喫煙すると、低出生体重児が生まれる確率が(非喫煙と比較して)62.4%増加することを意味します。
たとえば、母親Aと母親Bはどちらも30歳だとします。母親 A が妊娠中に喫煙し、母親 B が喫煙しない場合、母親 A が低出生体重児を生む確率は、母親 B が低出生体重児を生む確率より 62.4% 高くなります。
年齢調整後のオッズ比は、前の例の未調整のオッズ比よりも低いことに注意してください。これは、他の予測変数が応答変数が発生する可能性を高めると、モデルにすでに存在する予測変数の調整されたオッズ比が常に減少するためです。
概要: オッズ比と調整後のオッズ比
オッズ比(「粗い」オッズ比とも呼ばれます) は、予測変数の変化が応答変数が発生する確率にどのような影響を与えるかを知るのに役立ちます。
調整されたオッズ比は、モデル内の他の予測変数を制御した後、予測変数の変化が応答変数が発生する確率にどのような影響を与えるかを知るのに役立ちます。
追加リソース
ロジスティック回帰の概要
R でロジスティック回帰を実行する方法
Python でロジスティック回帰を実行する方法