負の二項対ポアソン: 回帰モデルの選択方法
負の二項回帰とポアソン回帰は、応答変数が離散カウント結果で表される場合に使用する必要がある 2 種類の回帰モデルです。
以下に、離散計数結果を表す応答変数の例をいくつか示します。
- 特定のプログラムを卒業した学生の数
- ある交差点での交通事故件数
- マラソン完走者数
- 小売店における特定の月の返品数
分散が平均にほぼ等しい場合、ポアソン回帰モデルは一般にデータセットによく適合します。
ただし、分散が平均よりも大幅に大きい場合は、通常、負の二項回帰モデルの方がデータをよりよく適合させることができます。
特定のデータセットに対してポアソン回帰と負の二項回帰のどちらが適切であるかを判断するために使用できる手法が 2 つあります。
1. 残りのプロット
回帰モデルからの予測値に対する標準化残差のプロットを作成できます。
標準化残差の大部分が -2 ~ 2 の範囲にある場合は、ポアソン回帰モデルが適切である可能性があります。
ただし、多くの残差がこの範囲外にある場合は、負の二項回帰モデルの方がより適切に適合する可能性があります。
2. 尤度比検定
ポアソン回帰モデルと負の二項回帰モデルを同じデータセットに当てはめて、尤度比検定を実行できます。
検定の p 値が特定の有意水準 (0.05 など) を下回っている場合、負の二項回帰モデルの方が大幅に良好な適合を提供すると結論付けることができます。
次の例は、R でこれら 2 つの手法を使用して、特定のデータ セットに対してポアソン回帰モデルと負の二項回帰モデルのどちらを使用する方が良いかを判断する方法を示しています。
例: 負の二項回帰とポアソン回帰
特定の郡の高校野球選手が学校区分 (「A」、「B」、または「C」) と学年に基づいて受け取った奨学金の数を知りたいとします。大学入学試験(0から100で評価)。 )。
次の手順を使用して、負の二項回帰モデルとポアソン回帰モデルのどちらがデータによりよく適合するかを判断します。
ステップ 1: データを作成する
次のコードは、1,000 人の野球選手に関するデータを含むデータセットを作成します。
#make this example reproducible set. seeds (1) #create dataset data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100), rep(3, 70), rep(4, 30)), division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ), exam = c(runif(700, 60, 90), runif(100, 65, 95), runif(200, 75, 95))) #view first six rows of dataset head(data) offers division exam 1 0 A 66.22635 2 0 C 66.85974 3 0 A 77.87136 4 0 B 77.24617 5 0 A 62.31193 6 0 C 61.06622
ステップ 2: ポアソン回帰モデルと負の二項回帰モデルを当てはめる
次のコードは、ポアソン回帰モデルと負の二項回帰モデルの両方をデータに適合させる方法を示しています。
#fit Poisson regression model p_model <- glm(offers ~ division + exam, family = ' fish ', data = data) #fit negative binomial regression model library (MASS) nb_model <- glm. nb (offers ~ division + exam, data = data)
ステップ 3: 残差プロットを作成する
次のコードは、両方のモデルの残差プロットを作成する方法を示しています。
#Residual plot for Poisson regression p_res <- resid (p_model) plot(fitted(p_model), p_res, col=' steelblue ', pch=16, xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ') abline(0,0) #Residual plot for negative binomial regression nb_res <- resid (nb_model) plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16, xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ') abline(0,0)
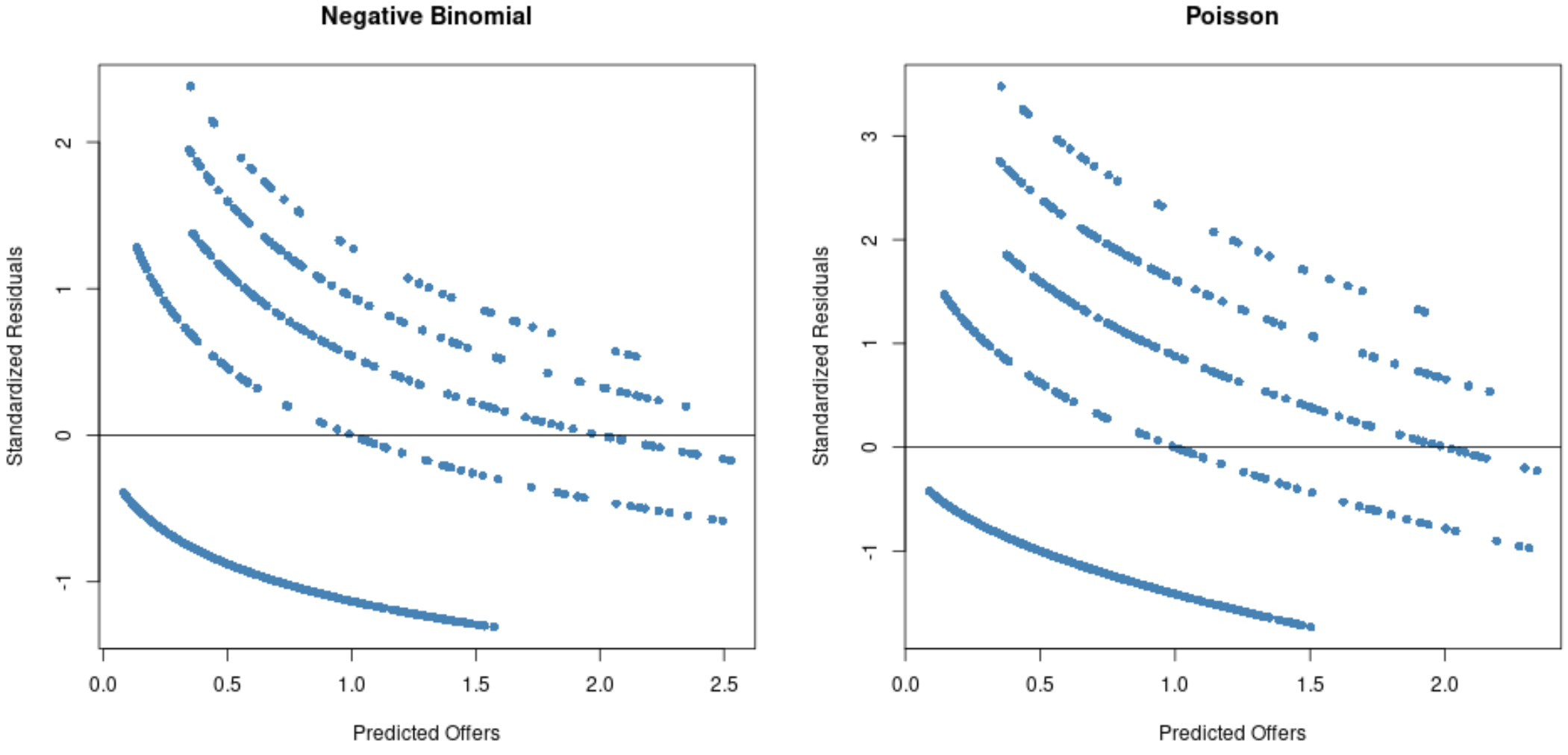
グラフから、負の二項回帰モデルと比較して、ポアソン回帰モデルでは残差がさらに広がっていることがわかります (一部の残差は 3 を超えて広がることに注意してください)。
これは、負の二項回帰モデルの方が残差が小さいため、おそらくこのモデルの方が適切であることを示しています。
ステップ 4: 尤度比検定を実行する
最後に、尤度比検定を実行して、2 つの回帰モデルの適合に統計的に有意な差があるかどうかを判断できます。
pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE ) 'log Lik.' 3.508072e-29 (df=5)
検定の p 値は3.508072e-29であることがわかり、これは 0.05 よりも大幅に小さくなります。
したがって、負の二項回帰モデルは、ポアソン回帰モデルと比較してデータへの適合性が大幅に優れていると結論付けることができます。