超幾何分布

によるベンジャミン・アンダーソン博士 8月 6, 2023 確率 0コメント

この記事では、超幾何分布とは何か、およびこのタイプの分布で確率がどのように計算されるかについて説明します。超幾何分布の公式、その特性、および超幾何分布の確率を計算する計算機がオンラインで見つかります。

超幾何分布とは何ですか?

超幾何分布は、母集団からn 個の要素を置換せずにランダムに抽出した場合に成功したケースの数を表す確率分布です。

つまり、超幾何分布は、いずれも置換せずに母集団からn個の要素を抽出するときにx 個の成功が得られる確率を計算するために使用されます。

超幾何分布には 3 つのパラメータがあります。

N : は母集団内の要素の数です (N = 0、1、2、…)。
K : 成功ケースの最大数です (K = 0、1、2、…、N)。超幾何分布では要素は「成功」または「失敗」としか考えられないため、 NKは失敗ケースの最大数です。
n : は、実行される非置換フェッチの数です。

$X \sim HG(N,K,n)$

たとえば、パラメータ N=8、K=5、n=3 の超幾何分布を持つ離散確率変数 X は次のように定義されます。

$X \sim HG(8,5,3)$

超幾何分布式

超幾何分布の公式は、 x上のKの組み合わせ数とnx上のNKの組み合わせ数をn上のNの組み合わせ数で割った積です。

ここで、 Nは母集団サイズ、 Kは有利なケースの総数、 nは非置換抽出の数、 xは発生確率を計算する必要がある有利なケースの数です。

👉以下の計算機を使用して、超幾何分布に従う変数のイベントの確率を計算できます。

超幾何分布の例

超幾何分布の定義と公式を理解したら、次は超幾何分布の確率の計算方法を理解できるように、例を段階的に解決していきます。

袋の中に青いボール20個と赤いボール30個を入れます。つまり、袋の中には合計50個のボールがあります。何も交換せずに 12 個のボールを引いた場合、青いボールを 4 個引く確率を求めます。

この演習を解くために最初に行う必要があるのは、超幾何分布のパラメーターを特定することです。この場合、母集団の要素の総数は 50 ( N = 50) で、有利なケースの最大数は 20 ( K = 20) で、12 個のボールが描画されます ( n = 12)。

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

4 つの青いボール ( x =4) を引く確率を計算したいので、超幾何分布式を適用し、変数を対応する値に置き換えて計算を実行します。

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

超幾何分布計算機

次のオンライン計算ツールに超幾何分布のパラメーターを入力して、目的のイベントの発生確率を計算します。

Nは母集団のサイズ、 Kは有利なケースの総数、 nはサンプルサイズ、 xはこれが起こる確率を求める値であることに注意してください。

超幾何分布の特徴

超幾何分布には次の特性があります。

超幾何分布の期待値は、サンプル内の要素の数に有利なケースの総数を乗算し、母集団内の要素の数で割った値に等しくなります。

$E[X]=\cfrac{n\cdot K}{N}$

超幾何分布の最頻値は、 n+1とK+1の積をN+2で割った値から切り捨てられた値です。

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

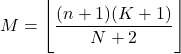
超幾何分布の分散は、次の式を使用して取得できます。

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

超幾何分布のモーメント母関数は次のとおりです。

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

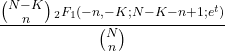
超幾何分布の特性関数は次のとおりです。

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

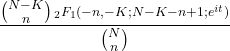
指定された数のイベントが発生する確率は、超幾何分布の再帰関数を使用して、前の数値の確率から計算できます。

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

超幾何分布と二項分布

超幾何分布と二項分布の違いは置換です。超幾何分布は検索が置換されない場合に使用されますが、二項分布では検索が置換されます。

たとえば、デッキ内で 5 枚のカードをランダムに引き、特定のカードが得られる確率を計算したい場合、引いた各カードを置き換えない場合、計算を行うために超幾何分布を使用する必要があります。ただし、カードを削除するときに次の抽出を実行する前にカードを元に戻す場合は、二項分布を使用して確率を計算する必要があります。

数Nが大きく、比n/Nが小さく、望ましい有利なケースの数が非常に少ない場合、二項分布の近似として超幾何分布を使用できます。ただし、結果の信頼性が低く、さらに、超幾何法則よりも二項法則を使用した方が確率を計算するのが簡単であるため、これはお勧めしません。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る