逆正規分布: 定義と例
逆正規分布という用語は、既知の確率を使用して正規分布内の対応する Z 臨界値を見つける方法を指します。
これを、連続確率分布である逆ガウス分布と混同しないでください。
このチュートリアルでは、さまざまな統計ソフトウェアで逆正規分布を使用する例をいくつか示します。
逆正規分布には TI-83 または TI-84 計算機があります
「逆正規分布」という用語は、TI-83 または TI-84 計算機で最も頻繁に使用されます。この計算機では、次の関数を使用して、特定の確率に対応する臨界 Z 値を見つけます。
invNorm(確率, μ, σ)
金:
- 確率:有意性のレベル
- μ:母集団平均
- σ:母集団標準偏差
TI-84 電卓でこの関数にアクセスするには、 2nd を押してからvarsを押します。これにより、 DISTR画面が表示され、そこでinvNorm()を使用できます。

たとえば、この関数を使用して、確率値 0.05 に対応する Z 臨界値を見つけることができます。
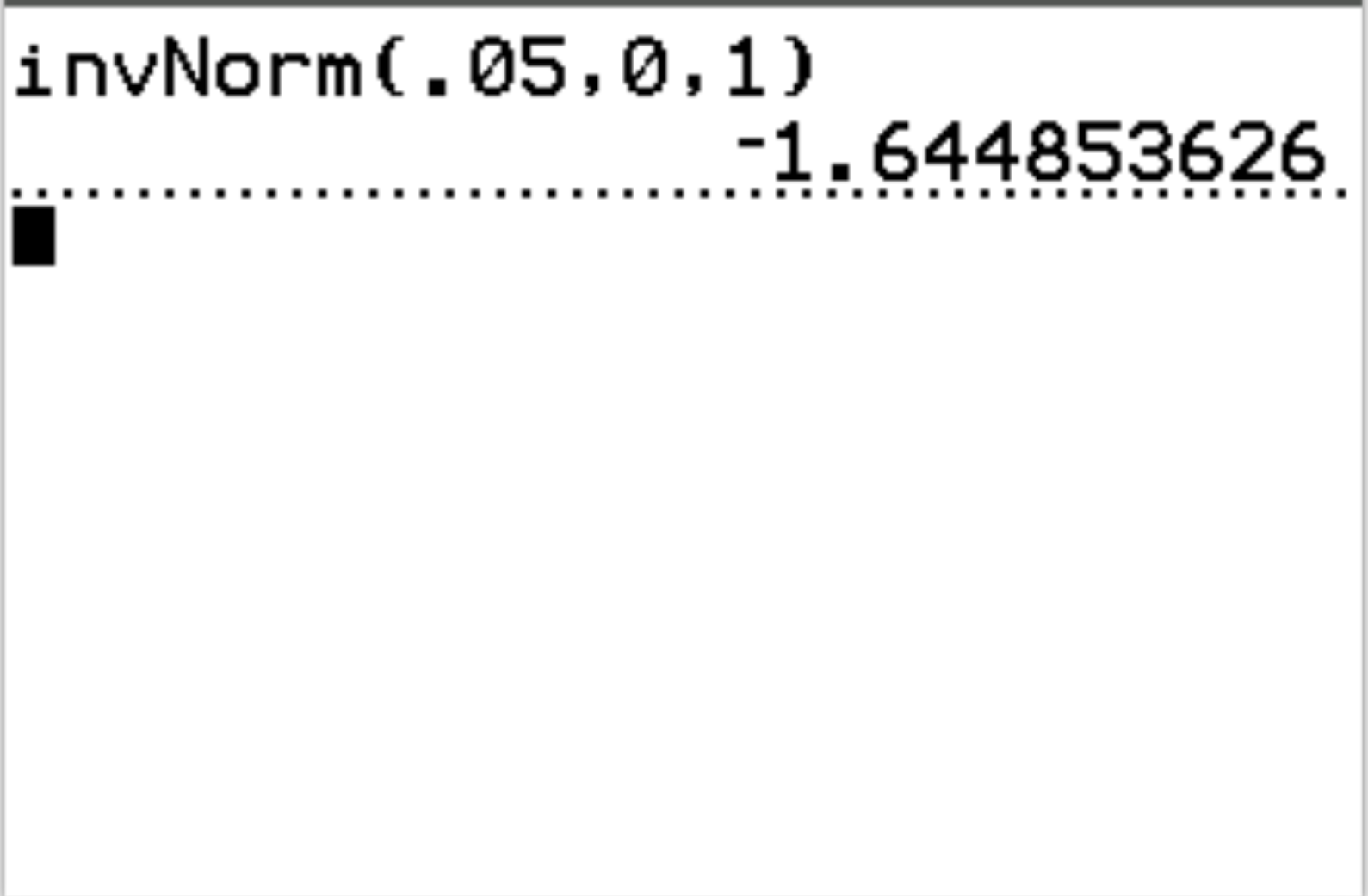
確率値 0.05 に対応する臨界 z 値は-1.64485です。
関連: TI-84 電卓で invNorm を使用する方法 (例付き)
Excelの逆正規分布
Excel で特定の確率値に関連付けられた Z クリティカル値を見つけるには、次の構文を使用するINVNORM()関数を使用できます。
INVNORM(p, 平均, sd)
金:
- p:重要度
- 平均:母集団の平均
- sd:母集団標準偏差
たとえば、この関数を使用して、確率値 0.05 に対応する Z 臨界値を見つけることができます。
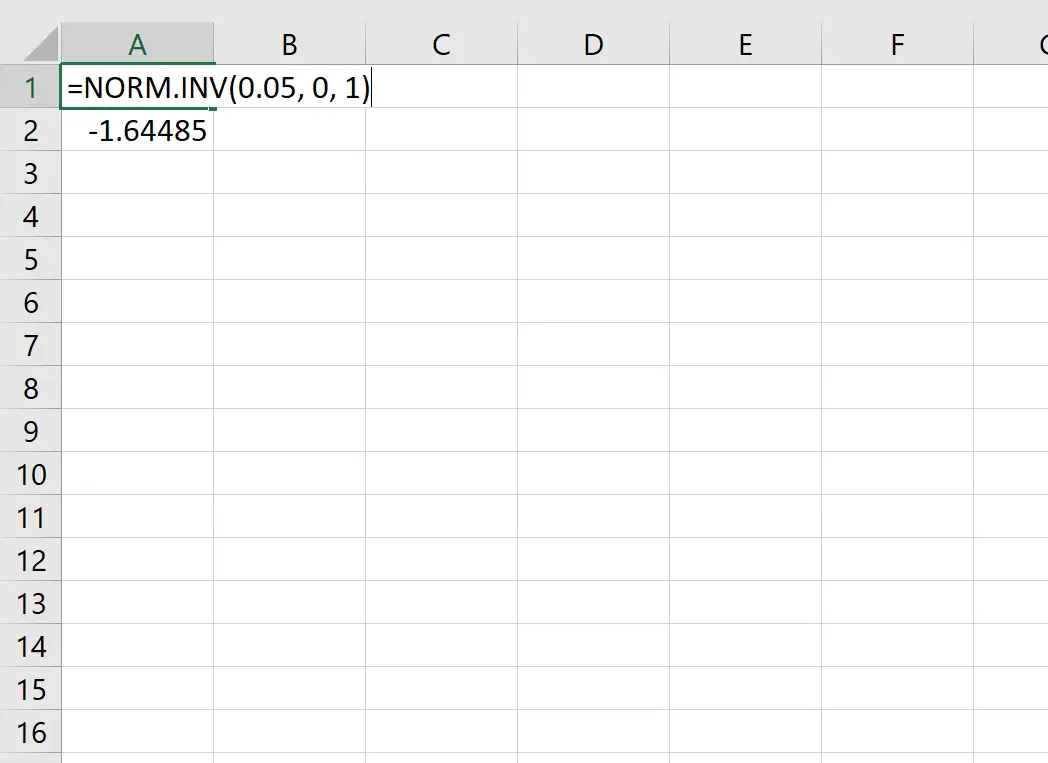
確率値 0.05 に対応する臨界 z 値は-1.64485です。
R の逆正規分布
R の特定の確率値に関連付けられた Z 臨界値を見つけるには、次の構文を使用するqnorm()関数を使用できます。
qnorm (p、平均、sd)
金:
- p:重要度
- 平均:母集団の平均
- sd:母集団標準偏差
たとえば、この関数を使用して、確率値 0.05 に対応する Z 臨界値を見つけることができます。
qnorm (p= .05 , mean= 0 , sd= 1 ) [1] -1.644854
繰り返しになりますが、確率値 0.05 に対応する臨界 Z 値は-1.64485です。