限界分布とは何ですか?
双方向度数表は、 2 つのカテゴリ変数の頻度 (または「カウント」) を表示する表です。
たとえば、次の二元表は、100 人に野球、バスケットボール、サッカーのどのスポーツが好きかを尋ねたアンケートの結果を示しています。
行には回答者の性別が表示され、列には回答者が選択したスポーツが表示されます。

この例には、スポーツとジェンダーという 2 つの変数があります。
周辺分布は、単にこれらの個々の変数の分布です。二元配置表では、周辺分布が表の余白に表示されます。
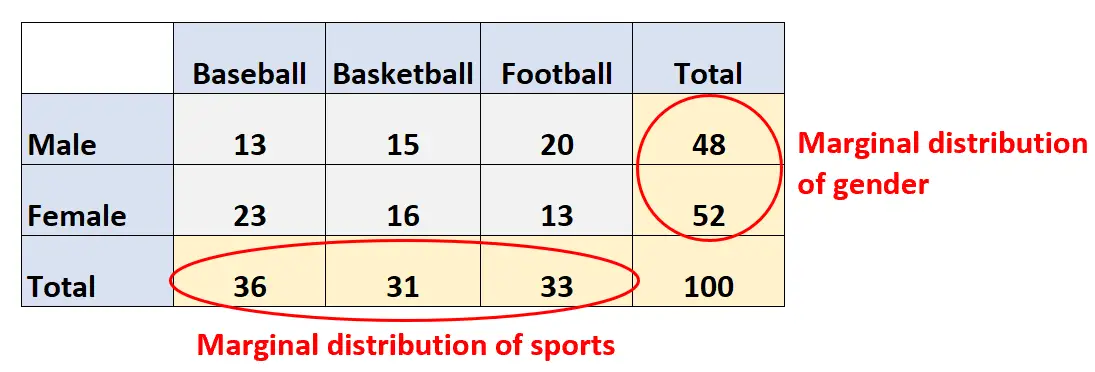
たとえば、スポーツの限界分布は次のようになります。
- 野球: 36
- バスケットボール: 31
- サッカー: 33
スポーツの限界分布をパーセンテージとして書くこともできます (つまり、合計 100 人の回答者に対する)。
- 野球: 36/100 = 36%
- バスケットボール: 31/100 = 31%
- サッカー: 33/100 = 33%
そして、限界性別分布は次のようになります。
- 男性: 48 (または 48%)
- 女性: 52 (または 52%)
注:限界分布は常に合計して 100% になります。
なぜ限界分布を使用するのでしょうか?
周辺分布は、2 つの変数 (スポーツと性別など) のデータを収集することがよくありますが、1 つの変数についてのみ特定の質問がある場合があるため便利です。
たとえば、性別のみに基づいて調査回答者の分布を知りたい場合があります。
この場合、周辺分布を使用すると、回答者の 48% が男性で、回答者の 52% が女性であることがわかります。
限界分布をより深く理解するための練習として、次の例を使用してください。
例 1: パーセンテージの限界分布
次の二元表は、238 人にどのような種類の映画が好きかを尋ねたアンケートの結果を示しています。
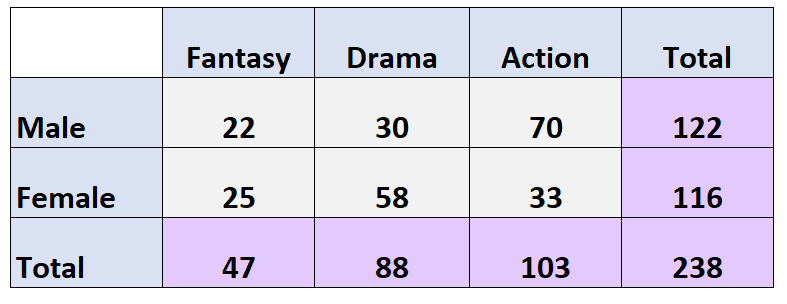
質問:映画ジャンル別の限界分布はどのくらいですか (パーセント)?
回答:映画ジャンルの限界分布は次のとおりです。
- ファンタジー: 47/238 = 19.7%
- ドラマ: 88/238 = 37%
- アクション: 103/238 = 43.3%
質問:限界性別分布 (パーセンテージ) はどれくらいですか?
回答:性別による限界分布は次のとおりです。
- 男性: 122/238 = 51.3%
- 女性: 116/238 = 48.7%
例 2: 口座の限界分配
次の二元表は、クラスの 64 人の生徒の試験の得点を、勉強に費やした時間数に基づいて示しています。
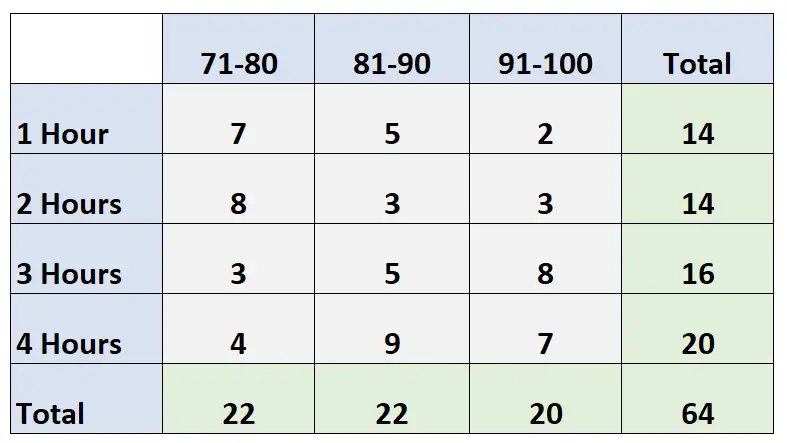
質問:試験得点の限界分布 (数値) はどれくらいですか?
回答:試験得点の限界分布は次のとおりです。
- 71-80: 22
- 81-90: 22
- 91-100: 20
質問:学習時間(数)の限界分布はどれくらいですか?
回答:学習時間の限界分布は次のとおりです。
- 1時間: 14
- 2時間: 14
- 3時間: 16
- 4時間: 20分
周辺分布の合計は、64 人の生徒のテーブルの合計と一致することに注意してください。
追加リソース
記述統計または推論統計
質的変数と量的変数
測定レベル: 名目、順序、間隔、比率