離散一様分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 確率 0コメント

この記事では、離散一様分布とは何か、その特徴的な公式は何かについて説明します。同様に、離散一様分布のグラフ表現とその特性を確認することができます。

離散一様分布とは何ですか?

離散一様分布は、すべての値が等確率である離散確率分布です。つまり、離散一様分布では、すべての値が同じ発生確率を持ちます。

たとえば、考えられるすべての結果 (1、2、3、4、5、または 6) の発生確率が同じであるため、サイコロの目は離散一様分布で定義できます。

一般に、離散一様分布には、分布が取り得る値の範囲を定義する 2 つの特性パラメータaとbがあります。したがって、変数が離散一様分布で定義されている場合は、 Uniform(a,b)と書かれます。

すべての結果が同じ確率を持つ場合、実験がランダムであることを意味するため、離散一様分布を使用してランダム実験を説明できます。

離散一様分布の式

離散一様分布の定義がわかったので、このタイプの分布の値の出現確率を計算できる式が何であるかを見てみましょう。

離散一様分布の確率関数は一定であり、その値は考えられる結果の総数の 1 に等しくなります。したがって、離散一様分布の式は次のようになります。

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

一方、離散一様分布の累積確率関数の式は次のとおりです。

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

金

$a$

そして

$b$

は離散一様分布の特性パラメータです。

離散一様分布図

離散一様分布は区間内で特定の値のみを取ることができるため、そのグラフ表現は点で構成されます。さらに、すべての確率は等しいため、離散一様分布内のすべての点は同じ垂直座標を持ちます。

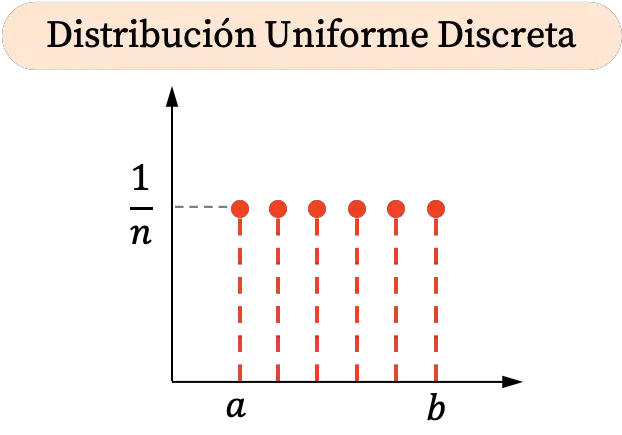
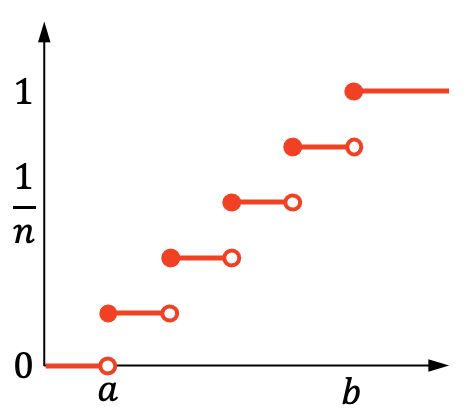
一方、離散一様分布の累積確率グラフは次のようになります。

離散一様分布の特徴

離散一様分布には次の特徴があります。

離散一様分布は、分布の可能な値の範囲を決定する 2 つの整数パラメーターaとbによって定義されます。

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

離散一様分布の平均は、その 2 つの特性パラメーターの合計を 2 で割ったものに等しくなります。

$E[X]=\cfrac{a+b}{2}$

離散一様分布の中央値は平均値と等しいため、同じ式で計算されます。

$Me=\cfrac{a+b}{2}$

離散一様分布の分散は、結果の総数の二乗から 1 を引いた値を 12 で割った値に等しくなります。

$Var(X)=\cfrac{n^2-1}{12}$

離散一様分布は平均に関して対称であるため、この確率分布の歪度係数はゼロです。

$A=0$

離散一様分布の尖度は、次の式を使用して計算できます。

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

離散一様分布と連続一様分布

最後に、離散一様分布と連続一様分布の違いを見ていきます。これらは 2 つの似たタイプの確率分布ですが、大きな違いがあるからです。

離散一様分布と連続一様分布の違いは、取り得る値にあります。離散一様分布は区間内で特定の値のみを取ることができますが、連続一様分布は定義された区間内で任意の値を取ることができます。

一般に、離散一様分布は整数値のみを取ることができますが、連続一様分布は小数値も取ることができます。

➤参照:連続一様分布

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る