非対称性の種類

によるベンジャミン・アンダーソン博士 8月 5, 2023 統計 0コメント

この記事では、統計にどれだけの種類の非対称性が存在するかを学びます。このように、各タイプの非対称性を例を挙げて説明し、さらに分布の非対称性がどのように計算されるかを理解できるようになります。

非対称にはどのような種類がありますか?

統計学では、次の 3種類の非対称性があります。

それぞれのタイプの非対称については、以下で詳しく説明します。

分布に正のスキューがある場合、グラフの右の裾が左の裾よりも長いことを意味します。つまり、分布には平均の右側により多くの異なる値があります。

前の例の曲線は、平均の左側よりも右側の値の方がはるかに多いため、明確に非対称です。グラフからわかるように、緑色で示されたバーはオレンジ色のバーよりもはるかに大きいです。

統計学では、グラフの左の裾が右の裾よりも長い場合、分布の歪みは負であると言われます。つまり、負に歪んだ分布とは、平均値の左側により多くの異なる値があることを意味します。

前のグラフを見ると、平均値の右側よりも左側の値が多くなっているため、曲線は負に歪んでいます。

平均の左側の値の数が平均の右側の値の数と等しい場合、分布は対称です。したがって、平均は対称軸として機能します。

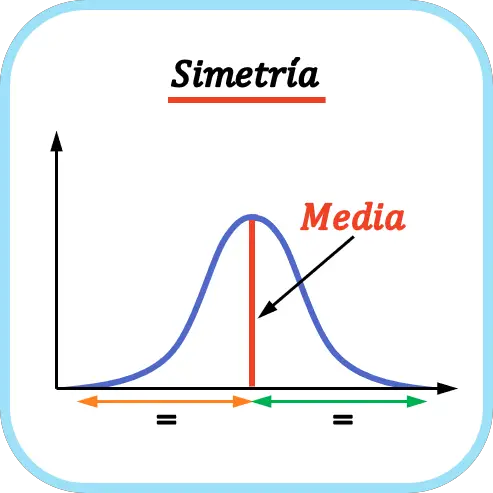
上の例に示されているように、表現された確率分布の平均値の左側の値の数は、平均値の右側の値の数と一致するため、対称的な分布になります。

統計におけるさまざまなタイプの非対称性が何であるかがわかったので、確率分布がどのタイプの非対称性に対応するかを知る方法を見てみましょう。

従来、分布の歪度の種類は、平均と中央値の関係 (大きいか、同等か、小さいか) に基づいて知ることができると説明されてきました。ただし、この特性は常に満たされるわけではありません。したがって、分布の歪度を決定するには、フィッシャーの歪度係数を計算する必要があります。

フィッシャーの非対称係数は、次の式を使用して計算されます。

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

または同等のもの:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

金

$E$

$\mu$

$\sigma$

フィッシャー係数が計算されると、その符号によって分布がどのような種類の非対称性を示すかを判断できるようになります。

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る