タイピング
この記事では、統計における分布の特徴付けが何を意味するのかについて説明します。したがって、類型化の定義、変数の類型化の例が見つかり、さらに、段階的に解決される演習で練習することができます。
タイピングとは何ですか?
統計学における正規化とは、分布の平均と標準偏差がそれぞれ 0 と 1 になるように線形変換を分布に適用するプロセスです。
より正確には、型付けには、確率変数から平均を減算し、それを標準偏差で割ることが含まれます。
タイピングは正規化または標準化とも呼ばれます。
入力式
変数を分類するには、その平均を減算し、それを標準偏差で割る必要があります。したがって、変数を入力するための式は次のようになります。
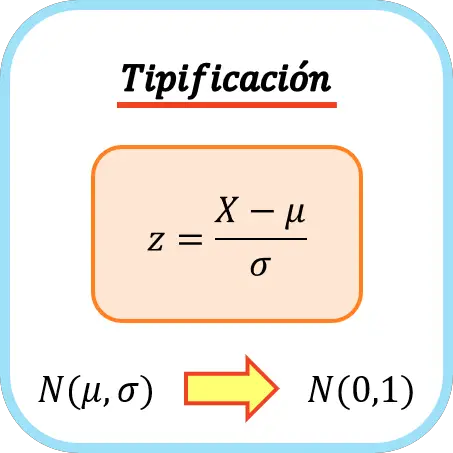
金
![]()
変数の平均です
![]()
そして
![]()
その標準偏差 (または標準偏差)。
したがって、線形変換が変数に適用されるため、エントリは実際には変数の変更になります。
入力例
類型化の定義とその公式を考慮して、概念を完全に理解するために、以下に具体的な例を示します。
- 連続確率変数は、平均 45、標準偏差 10 の正規分布に従います。60 以下の値が得られる確率はどれくらいですか?
![]()
正規分布の確率を見つけるには、その特性テーブルを使用する必要がありますが、これを行うには、まず型付けプロセスを実行する必要があります。したがって、平均を減算し、標準偏差で割って確率値を求めます。
![]()
標準化したら、正規分布確率テーブルに進み、値 1.5 がどの確率に対応するかを確認します。

正規分布の類型化テーブルからわかるように、前のステップで計算された値は次の確率に対応します。
![]()
したがって、60 以下の値が得られる確率は 93.32% になります。
タイピング練習が解決されました
平均と標準偏差がそれぞれ 120 と 50 である正規分布の次の確率を計算します。
![]()
- 208 以下の値が得られる確率。
- 137 より大きい値が得られる確率。
問題の両方のセクションで、確率を計算するために正規分布を入力する必要があります。
まず、208 以下の値の確率型を計算します。
![]()
次に、上の表で値 1.76 がどの確率に対応するかを見てみましょう。
![]()
次に、137 より大きい値を取得する確率を計算します。同様に、変数を入力することから始めます。
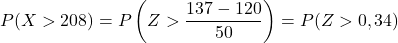 ただし、添付の表には最低の累積確率しか含まれていないため、この表を使用するには、まず確率を変換する必要があります。
ただし、添付の表には最低の累積確率しか含まれていないため、この表を使用するには、まず確率を変換する必要があります。
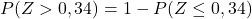 そして最後に、添付の表から、Z の計算値に対応する確率に注目します。
そして最後に、添付の表から、Z の計算値に対応する確率に注目します。
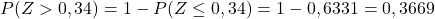
タイピングの意味は何ですか?
類型化の意味を理解するには、それが何に使用されるのか、変数をいつ型付けする必要があるのかを見ていきます。
主に、標準化は、異なる平均と分散を持つ分布の値を比較するために使用されます。同様に、標準化は確率の計算にも使用されます。
特性の異なる 2 つの分布の値を標準化することで、分布全体に対してどちらの値が大きいか小さいかを確認できます。言い換えれば、類型化プロセスを適用することで、どの値が分布の平均に最も近いか最も遠いかを確認できます。
さらに、上で説明したように、一般に確率テーブルは類型化された分布に基づいているため、類型化によって確率の計算も可能になります。