食品検査とは何ですか? (説明と例)
チャウ検定は、経済学者グレゴリー・チョウによって開発された統計検定で、異なるデータセットに対する 2 つの異なる回帰モデルの係数が等しいかどうかを検定するために使用されます。
チャウ テストは通常、時系列データを使用した計量経済学の分野で、特定の時点でデータに構造的な断絶があるかどうかを判断するために使用されます。
たとえば、次の散布図を考えてみましょう。
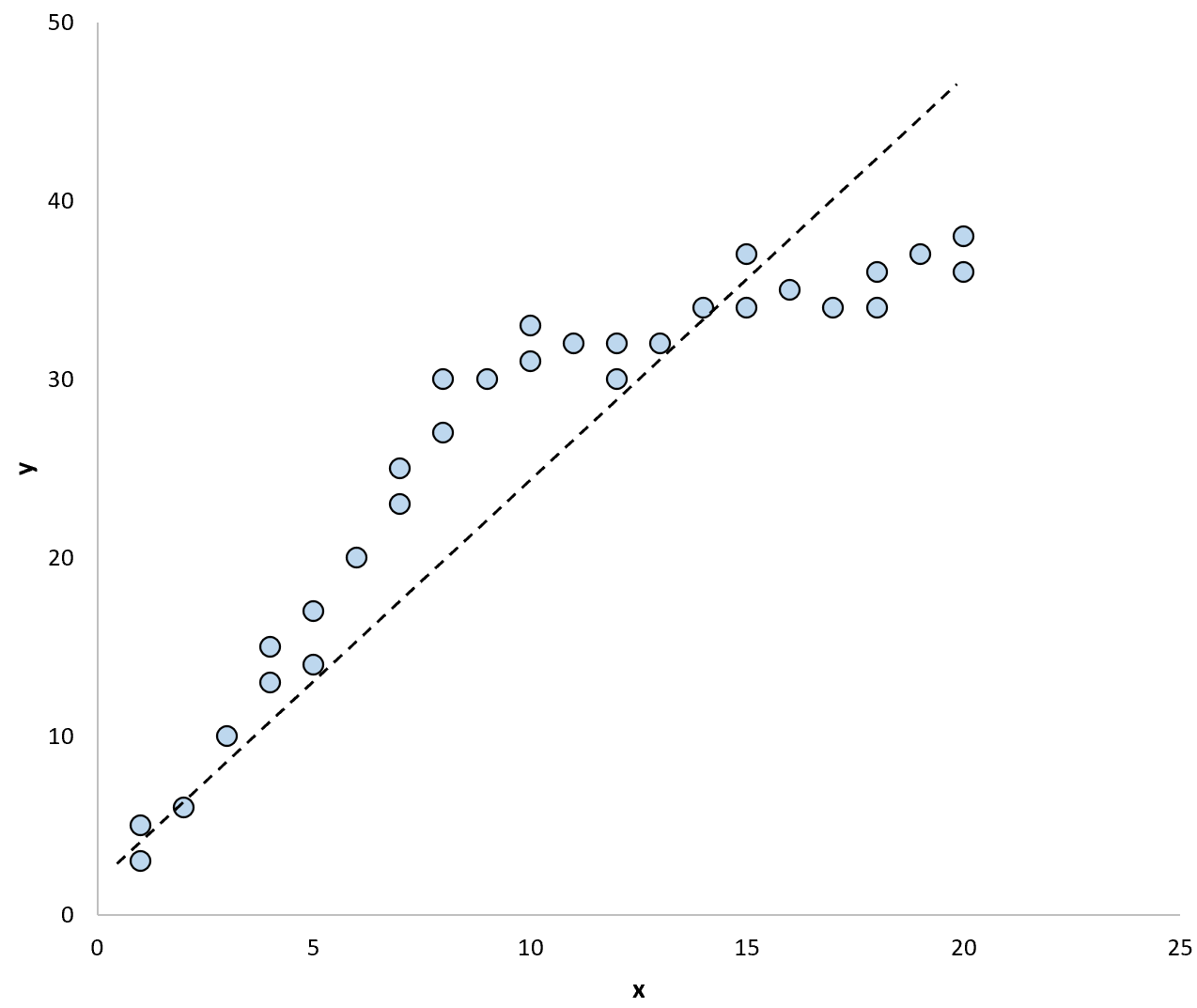
回帰直線を使用してデータ内のモデルを要約すると、次のようになります。
2 つの別々の回帰直線を使用してデータ内のモデルを要約すると、次のようになります。
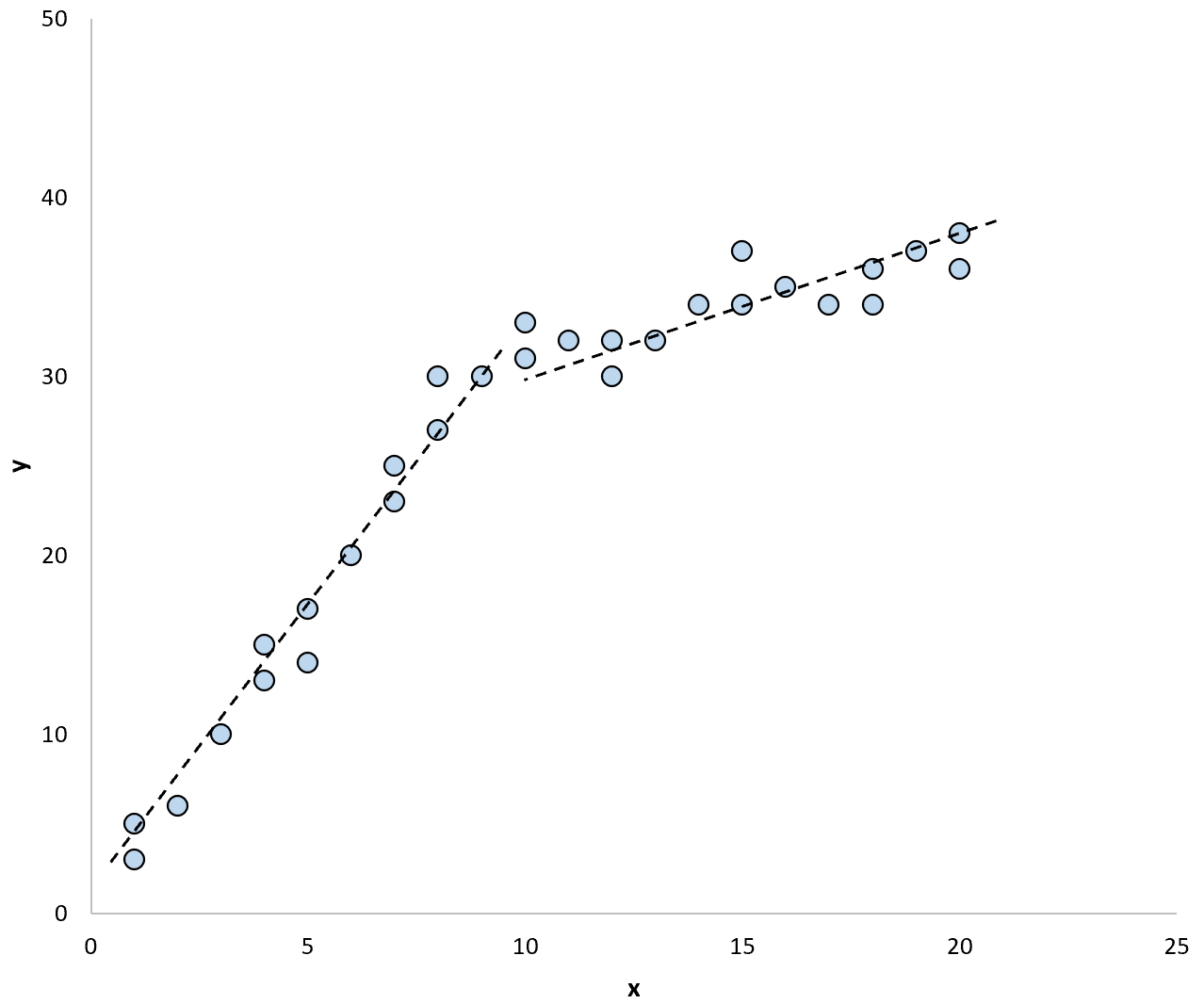
チャウ検定を使用すると、各回帰直線の回帰係数が等しいかどうかを検定できます。
テストで回帰直線間の係数が等しくないことが判明した場合、これはデータに構造的破損の重大な証拠があることを意味します。言い換えれば、この構造的ブレークポイントの前後では、データの傾向が大きく異なります。
チャウテストをいつ使用するか
次の例は、チャウ テストを実行する必要がある状況を示しています。
1.選挙の前後で株価の変動率が異なるかどうかを判断します。
2.金利変更の前後で住宅価格が変化するかどうかを判断します。
3.公営企業の平均利益が新しい税法の採用前後で異なるかどうかを判断します。
それぞれの状況で、Chow テストを使用して、特定の時点でデータに構造的なブレークポイントがあるかどうかを判断できます。
固形飼料検査を実行する手順
次の手順を使用して、チャウテストを実行できます。
ステップ 1: 帰無仮説と対立仮説を定義します。
次の回帰モデルをデータセット全体に当てはめるとします。
- y t = a + bx 1t + cx t2 + ε
次に、構造的なブレークポイントに基づいてデータを 2 つのグループに分割し、次の回帰モデルを各グループに当てはめるとします。
- y t = a 1 + b 1 x 1t + c 1 x t2 + ε
- y t = a 2 + b 2 x 1t + c 2 x t2 + ε
Chow 検定には次の帰無仮説と対立仮説を使用します。
- Null (H 0 ): a 1 = a 2 、b 1 = b 2および c 1 = c 2
- 代替 (H A ): Null の比較の少なくとも 1 つが等しくありません。
帰無仮説を棄却した場合、データに構造的なブレークポイントが存在し、1 つの回帰直線よりも 2 つの回帰直線の方がデータによく適合すると言える十分な証拠があることになります。
帰無仮説を棄却できなかった場合、データに構造的なブレークポイントがあると言える十分な証拠がありません。この場合、回帰直線は、データのパターンを十分に表す単一の回帰直線に「まとめる」ことができると言えます。
ステップ 2: 検定統計量を計算します。
次の用語を定義すると:
- S T :全データの残差の二乗和
- S 1 、S 2 : 各グループの残差の二乗和
- N 1 、 N 2 :各グループの観測値の数
- k:パラメータの数
したがって、チャウ検定統計量は次のようになります。
チョウ検定統計量 = [(S T – (S 1 +S 2 ))/k] / [(S 1 +S 2 )/ (N 1 +N 2 -2k)]
この検定統計量は、 kおよび N 1 +N 2 -2k の自由度を持つ F 分布に従います。
ステップ 3: 帰無仮説を棄却するか、棄却しません。
この検定統計量に関連付けられた p 値が特定の有意水準を下回っている場合、帰無仮説は棄却され、データに構造的なブレークポイントがあると結論付けることができます。
幸いなことに、ほとんどの統計ソフトウェアはチャウテストを実行できるため、テストを手動で実行する必要はおそらくありません。
チャウテストの実施例
R で特定のデータセットに対して Chow テストを実行する方法の段階的な例を確認するには、このチュートリアルを参照してください。
チョウテストノート
Chow テストに関して留意すべき注意事項がいくつかあります。
1.このテストでは、回帰モデルの残差が分散が未知の正規分布から独立して同一に分布すると仮定します。
2.チャウテストは、テストしたい構造破壊が既知の時間に発生する場合にのみ使用してください。言い換えれば、特定の瞬間が構造的破損とみなせるかどうかを判断するためにテストを繰り返し使用するべきではありません。