Anova における高い f 値は何を意味しますか?
一元配置分散分析は、 3 つ以上の独立したグループの平均が等しいかどうかを判断するために使用されます。
一元配置分散分析では、次の帰無仮説と対立仮説が使用されます。
- H 0 :すべてのグループ平均が等しい。
- H A :少なくとも 1 つのグループの平均が他のグループの平均とは異なります。
一元配置分散分析を実行するたびに、次のような要約表が作成されます。
| ソース | 二乗和 (SS) | DF | 平均二乗 (MS) | F | P値 |
|---|---|---|---|---|---|
| 処理 | 192.2 | 2 | 96.1 | 2,358 | 0.1138 |
| エラー | 1100.6 | 27 | 40.8 | ||
| 合計 | 1292.8 | 29 |
表中のF 値は次のように計算されます。
- F 値 = 平均二乗処理 / 平均二乗誤差
これを別の方法で書くと次のようになります。
- F 値 = サンプル平均間の変動 / サンプル内の変動
サンプル平均間の変動が各サンプル内の変動と比較して大きい場合、F 値は大きくなります。
たとえば、上の表の F 値は次のように計算されます。
- F値 = 96.1 / 40.8 = 2.358
この F 値に対応するp 値を見つけるには、分子の自由度 = df 処理、分母の自由度 = df 誤差を指定したF 分布計算機を使用できます。
たとえば、F 値 2.358、分子 df = 2、分母 df = 27 に対応する p 値は0.1138です。
この p 値は α = 0.05 以上であるため、帰無仮説を棄却できません。これは、3 つのグループの平均値の間に統計的に有意な差がないことを意味します。
ANOVA の F 値を表示する
ANOVA 表の F 値を直感的に理解するために、次の例を考えてみましょう。
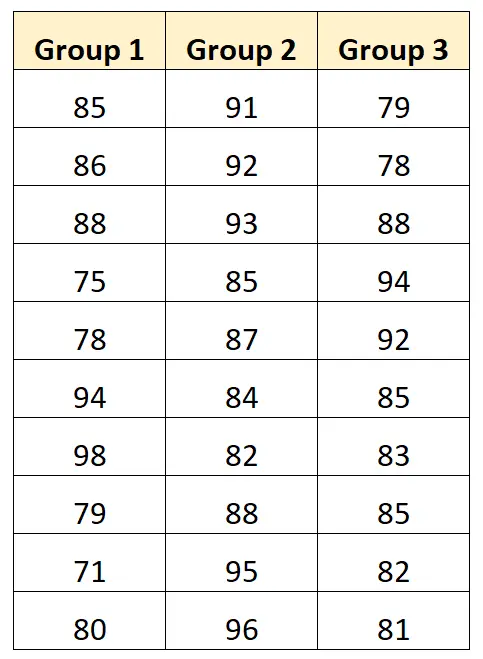
一元配置分散分析を実行して、3 つの異なる勉強法が異なる試験の平均点を生み出すかどうかを判断したいとします。次の表は、各テクニックを使用した 10 人の学生の試験結果を示しています。
次のグラフを作成して、グループごとに試験結果を視覚化できます。
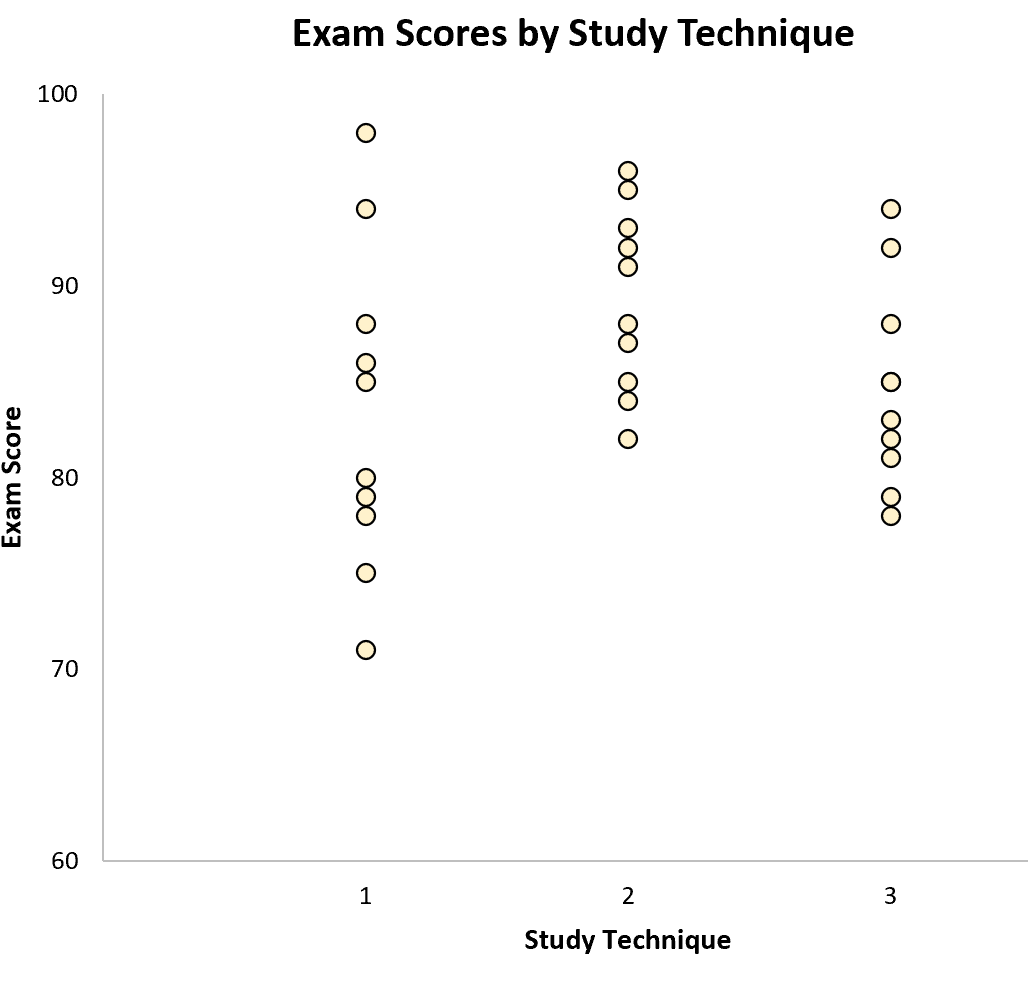
サンプル内の変動は、個々のサンプル内の値の分布によって表されます。
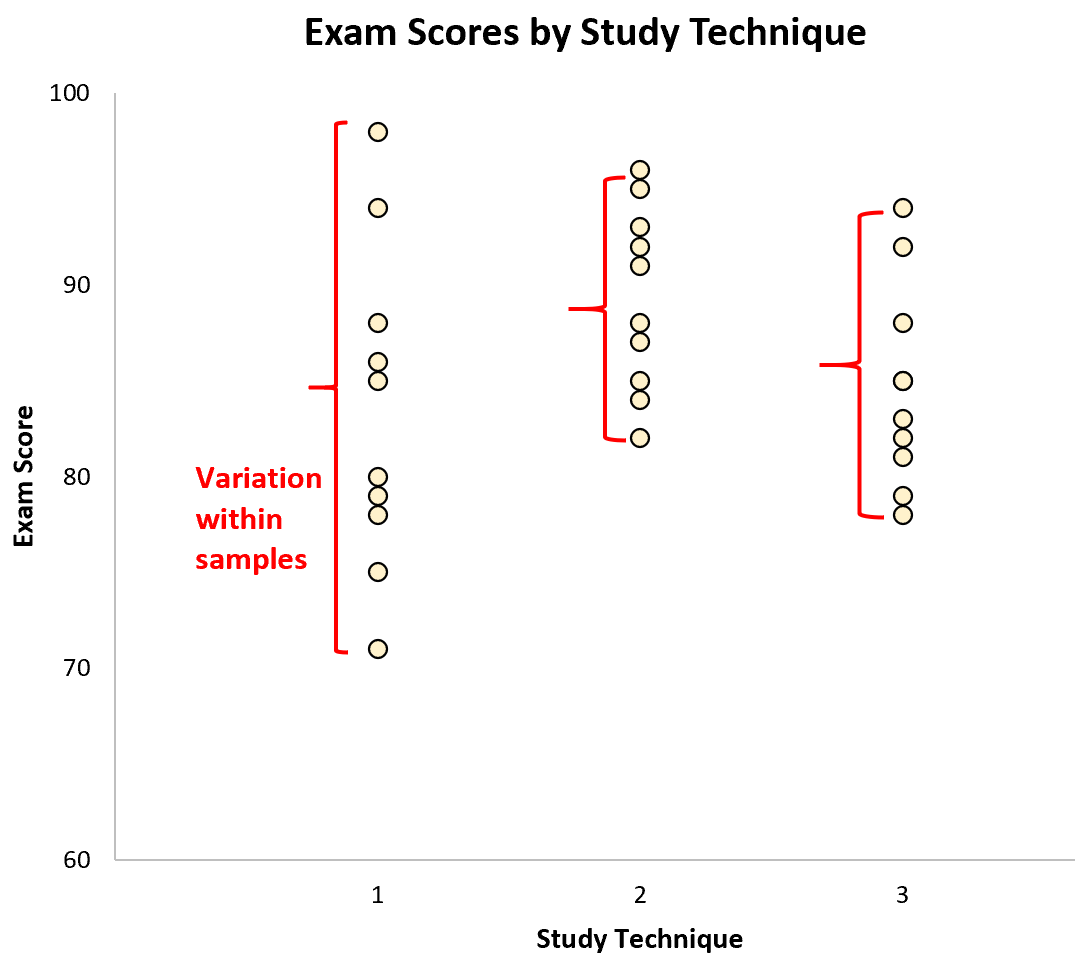
サンプル間の変動は、サンプル平均間の差によって表されます。
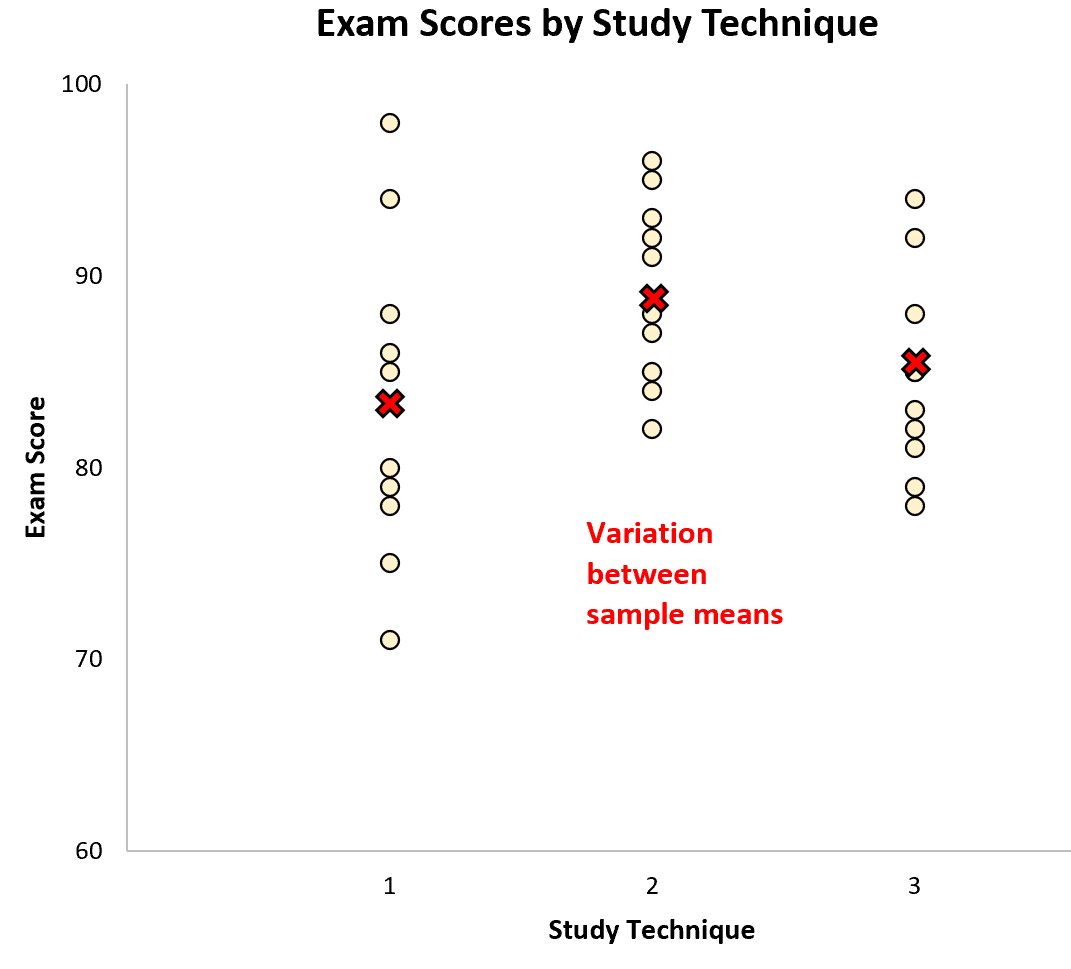
このデータセットに対して一元配置分散分析を実行すると、F 値が2.358で、対応する p 値が0.1138であることがわかります。
この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。これは、使用した学習手法によって試験の平均点に統計的に有意な差が生じたと言える十分な証拠がないことを意味します。
言い換えれば、これは、標本平均間のばらつきが、標本内のばらつきに比べて帰無仮説を棄却できるほど大きくないことを示しています。
結論
この記事の要点を簡単に要約すると次のとおりです。
- ANOVA の F 値は、サンプル平均間の変動 / サンプル内の変動として計算されます。
- ANOVA の F 値が高くなるほど、サンプル内の変動に比べてサンプル平均間の変動が大きくなります。
- F 値が高くなるほど、対応する p 値は低くなります。
- p 値が特定のしきい値 (例: α = 0.05) を下回っている場合、ANOVA の帰無仮説を棄却し、グループ平均間に統計的に有意な差があると結論付けることができます。