ポアソン分布の概要

ポアソン分布は、統計学で最もよく使われる分布の 1 つです。

ポアソン分布を理解するには、まずポアソン実験を理解することが役立ちます。

魚の実験

ポアソン実験は、次の特性を持つ実験です。

• 実験の成功回数をカウントすることができます。
• 特定の時間 (または空間) 間隔中に発生した成功の平均数がわかっています。
• それぞれの結果は独立しています。
• 成功する確率は間隔のサイズに比例します。

ポアソン実験の例としては、特定の病院における 1 時間あたりの出生数が挙げられます。たとえば、特定の病院で 1 時間あたり平均 10 件の出産が行われているとします。次の 4 つの特性があるため、これはポアソン実験です。

• 実験の成功数は数えられます – 出生数も数えられます。
• 特定の期間中に発生する平均出産数はわかっています。1 時間あたり平均 10 件の出産があることがわかっています。
• それぞれの結果は独立しています – ある母親が特定の時間内に出産する確率は、別の母親が出産する確率とは独立しています。
• 成功が起こる確率は間隔の大きさに比例します。時間間隔が長いほど、出産が起こる確率は高くなります。

ポアソン分布を使用すると、このポアソン実験に関する確率に関する次のような質問に答えることができます。

• 一定時間に 12 件以上の出産が起こる確率はどれくらいですか?
• 特定の時間に 5 件未満の出生が発生する確率はどれくらいですか?
• 指定された時間に 8 人から 11 人の間で出産が起こる確率はどれくらいですか?

魚の分布

ポアソン分布は、指定された時間間隔中にk回の成功が得られる確率を表します。

確率変数X がポアソン分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = λ ^k * e ^{– λ} / k!

金：

• λ:特定の間隔中に発生した成功の平均数
• k:成功回数
• e:約 2.71828 に等しい定数

たとえば、特定の病院で 1 時間あたり平均 2 件の出産があったとします。上記の式を使用して、0、1、2、3 回の出産などを経験する確率を決定できます。特定の時間内に:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0.1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0.2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0.2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0.1805

無限大までの任意の数の出生確率を計算できます。次に、この確率分布を視覚化するための単純なヒストグラムを作成します。

累積ポアソン確率の計算

上記の式を使用して単一のポアソン確率 (たとえば、病院で 1 時間に 3 件の出産が発生する確率) を計算するのは簡単ですが、累積ポアソン確率を計算するには、個々の確率を加算する必要があります。

たとえば、特定の時間に病院で出産が 1 件以下になる確率を知りたいとします。この確率を計算するには次の式を使用します。

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

複数の確率を加算する必要があるため、これは累積確率と呼ばれます。同様の式を使用して、特定の時間内にk以下の出生が発生する累積確率を計算できます。

P(X≤0) = P(X=0) = 0.1353

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767

これらの累積確率は、無限に至るまでの任意の数の出生について計算できます。次に、ヒストグラムを作成して、この累積確率分布を視覚化できます。

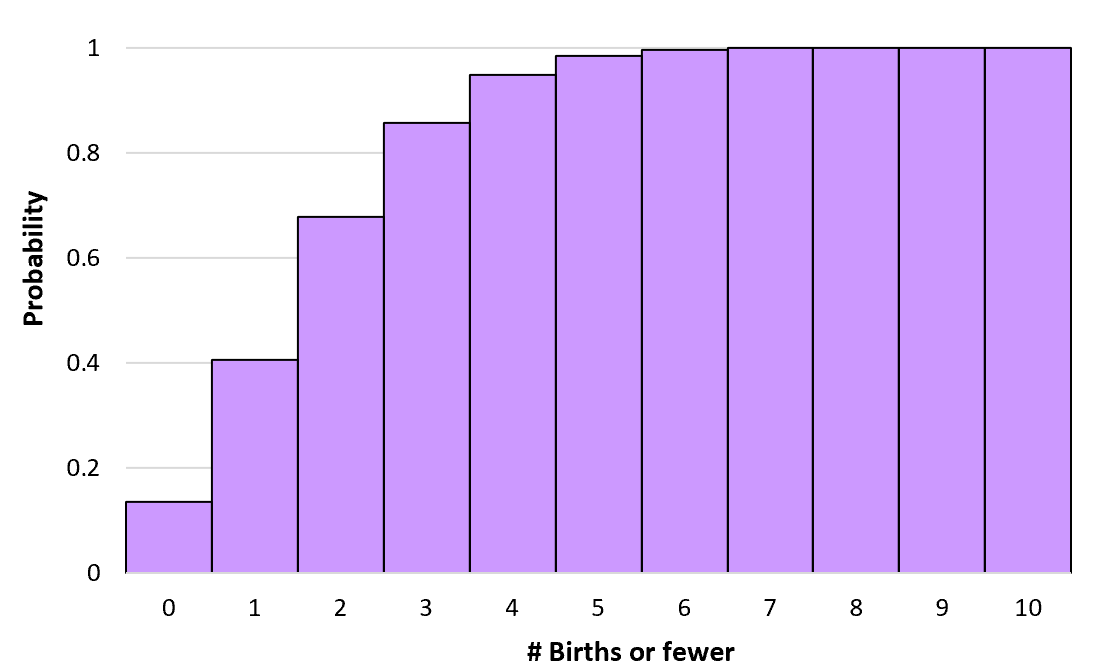
ポアソン分布の性質

ポアソン分布には次の特性があります。

分布の平均はλです。

分布の分散もλです。

分布の標準偏差は√ λです。

たとえば、ある病院では 1 時間あたり平均 2 件の出産が行われているとします。

特定の時間に予想される平均出生数は、λ = 2 回の出生です。

予想される出生数の分散は λ = 2 出生です。

魚の分布練習問題

次の練習問題を使用して、ポアソン分布の知識をテストしてください。

注:これらの質問に対する答えを計算するには、ポアソン分布計算ツールを使用します。

問題 1

質問:特定の Web サイトが 1 時間あたり 10 件の売上を上げていることがわかっています。指定された 1 時間に、サイトでちょうど 8 件の販売が行われる確率はどれくらいですか?

回答: λ = 10 および x = 8 でポアソン分布計算を使用すると、 P(X=8) = 0.1126であることがわかります。

問題 2

質問:ある不動産業者は月に平均 5 件の販売を行っていることがわかっています。特定の月に、彼女が 7 件以上の販売を行う確率はどれくらいですか?

回答: λ = 5 および x = 7 でポアソン分布計算を使用すると、 P(X>7) = 0.13337であることがわかります。

問題 3

質問:ある病院では 1 時間あたり 4 件の出産が行われていることがわかっています。指定された時間内に、出生数が 4 人以下になる確率はどれくらいですか?

回答: λ = 4 および x = 4 でポアソン分布計算を使用すると、 P(X≤4) = 0.62884であることがわかります。

追加リソース

次の記事では、さまざまな統計ソフトウェアでポアソン分布を使用する方法について説明します。

R でポアソン分布を使用する方法
Excelでポアソン分布を使用する方法
TI-84 計算機でポアソン確率を計算する方法
ポアソン分布の実世界の例
魚の分布計算機