Python でポアソン分布を使用する方法

ポアソン分布は、指定された時間間隔中にk回の成功が得られる確率を表します。

確率変数X がポアソン分布に従う場合、 X = kが成功する確率は次の式で求められます。

P(X=k) = λ ^k * e ^{– λ} / k!

金：

• λ:特定の間隔中に発生した成功の平均数
• k:成功回数
• e:約 2.71828 に等しい定数

このチュートリアルでは、Python でポアソン分布を使用する方法を説明します。

ポアソン分布を生成する方法

Poisson.rvs(mu, size)関数を使用すると、特定の平均値とサンプル サイズを持つポアソン分布からランダムな値を生成できます。

 from scipy. stats import fish

#generate random values from Poisson distribution with mean=3 and sample size=10
fish. rvs (mu=3, size=10)

array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])

ポアソン分布を使用して確率を計算する方法

関数Poisson.pmf(k, mu)およびPoisson.cdf(k, mu)を使用して、ポアソン分布に関連する確率を計算できます。

例 1: 特定の値に等しい確率

店では 1 日に平均 3 個のリンゴが売れます。特定の日にリンゴが 5 個売れる確率はどれくらいですか?

 from scipy. stats import fish

#calculate probability
fish. pmf (k=5, mu=3)

0.100819

店で 1 日に 5 個のリンゴが売れる確率は0.100819です。

例 2: 一定の値未満の確率

ある店では1日平均7個のサッカーボールが売れる。この店で 1 日に販売されるサッカー ボールが 4 個以下になる確率はどれくらいですか?

 from scipy. stats import fish

#calculate probability
fish. cdf (k=4, mu=7)

0.172992

店舗が特定の日に販売するサッカー ボールが 4 個以下である確率は0.172992です。

例 3: 特定の値より大きい確率

ある店では1日平均15缶のツナ缶が売れる。この店で 1 日に 20 缶以上のツナ缶が売れる確率はどれくらいですか?

 from scipy. stats import fish

#calculate probability
1-fish. cdf (k=20, mu=15)

0.082971

店が 1 日に 20 缶以上のツナ缶を販売する確率は0.082971です。

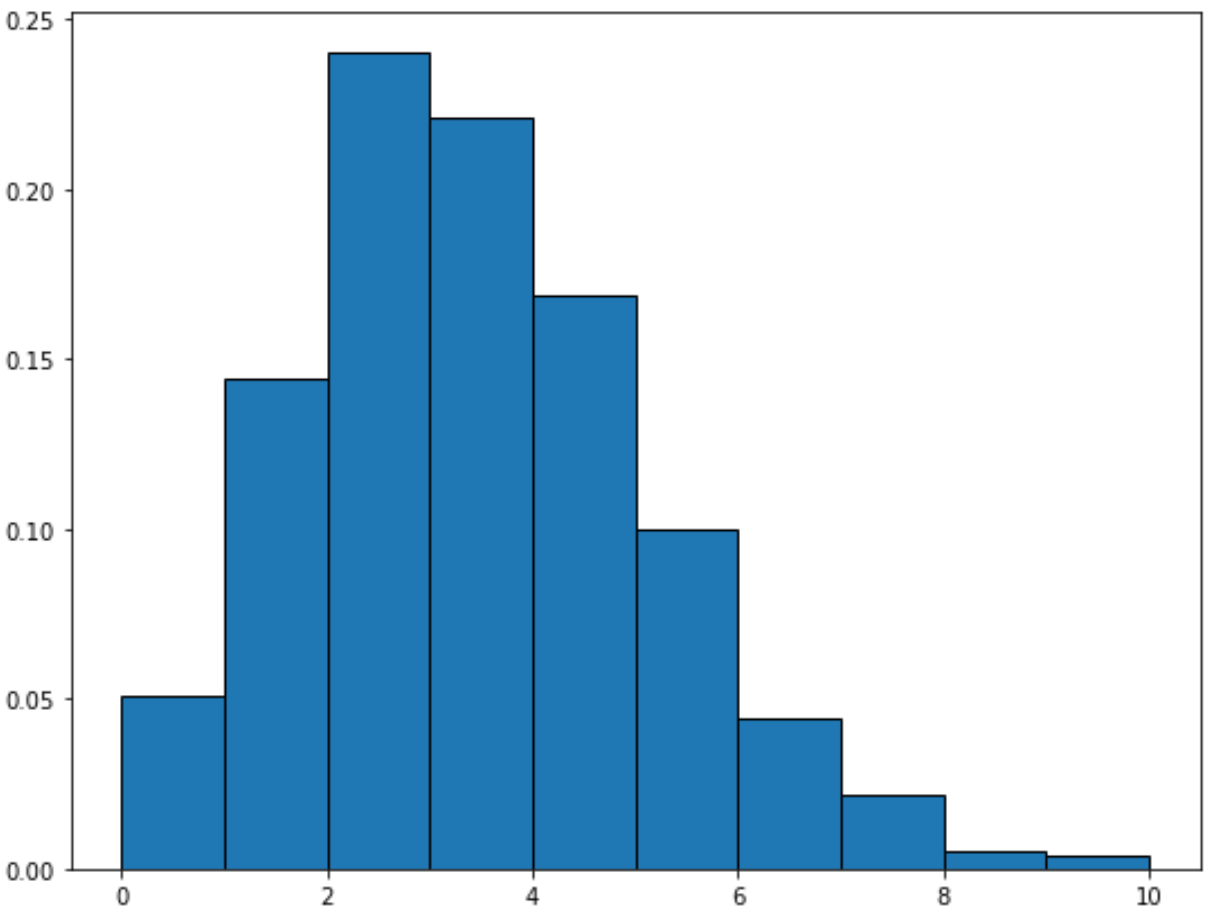
ポアソン分布をプロットする方法

次の構文を使用して、特定の平均値でポアソン分布をプロットできます。

 from scipy. stats import fish
import matplotlib. pyplot as plt

#generate Poisson distribution with sample size 10000
x = fish. rvs (mu=3, size=10000)

#create plot of Poisson distribution
plt. hist (x, density= True , edgecolor=' black ')

追加リソース

ポアソン分布の概要
ポアソン分布の 5 つの具体例
オンライン魚分布計算機