가중 평균
여기서는 가중평균이 무엇이고 어떻게 계산하는지 설명하겠습니다. 가중 평균을 찾는 방법에 대한 해결된 연습을 볼 수 있습니다. 게다가, 마지막에 있는 계산기를 사용하여 모든 데이터 세트의 가중 평균을 계산할 수 있습니다.
가중 평균은 무엇입니까?
가중 평균은 기술 통계의 중심성을 측정하는 것입니다. 가중 평균을 계산 하려면 먼저 각 통계 데이터에 해당 중량(또는 중량)을 곱한 다음 모든 제품을 더한 다음 마지막으로 가중 합계를 전체 가중치의 합으로 나누어야 합니다.
즉, 가중평균의 공식은 다음과 같습니다.

여기서 x i는 각 데이터 샘플을 나타내고 wi 는 해당 가중치를 나타냅니다.
따라서 데이터의 가중치가 높을수록 가중 평균 계산에 있어 해당 데이터의 중요성이 더욱 커집니다. 즉, 데이터의 가중치가 높을수록 가중 평균 결과에 더 많은 영향을 미칩니다.
가중 평균은 코스 중에 치르는 연습이나 시험을 다양한 중요성으로 평가할 수 있기 때문에 성적을 계산하는 데 특히 유용합니다. 가중평균은 인구의 물가를 측정하는 지표인 CPI(소비자물가지수)를 계산하는 데에도 사용된다.
가중평균 외에도 기하평균, 산술평균, 제곱평균, 조화평균 등 다른 유형의 평균도 있습니다.
가중 평균을 계산하는 방법
가중 평균을 계산하려면 다음 단계를 따라야 합니다.
- 각 통계 데이터에 해당 가중치를 곱합니다.
- 이전 단계에서 계산된 모든 제품을 더합니다.
- 위의 가중치 합계를 모든 가중치의 합계로 나눕니다.
- 얻은 결과는 통계 샘플의 가중 평균입니다.
👉 아래 계산기를 사용하여 모든 데이터 세트의 가중 평균을 계산할 수 있습니다.
가중평균의 예
가중 평균의 정의를 고려하여 이제 일련의 데이터에서 가중 평균을 얻는 방법을 완전히 이해하기 위한 연습 문제를 풀어보겠습니다.
- 고등학교 1학년 학생이 수학 과목에서 다음과 같은 성적을 받았습니다: 부분 시험에서 30%를 차지하는 7점, 그룹 활동에서 20%를 차지하는 9점, 수업 시간에 가중치를 부여하는 연습 문제에서 6점 10%, 최종 시험에서 8점을 받아 가중치가 40%입니다. 해당 과목의 최종 성적은 무엇입니까?
학생의 성적을 결정하려면 진술에서 주어진 값으로 가중 평균을 찾아야합니다. 이를 위해 가중 평균 공식을 적용합니다.
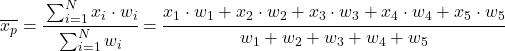
각 결과물의 점수는 통계적 값이며 그 백분율은 해당 값의 가중치에 해당합니다. 따라서 값과 가중치를 공식에 대체하고 가중 평균 계산을 수행합니다.
![]()
따라서 이 학생의 최종 수학 성적은 7.7이 될 것입니다. 이는 가중 평균으로 얻은 결과이기 때문입니다.
가중 평균 계산기
통계 샘플의 데이터와 해당 가중치를 아래 계산기에 입력하여 가중 평균을 계산하세요.
첫 번째 상자에는 통계 데이터를 입력하고 두 번째 상자에는 해당 가중치를 입력합니다. 가중치는 데이터와 동일한 순서로 소수점 형식으로 작성해야 합니다. 모든 숫자는 공백으로 구분해야 하며 마침표를 소수점 구분 기호로 사용하여 입력해야 합니다.
표준화된 가중치
앞서 살펴보았듯이 가중 평균에서 가중치는 각 데이터에 어느 정도 중요도를 부여하기 위해 부여되는 값입니다. 따라서 정보가 매우 중요한 경우에는 매우 높은 가중치를 가지게 되고, 그다지 관련성이 없는 정보인 경우에는 매우 낮은 가중치를 가지게 됩니다.
정규화된 가중치는 어떤 분할도 하지 않고 가중 평균을 구하는 데 사용되는 가중치 유형입니다.
정규화된 가중치는 데이터 항목의 가중치를 모든 가중치의 합으로 나눈 값입니다.
![]()
따라서 모든 정규화된 가중치의 합은 1과 같습니다.
![]()
따라서 정규화된 가중치를 사용하여 가중 평균을 계산 하려면 각 데이터 항목에 정규화된 가중치를 곱하면 됩니다.
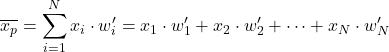
예를 들어, 데이터가 24, 35, 17, 41이고 각각의 가중치가 4, 9, 6, 3인 통계 샘플이 있습니다. 이 데이터 세트의 가중 평균을 찾으려면 먼저 나눔으로 정규화된 가중치를 계산할 수 있습니다. 각 가중치를 모든 가중치의 합으로 계산:
![]()
![]()
![]()
![]()
이제 각 데이터에 정규화된 가중치를 곱하면 결과가 가중 평균이 됩니다.
![]()
가중평균과 산술평균의 차이
가중평균과 산술평균의 계산도 유사한 연산을 수행해야 하므로 동일한 방식으로 수행됩니다. 가중 평균에서는 각 데이터 포인트에 가중치를 곱하고 가중치의 합으로 나누지만, 산술 평균에서는 모든 데이터를 더한 후 전체 데이터 포인트 수로 나눕니다.
가중평균과 산술평균의 차이는 개념에 있습니다. 산술평균에서는 모든 데이터가 동일한 값을 갖는 것으로 간주되지만 가중평균에서는 각 데이터의 가중치가 다르기 때문입니다.
모든 가중치가 동일하면 가중 평균은 산술 평균과 동일합니다. 아래에서 수학적 증명을 볼 수 있습니다.
![Rendered by QuickLaTeX.com \begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-16b06cfb0813f7f4fd755ea7bbf1bf00_l3.png)