베이즈의 정리

이 기사에서는 베이즈 정리가 무엇인지, 확률과 통계에서 어떤 용도로 사용되는지 설명합니다. 따라서 베이즈 정리의 공식이 무엇인지, 베이즈 정리의 해결 사례와 이 정리의 응용이 무엇인지 알게 됩니다.

베이즈의 정리란 무엇입니까?

확률 이론에서 베이즈 정리는 해당 사건에 대한 사전 정보가 알려진 경우 해당 사건의 확률을 계산하는 데 사용되는 법칙입니다.

보다 구체적으로, 베이즈 정리는 사건 B가 주어졌을 때 사건 A가 일어날 확률과 A가 주어졌을 때 B가 일어날 확률을 수학적으로 연관시킵니다.

예를 들어, 독감에 걸린 사람이 두통을 앓을 확률을 미리 알고 있다면 베이즈 정리를 사용하여 두통이 있을 때 독감에 걸릴 확률을 결정할 수 있습니다.

베이즈 정리는 많은 응용 분야를 가지고 있습니다. 예를 들어 의학, 경제학 또는 기술에서 다른 사건에 의해 조건화된 특정 사건의 확률을 계산하는 데 사용됩니다. 아래에서는 베이즈 정리의 다양한 응용에 대해 자세히 살펴보겠습니다.

베이즈 정리는 영국의 수학자 토마스 베이즈(1702-1761)가 창안했지만 사후 1763년에 출판되었습니다.

베이즈 정리의 공식

베이즈 정리에 따르면 확률이 0이 아닌 상호 배타적인 사건 집합 {A ₁ , A ₂ ,…, A _i ,…, _An }과 또 다른 사건 B로 구성된 표본 공간이 주어지면 조건식을 수학적으로 연관시킬 수 있습니다. 사건 B가 주어졌을 때 A _i 의 확률과 A _i가 주어졌을 때 B의 조건부 확률.

따라서 베이즈 법칙 이라고도 알려진 베이즈 정리 의 공식은 다음과 같습니다.

금:

• 

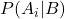
  는 사건 B가 주어졌을 때 사건 A _i 의 조건부 확률이며 사후 확률이라고 합니다.

• 

  는 사건 A _가 주어졌을 때 사건 B의 조건부 확률입니다.

• 

  는 사건 A _가 발생할 확률이며 사전 확률이라고 합니다.

베이즈 정리 공식의 분모는 사건 B의 총 확률 입니다.

베이즈 정리의 예

베이즈 정리의 정의와 공식이 무엇인지 알아보고 나면, 개념을 더 잘 이해할 수 있도록 베이즈 정리로 확률을 계산하는 방법에 대한 해결 사례를 살펴보겠습니다.

• 한 전자제품 매장에서 X, Y, Z라는 세 가지 브랜드의 TV를 판매하고 있습니다. 매출의 20%는 브랜드 TV에 결함이 있고, 브랜드 Y TV의 3%는 결함이 있으며, 브랜드 Z TV의 4%는 결함이 있는 것으로 추정됩니다. 결함이 있는 TV가 있는 경우 해당 TV가 브랜드 Z TV일 확률은 얼마입니까?

이 연습을 통해 고객이 각 브랜드의 TV를 구매할 확률을 알 수 있습니다.

• 사건 A ₁ : 고객이 X 브랜드 텔레비전을 구매함 → P(A ₁ )=0.20
• 사건 A ₂ : 고객이 Y 브랜드 텔레비전을 구입 → P(A ₂ )=0.50
• 사건 A ₃ : 고객이 브랜드 Z 텔레비전을 구매함 → P(A ₃ )=0.30

또한 이 판독값은 각 브랜드의 TV에 결함이 있을 확률도 제공합니다.

사건 B: TV에 결함이 있습니다

• B|A ₁ : 브랜드 X 텔레비전이 주어지면 텔레비전에 결함이 있음 → P(B|A ₁ )=0.05
• B|A ₂ : 브랜드 Y 텔레비전이 주어지면 텔레비전에 결함이 있음 → P(B|A ₂ )=0.03
• B|A ₃ : 브랜드 Z 텔레비전이 주어지면 텔레비전에 결함이 있습니다 → P(B|A ₃ )=0.04

따라서 우리가 관심을 갖는 모든 사건의 확률 트리는 다음과 같습니다.

따라서 결함이 있는 텔레비전이 있을 때 브랜드 Z일 확률을 계산하려면 베이즈 정리의 공식을 사용해야 합니다.

이 예에 사용된 용어를 사용하면 Bayes의 공식은 다음과 같습니다.

따라서 결함이 있는 특정 TV가 브랜드 Z일 확률은 다음과 같이 계산됩니다.

결론적으로, TV에 결함이 있을 경우 Z 브랜드일 확률은 32%입니다.

베이즈 정리의 응용

베이즈 정리는 다음과 같은 다양한 응용 분야에 적용됩니다.

1. 의료 테스트 : 베이즈 정리는 진단 테스트를 통과할 확률을 결정하기 위해 의학에서 자주 사용됩니다. 예를 들어, HIV 테스트의 경우, 테스트 결과가 양성인 경우 해당 사람이 실제로 바이러스에 감염되었을 확률을 계산하는 데 정리를 사용할 수 있습니다.
2. 재무 분석 : 금융에서는 베이즈 정리를 사용하여 일련의 경제 변수에 따라 주가 상승 또는 하락과 같은 특정 경제적 사건이 발생할 확률을 계산합니다.
3. 시장 조사 : 베이즈 정리를 사용하면 예를 들어 사람이 이 제품에 대한 광고를 본 후 해당 제품을 구매할 확률을 결정할 수 있습니다.
4. 일기예보 : 날씨 모델은 베이즈 정리를 사용하여 관측된 데이터를 기반으로 한 특정 일기예보가 실현될 확률을 결정합니다. 이는 기후 예측의 정확성을 향상시킵니다.
5. 컴퓨터 보안 – 사이버 보안에서는 베이즈의 정리를 적용하여 의심스러운 활동이 실제로 컴퓨터 시스템에 대한 공격일 가능성을 판단할 수 있습니다.

해결 베이즈 정리 문제

연습 1

인구의 1%가 어떤 질병을 앓고 있는 것으로 추산됩니다. 이 질병을 탐지하는 테스트는 양성 사례의 경우 95% 정확하고 음성 사례의 경우 90% 정확합니다. 무작위로 선택된 사람이 양성 반응을 보인다면 그 사람이 실제로 질병에 걸렸을 확률은 얼마나 됩니까?

운동 진술은 다음과 같은 확률을 제공합니다.

A ₁ : 질병을 갖고 있는 사람 → P(A ₁ )=0.01
A ₂ : 질병이 없는 사람 → P(A ₂ )=0.99

B: 테스트 결과가 양성입니다.
B|A ₁ : 질병이 있는 경우 양성 → P(B|A ₁ )=0.95
B|A ₂ : 질병이 없는 경우 양성 → P(B|A ₂ )=1-0.90=0.10

그런 다음, 무작위로 선택된 사람이 양성 판정을 받았을 때 실제로 질병에 걸릴 확률을 계산하려면 베이즈 규칙을 적용해야 합니다.

따라서 값을 공식에 대입하고 확률 계산을 수행합니다.

즉, 무작위로 선택된 사람이 양성 판정을 받고 실제로 질병에 걸릴 확률은 8.76%입니다.

연습 2

하루 만에 주가가 상승할 확률은 40%, 안정적으로 유지될 확률은 10%, 하락할 확률은 50%로 추정된다. 또한, 우리는 시장이 상승할 때 재무 분석가가 이를 정확하게 예측할 확률이 90%이고, 시장이 안정적일 때 예측이 정확할 확률은 75%이며, 하락할 경우에는 정확한 예측 확률은 75%입니다. 85%.%. 분석가가 시장이 하락할 것이라고 예측한다면 실제로 하락할 가능성은 얼마나 됩니까?

이 경우 운동 명령문은 다음과 같은 확률을 제공합니다.

A ₁ : 시장이 하루 만에 상승 → P(A ₁ )=0.40
A ₂ : 시장은 하루 동안 안정 상태를 유지 → P(A ₂ )=0.10
A ₃ : 시장이 하루 만에 상승 → P(A ₃ )=0.50

B: 분석가는 시장이 하락할 것이라고 예측합니다.
B|A ₁ : 분석가는 시장이 상승할 것이라고 정확하게 예측했습니다 → P(B|A ₁ )=0.90
B|A ₂ : 분석가는 시장이 안정적으로 유지된다고 정확하게 예측합니다 → P(B|A ₂ )=0.75
B|A ₃ : 분석가는 시장이 하락할 것이라고 정확하게 예측했습니다 → P(B|A ₃ )=0.85

분석가가 시장이 하락할 것이라는 예측을 하고 그 예측이 정확할 확률을 확인하려면 베이즈 정리 공식을 사용해야 합니다.

확률 값을 베이즈 공식에 대입하고 확률을 계산합니다.

따라서 애널리스트가 주식시장이 하락할 것이라는 예측이 맞을 확률은 49.42%이다.