유통 기능

에 의해 벤자민 앤더슨 8월 5, 2023 개연성 댓글 0개

이 기사에서는 분포 함수에 대한 설명, 해당 값이 계산되는 방법 및 분포 함수의 실제 예를 찾을 수 있습니다. 또한 분포 함수와 밀도 함수의 차이점을 확인할 수 있습니다.

분포 함수란 무엇입니까?

누적 분포 함수라고도 하는 분포 함수 는 분포의 누적 확률을 나타내는 수학 함수입니다. 즉, 임의의 값에 대한 분포 함수의 이미지는 변수가 해당 값 또는 더 낮은 값을 취할 확률과 같습니다.

누적 분포 함수는 약어 FDA로 참조될 수도 있지만 일반적인 기호는 대문자 F입니다.

따라서 분포 함수는 다음 공식으로 정의됩니다.

$F(x)=P[X\leq x]$

분포함수를 계산하는 방법

그런 다음 확률 분포가 이산형인지 연속형인지에 따라 분포 함수의 값을 계산하는 방법을 설명합니다.

신중한 상자

확률 변수가 이산형인 경우 누적 분포 함수는 x 와 같거나 작은 모든 값의 확률의 합과 같습니다.

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

금

$f(u)$

이산변수와 연관된 확률 함수입니다.

계속되는 사건

확률 변수가 연속형인 경우 누적 분포 함수는 음의 무한대에서 문제의 값까지 밀도 함수를 적분한 것과 같습니다.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

금

$f(u)$

연속 변수와 관련된 밀도 함수입니다.

분포 함수 예

이제 분포 함수의 정의를 알았으니, 분포 함수 값을 계산하는 방법을 알아보기 위해 실제 단계별 예제를 살펴보겠습니다.

동전을 네 번 던지는 무작위 실험의 분포 함수를 계산합니다.

이 문제를 해결하려면 먼저 네 번의 동전 던지기 동안 앞면이 나올 확률과 관련된 모든 확률을 계산해야 합니다.

따라서 이산형 변수이기 때문에 분포 함수의 이미지를 결정하려면 해당 변수의 값에 확률을 더하는 것으로 충분합니다.

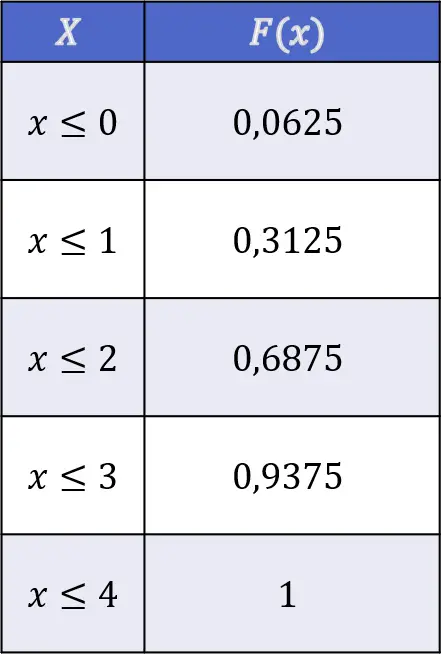
$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

따라서 4개의 독립된 동전을 던져 머리 뒤집기의 분포 함수 값은 다음과 같습니다.

분포함수의 속성

변수 유형에 관계없이 분포 함수는 항상 다음과 같은 속성을 갖습니다.

누적 분포 함수의 값은 0에서 1 사이입니다.

$0\leq F(x) \leq 1$

x가 무한대에 가까워지는 분포 함수의 극한은 1과 같습니다.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

반면, x가 음의 무한대에 접근할 때 분포 함수의 극한은 0입니다.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

그 특성상 분포 함수는 단조롭고 감소하지 않습니다.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

게다가 만약에
$a\leq b$

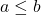
다음 방정식이 만족됩니다.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

분포함수와 밀도함수

마지막으로 분포 함수와 밀도 함수의 차이점이 무엇인지 살펴보겠습니다. 이 두 가지 통계적 개념은 종종 혼동되기 때문입니다.

분포 함수와 밀도 함수의 차이점은 그들이 정의하는 확률 유형입니다. 밀도 함수는 변수가 특정 값을 가질 확률을 설명하고, 분포 함수는 변수의 누적 확률을 설명합니다.

즉, 분포함수는 변수가 특정 값 이하일 확률을 계산하는 데 사용됩니다.

밀도 함수는 연속 변수만 참조하므로 이러한 구별은 연구 중인 변수가 연속인 경우에만 의미가 있습니다.

평균이 1이고 표준편차가 0.5인 정규 분포를 따르는 변수의 밀도 함수와 비교하여 분포 함수의 그래픽 표현이 어떻게 변경되는지 확인하세요.

밀도 함수에 대해 자세히 알아보려면 다음 문서를 참조하세요.

➤ 참조: 밀도 함수

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기