정규분포 또는 균일분포: 차이점은 무엇인가요?

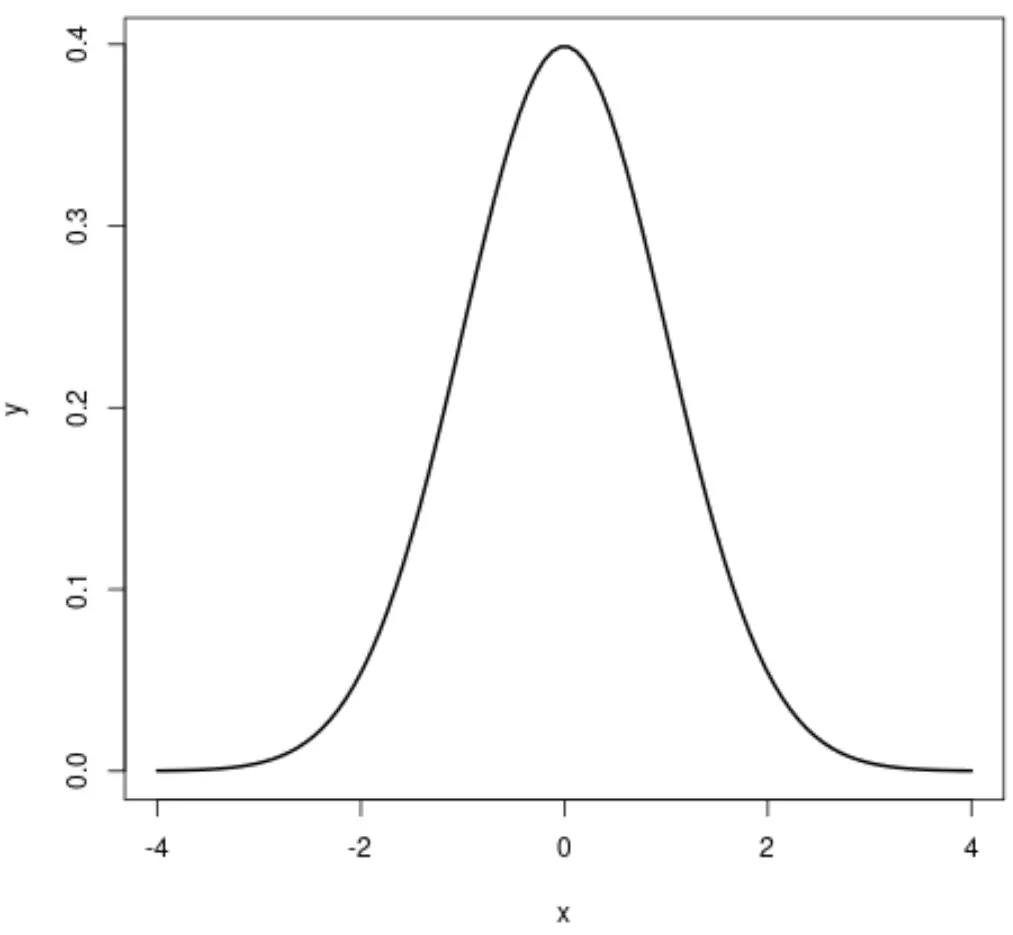
정규분포는 통계학에서 가장 일반적으로 사용되는 확률분포이다.

여기에는 다음과 같은 속성이 있습니다.

• 대칭
• 종 모양

정규분포 그래프를 그려보면 다음과 같습니다.

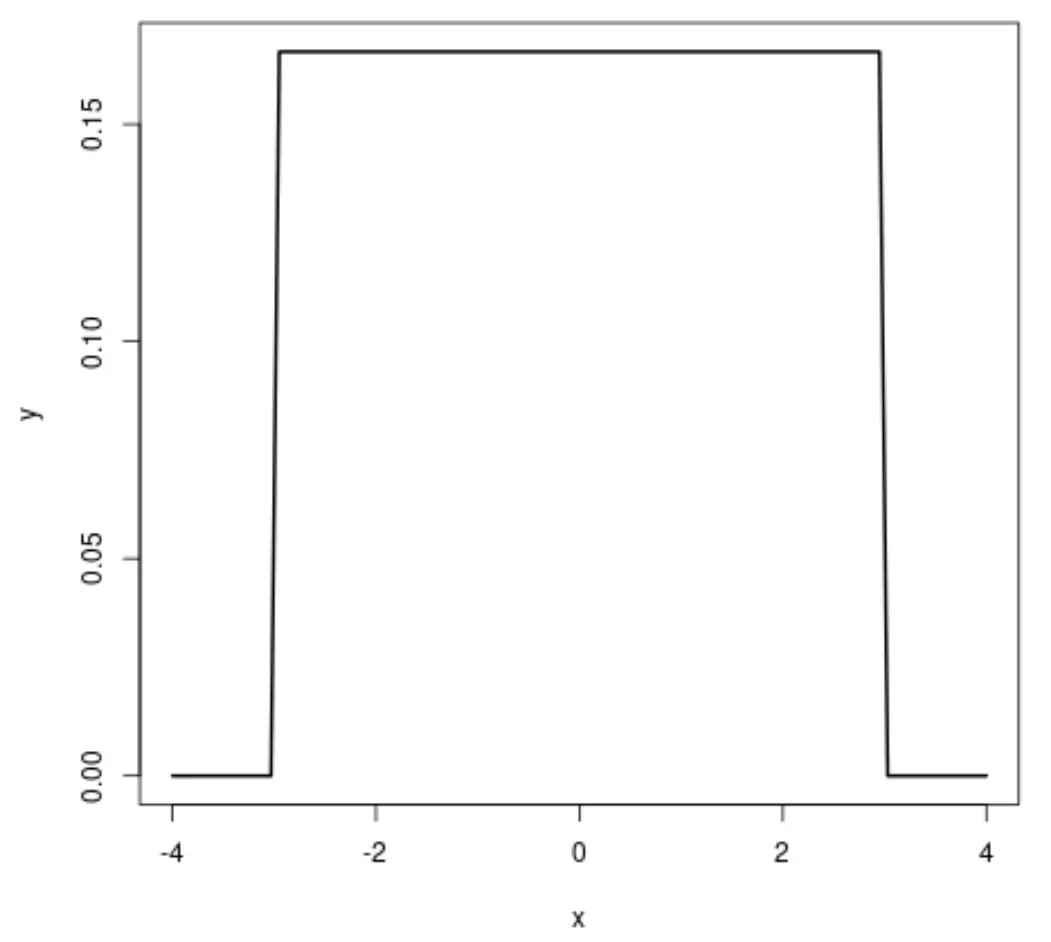
균일 분포는 a 에서 b까지 의 구간 사이의 각 값이 동일한 확률로 나타나는 확률 분포입니다.

여기에는 다음과 같은 속성이 있습니다.

• 대칭
• 직사각형 모양

균일 분포의 플롯을 작성하면 다음과 같습니다.

정규 분포와 균등 분포는 다음과 같은 유사점을 공유합니다.

• 두 분포는 대칭입니다. 즉, 분포의 중심을 통과하는 선을 그리면 분포의 왼쪽과 오른쪽이 서로 완벽하게 대칭됩니다.

그러나 두 분포에는 다음과 같은 차이점이 있습니다.

• 분포의 모양은 다양합니다.
• 정규 분포는 종 모양입니다. 즉, 분포 중앙에 가까운 값이 분포 꼬리에 있는 값보다 발생할 가능성이 더 높습니다.
• 균일 분포는 모양이 직사각형입니다. 이는 분포의 각 값이 동일한 발생 확률을 가짐을 의미합니다.

정규 분포 또는 균일 분포: 언제 사용합니까?

정규 분포는 “종형 곡선” 모양을 따르는 경향이 있는 현상을 모델링하는 데 사용됩니다. 예를 들어, 신생아의 출생 체중은 일반적으로 평균 약 7.5파운드로 분포된다는 것이 잘 기록되어 있습니다.

미국 신생아의 출생 체중 히스토그램은 일반적으로 정규 분포에 해당하는 종 모양을 표시합니다.

대부분의 아기의 체중은 약 7.5파운드이며, 일부는 7파운드 미만이고 일부는 8파운드를 초과합니다.

반대로, 균일 분포는 각 잠재적 결과가 동일할 가능성이 있는 시나리오를 모델링하는 데 사용됩니다.

전형적인 예는 주사위를 굴리는 것입니다. 주사위를 한 번 굴리면 1에서 6 사이의 숫자가 나올 확률은 각 숫자가 나올 확률이 동일하기 때문에 균일한 분포를 따릅니다.

예를 들어 주사위가 나올 수 있는 숫자는 6개이므로 1이 나올 확률은 1/6입니다.

마찬가지로 2가 나올 확률은 1/6입니다.

마찬가지로 3이 나올 확률은 1/6입니다.

등등.

보너스: 정규 분포와 균일 분포를 그리는 방법

R에서 다음 코드를 사용하여 정규 분포와 균일 분포의 플롯을 만들었습니다.

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

추가 리소스

정규분포의 6가지 구체적인 예
균일 분포의 5가지 구체적인 예
대칭 분포: 정의 + 예