Qq 플롯을 사용하여 정규성을 확인하는 방법

“분위수-분위수”의 약자인 QQ 플롯은 데이터 세트가 잠재적으로 이론적 분포에서 나오는지 여부를 평가하는 데 사용됩니다.

대부분의 경우 이러한 유형의 도표는 데이터 세트가 정규 분포를 따르는지 여부를 확인하는 데 사용됩니다.

데이터가 정규 분포를 따르는 경우 QQ 플롯의 점은 직선 대각선에 놓이게 됩니다.

반대로, 그래프의 점이 직선 대각선에서 크게 벗어날수록 데이터 세트가 정규 분포를 따를 가능성이 줄어듭니다.

다음 예에서는 R에서 QQ 플롯을 생성하여 정규성을 확인하는 방법을 보여줍니다.

예 1: 정규 데이터에 대한 QQ 플롯

다음 코드는 200개의 관측값이 포함된 정규 분포 데이터 세트를 생성하고 R에서 데이터 세트에 대한 QQ 플롯을 생성하는 방법을 보여줍니다.

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create QQ plot
qqnorm(data)
qqline(data)

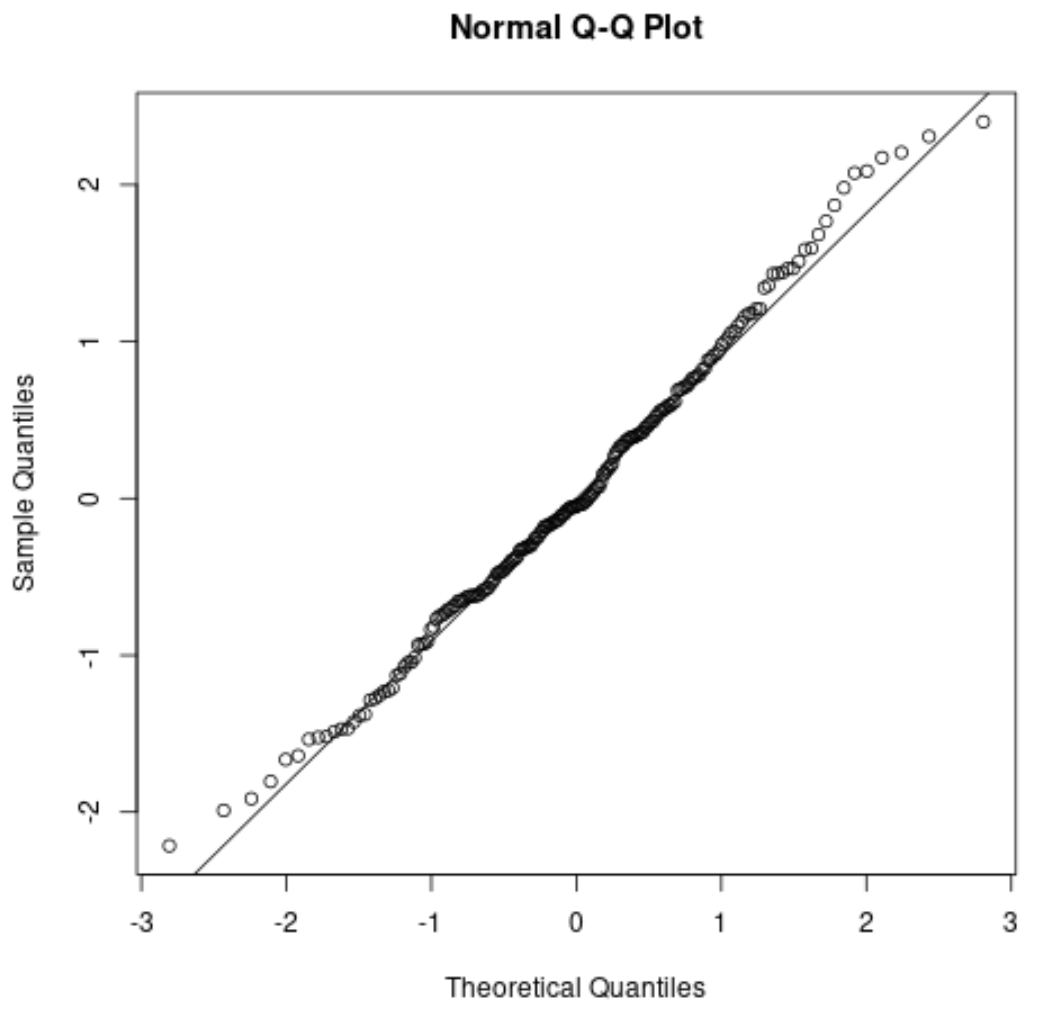
우리는 점들이 주로 직선 대각선을 따라 놓여 있고 각 꼬리를 따라 약간의 편차가 있음을 알 수 있습니다.

이 그래프를 기반으로 이 데이터세트가 정규 분포를 따른다고 안전하게 가정할 수 있습니다.

예 2: 비정규 데이터에 대한 QQ 플롯

다음 코드는 200개의 관측값이 있는 지수 분포를 따르는 데이터 세트에 대한 QQ 플롯을 만드는 방법을 보여줍니다.

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create QQ plot
qqnorm(data)
qqline(data)

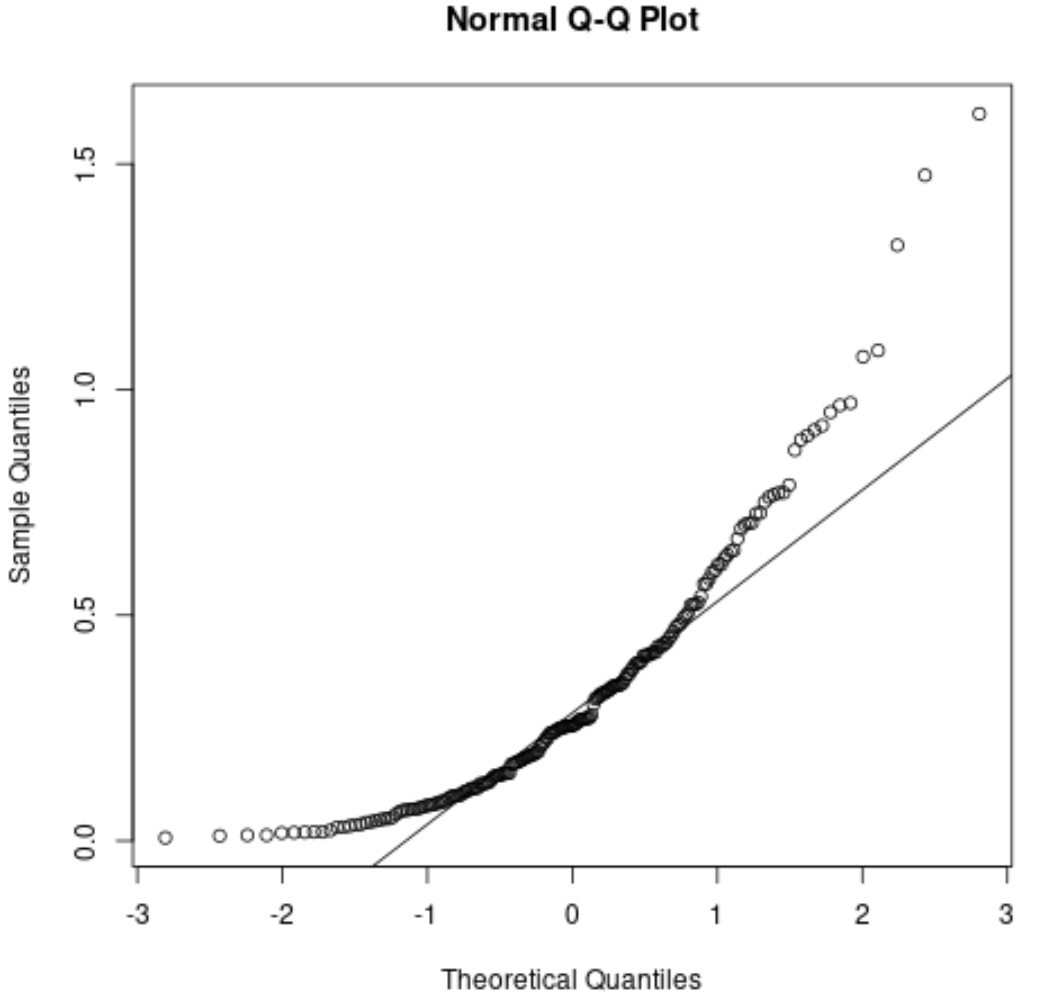
점들이 대각선에서 크게 벗어나는 것을 볼 수 있습니다. 이는 데이터 세트가 정규 분포를 따르지 않음을 분명히 나타냅니다.

데이터가 지수 분포를 따라야 한다고 지정했다는 점을 고려하면 이는 의미가 있습니다.

QQ 플롯 및 히스토그램

QQ 플롯은 데이터 세트가 정규 분포를 따르는지 여부를 시각적으로 확인하는 방법이라는 점에 유의해야 합니다.

정규성을 시각적으로 확인하는 또 다른 방법은 데이터 세트의 히스토그램을 만드는 것입니다. 데이터가 히스토그램에서 종형 곡선 모양을 대략적으로 따른다면 데이터 세트가 정규 분포를 따른다고 가정할 수 있습니다.

예를 들어, 이전에 정규 분포된 데이터 세트에 대한 히스토그램을 만드는 방법은 다음과 같습니다.

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create a histogram to visualize the distribution
hist(data) 

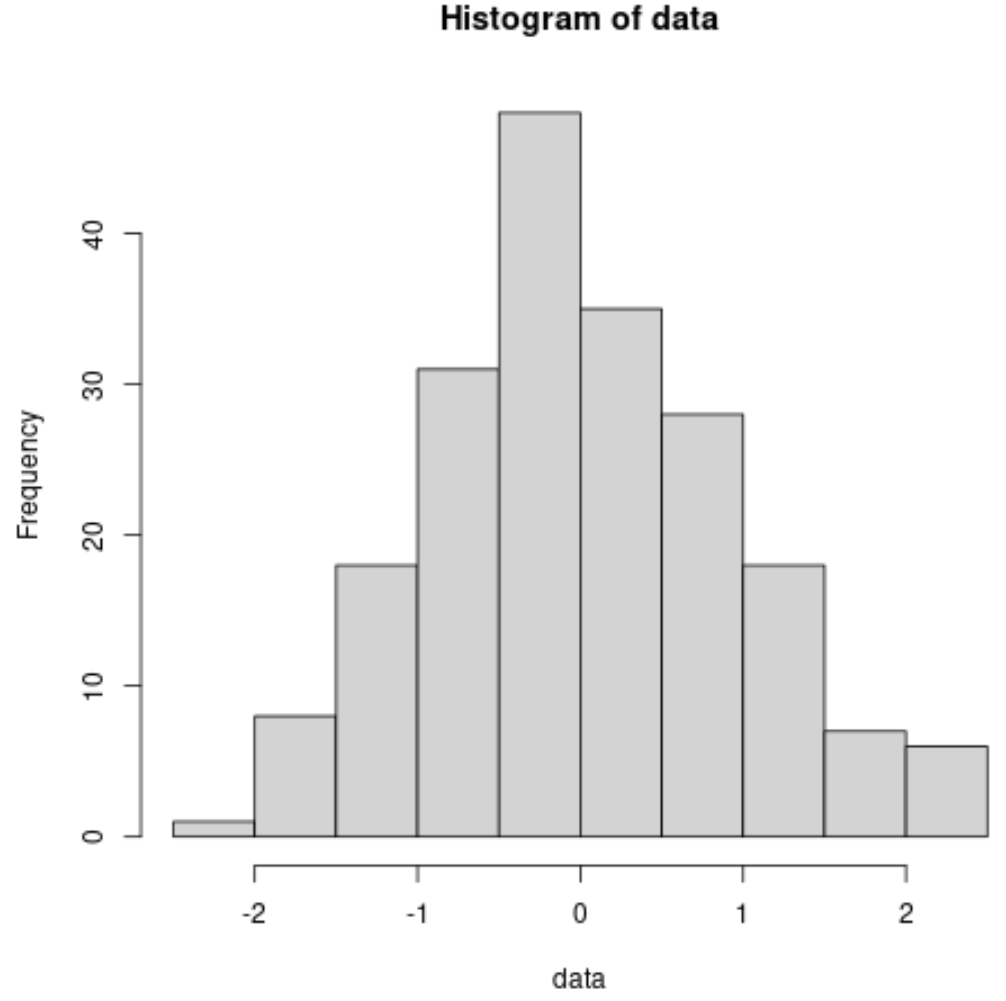
지수 사전 분포를 따르는 데이터세트에 대한 히스토그램을 만드는 방법은 다음과 같습니다.

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create a histogram to visualize the distribution
hist(data) 

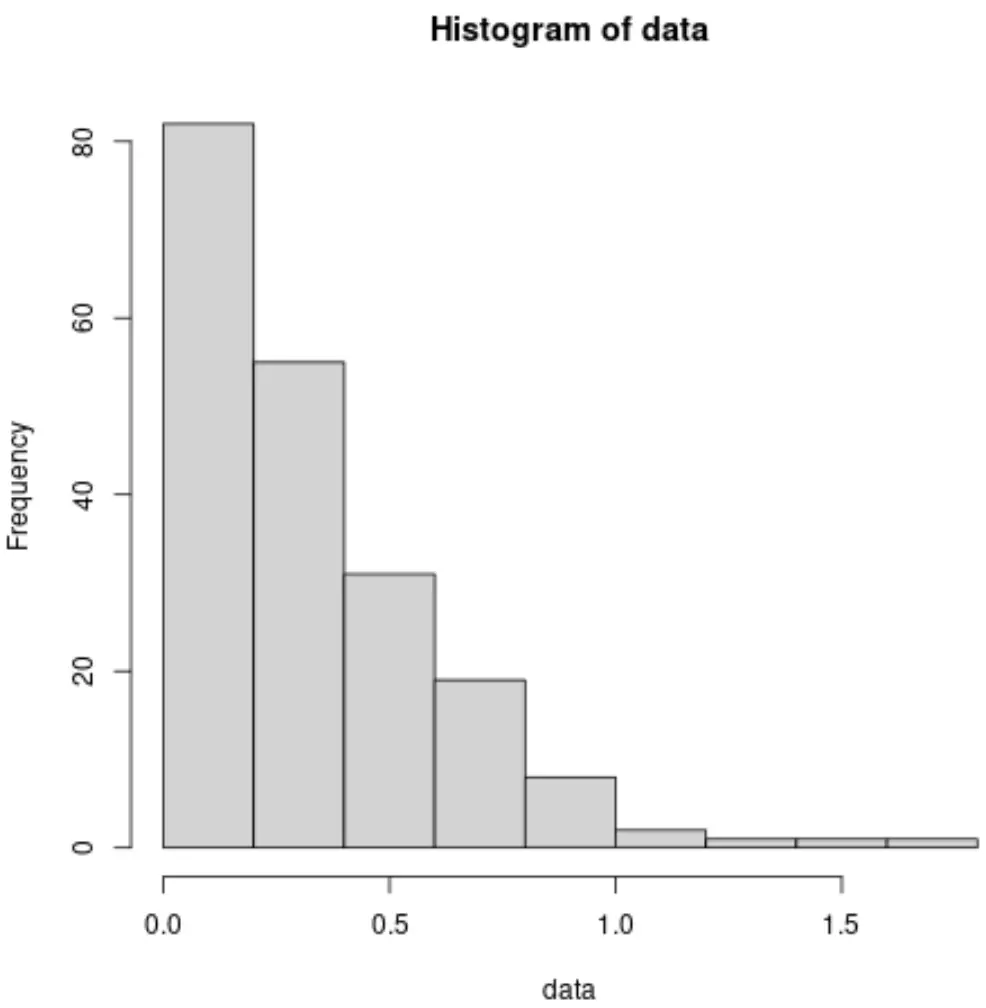
히스토그램이 전혀 종형 곡선처럼 보이지 않는 것을 볼 수 있는데, 이는 데이터가 정규 분포를 따르지 않는다는 것을 분명히 나타냅니다.

추가 리소스

통계에서 정규성 가정은 무엇입니까?
R에서 QQ 플롯을 만드는 방법
Excel에서 QQ 플롯을 만드는 방법
Python에서 QQ 플롯을 만드는 방법