회귀 기울기의 중요성을 테스트하는 방법

12개 주택의 면적과 가격을 보여주는 다음 데이터 세트가 있다고 가정해 보겠습니다.

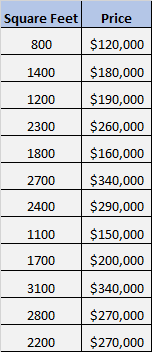
우리는 면적과 가격 사이에 중요한 관계가 있는지 알고 싶습니다.

데이터가 어떤 모양인지 알아보기 위해 먼저 x축에 평방피트 , y축에 가격이 있는 산점도를 만듭니다.

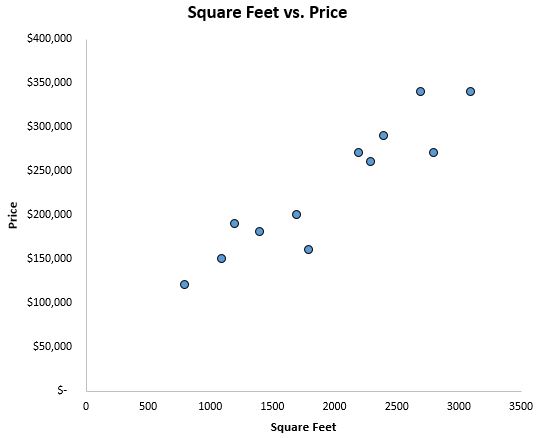
우리는 면적과 가격 사이에 양의 상관관계가 있음을 분명히 알 수 있습니다. 면적이 늘어나면 집값도 오르는 경향이 있다.

그러나 면적과 가격 사이에 통계적으로 유의미한 관계가 있는지 확인하려면 간단한 선형 회귀 분석을 실행해야 합니다.

따라서 우리는 평방 피트를 예측 변수로 사용하고 가격을 응답으로 사용하여 간단한 선형 회귀를 실행하고 다음 결과를 얻습니다.

Excel, SPSS, R 또는 기타 소프트웨어에서 단순 선형 회귀를 실행하면 위에 표시된 것과 유사한 결과를 얻을 수 있습니다.

간단한 선형 회귀는 가장 적합한 선, 즉 산점도의 데이터에 가장 잘 맞는 선의 방정식을 생성한다는 점을 기억하십시오. 이 최적 적합선은 다음과 같이 정의됩니다.

ŷ = _b0 + _b1x

여기서 ŷ는 반응 변수의 예측 값이고, b ₀ 은 절편이고, b ₁ 은 회귀 계수이고, x는 예측 변수의 값입니다.

b ₀ 값은 원점 계수인 47588.70으로 제공됩니다.

b ₁ 의 값은 예측 변수 Square Feet 의 계수 (93.57)로 제공됩니다.

따라서 이 예에서 가장 적합한 선은 ŷ = 47588.70+ 93.57x 입니다.

이 최적선을 해석하는 방법은 다음과 같습니다.

• b ₀ : 평방 피트 값이 0일 때 예상되는 평균 가격 값은 $47,588.70입니다. (이 경우 집의 평방 피트가 0이 될 수 없으므로 절편을 해석하는 것은 실제로 의미가 없습니다.)
• b ₁ : 평방피트가 추가될 때마다 예상되는 평균 가격 인상은 $93.57입니다.

따라서 이제 우리는 평방피트가 추가될 때마다 예상되는 평균 가격 상승 폭이 93.57달러라는 것을 알고 있습니다.

이러한 증가가 통계적으로 유의한지 확인하려면 B ₁ 에 대한 가설 검정을 수행하거나 B ₁ 에 대한 신뢰 구간을 구성해야 합니다.

참고 : 가설 검정과 신뢰 구간은 항상 동일한 결과를 제공합니다.

회귀 기울기에 대한 신뢰 구간 구축

회귀 기울기에 대한 신뢰 구간을 구성하려면 다음 공식을 사용합니다.

신뢰 구간 = b ₁ +/- (t _{1-∝/2, n-2} ) * (b ₁ 의 표준 오차)

금:

• b ₁ 은 회귀 결과에 제공된 기울기 계수입니다.
• (t _{1-∝/2, n-2} )는 자유도가 n-2인 1-∝ 신뢰 수준에 대한 임계 t 값입니다. 여기서 n 은 데이터 세트의 총 관측 수입니다.
• (b ₁ 의 표준오차)는 회귀분석 결과에 주어진 b ₁ 의 표준오차이다.

예를 들어 B ₁ 에 대한 95% 신뢰 구간을 구성하는 방법은 다음과 같습니다.

• b _{1 은} 회귀 출력에서 93.57입니다.
• 95% 신뢰 구간을 사용하므로 ∝ = 0.05, n-2 = 12-2 = 10이므로 t 분포표에 따르면 t _{0.975, 10} 은 2.228입니다.
• ( _b1 의 표준 오차)는 회귀 출력에서 11.45입니다.

따라서 B ₁ 에 대한 95% 신뢰 구간은 다음과 같습니다.

93.57 +/- (2.228) * (11.45) = (68.06, 119.08)

이는 추가 평방 피트당 실제 평균 가격 인상이 $68.06에서 $119.08 사이라고 95% 확신한다는 의미입니다.

$0는 이 구간에 포함되지 않으므로 면적과 가격 간의 관계는 95% 신뢰 수준에서 통계적으로 유의합니다.

회귀 기울기에 대한 가설 검정 수행

회귀 기울기에 대한 가설 검정을 수행하기 위해 모든 가설 검정에 대한 5가지 표준 단계를 따릅니다.

1단계. 가설을 진술합니다.

귀무가설(H0): B ₁ = 0

대립 가설: (Ha): B ₁ ≠ 0

2단계. 사용할 유의 수준을 결정합니다.

이전 예에서 95% 신뢰 구간을 구성했으므로 여기서는 동등한 접근 방식을 사용하고 유의 수준 0.05를 사용하도록 선택합니다.

3단계. 검정 통계량과 해당 p-값을 찾습니다.

이 경우 검정 통계량은 t = b 계수 ₁ / _b 표준 오차(n-2 자유도 포함)입니다. 회귀 결과에서 다음 값을 찾을 수 있습니다.

따라서 검정 통계량 t = 92.89 / 13.88 = 6.69입니다.

자유도 10 및 양측 테스트에서 점수 6.69 의 T 점수 대 P 값 계산기를 사용하면 p 값은 0.000 입니다.

4단계. 귀무가설을 기각하거나 기각하지 않습니다.

p-값이 유의 수준인 0.05보다 낮으므로 귀무 가설을 기각합니다.

5단계. 결과를 해석합니다.

귀무가설을 기각했기 때문에 평방피트가 추가될 때마다 실제 평균 가격 상승이 0이 아니라고 말할 수 있는 충분한 증거가 있습니다.