Excel에서 가중 이동 평균을 찾는 방법

가중 이동 평균은 시계열 데이터를 평활화하여 데이터의 “노이즈”를 줄이고 패턴과 추세를 보다 쉽게 식별하는 데 사용할 수 있는 기술입니다.

가중 이동 평균의 기본 개념은 이전 기간의 평균을 취하여 특정 기간의 “평균” 값에 도달하고 최근 기간에 더 많은 가중치를 부여하는 것입니다.

이 튜토리얼에서는 Excel에서 시계열 데이터에 대한 가중 이동 평균을 찾는 방법을 보여줍니다.

예: Excel의 가중 이동 평균

10개 기간에 걸쳐 특정 회사의 매출을 보여주는 다음 데이터 세트가 있다고 가정해 보겠습니다.

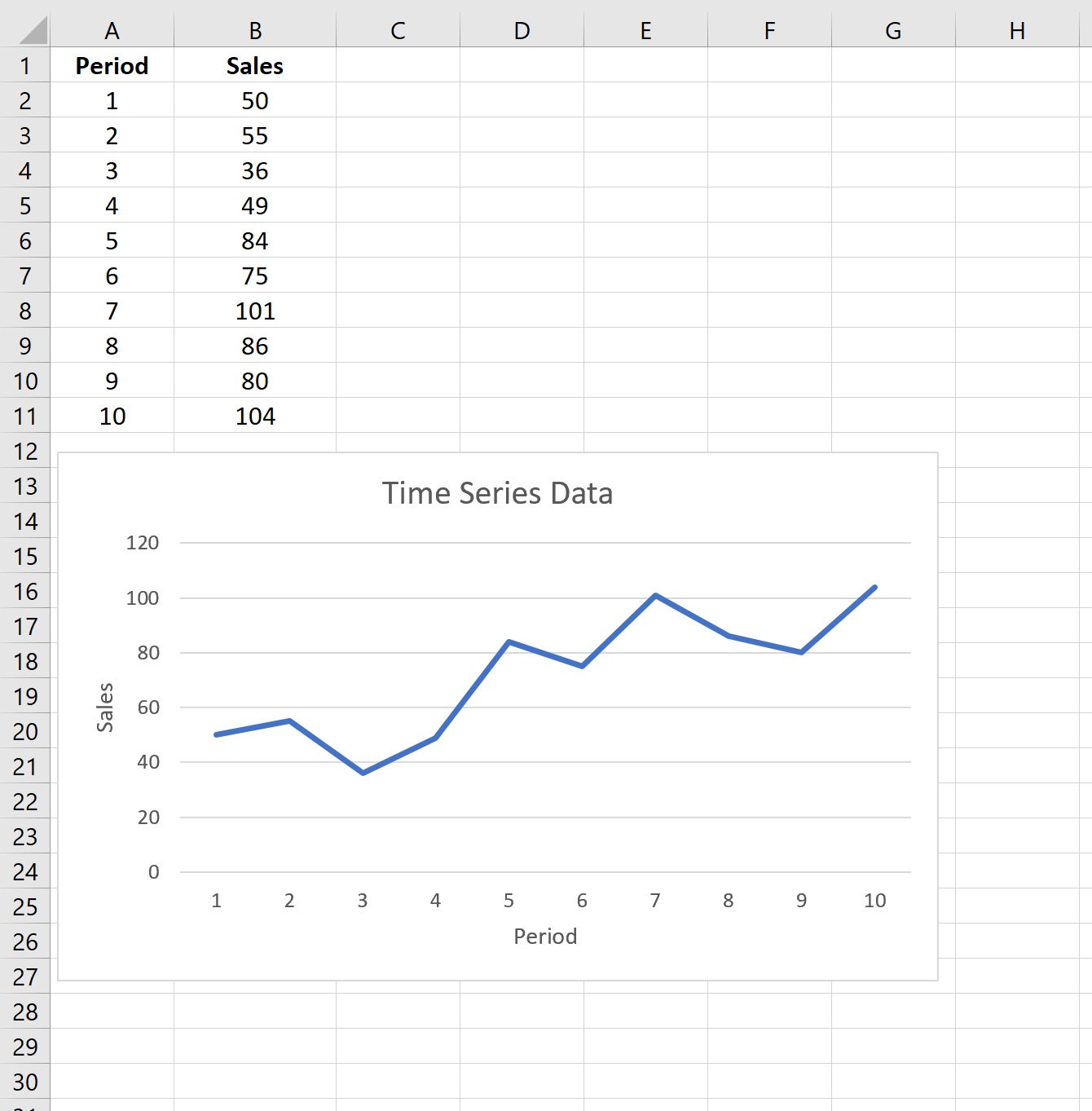
이 기간의 가중 이동 평균을 계산하려면 다음 단계를 수행할 수 있습니다.

1단계: 가중 이동 평균 계산에 포함할 이전 기간 수를 결정합니다.

이 예에서는 세 개의 마침표를 사용합니다.

2단계: 각 기간에 할당할 가중치를 결정합니다.

다음과 같이 가중치를 할당하겠습니다.

• 현재 기간 동안 0.5
• 이전 기간의 경우 0.3
• 이전 두 기간 동안 0.2

총 가중치의 합은 1과 같아야 합니다.

3단계: 각 기간의 가중 이동 평균을 계산합니다.

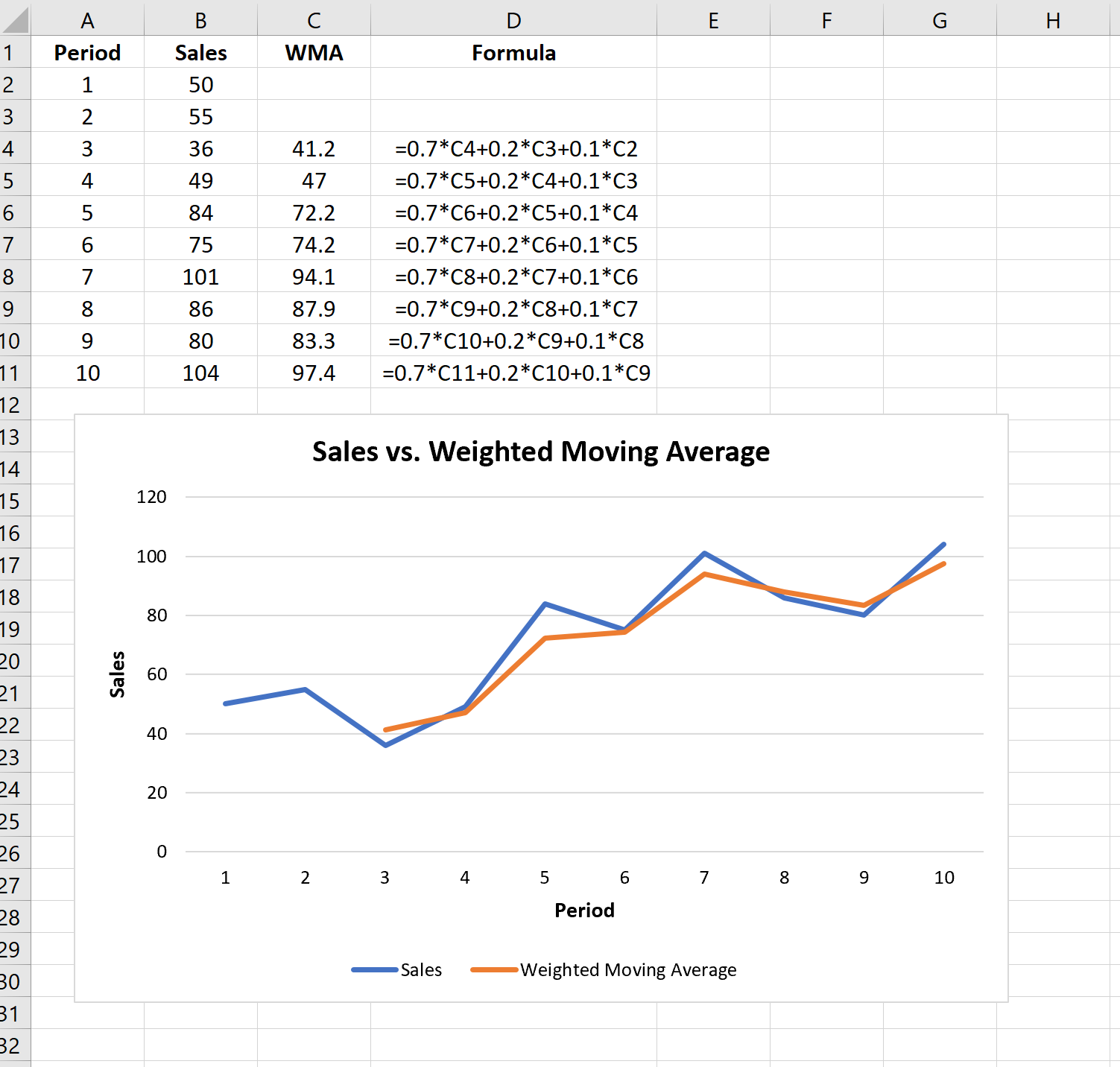
아래 이미지에서 C열은 기간 3의 WMA(가중 이동 평균)를 보여주고 D열은 이를 계산하는 데 사용한 공식을 보여줍니다.

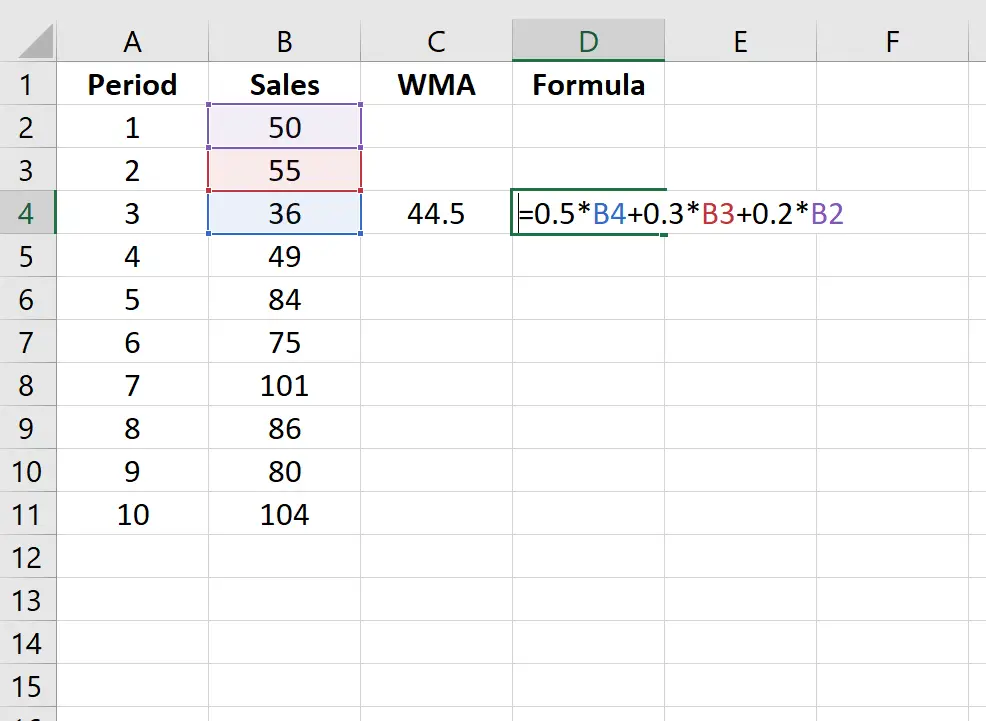
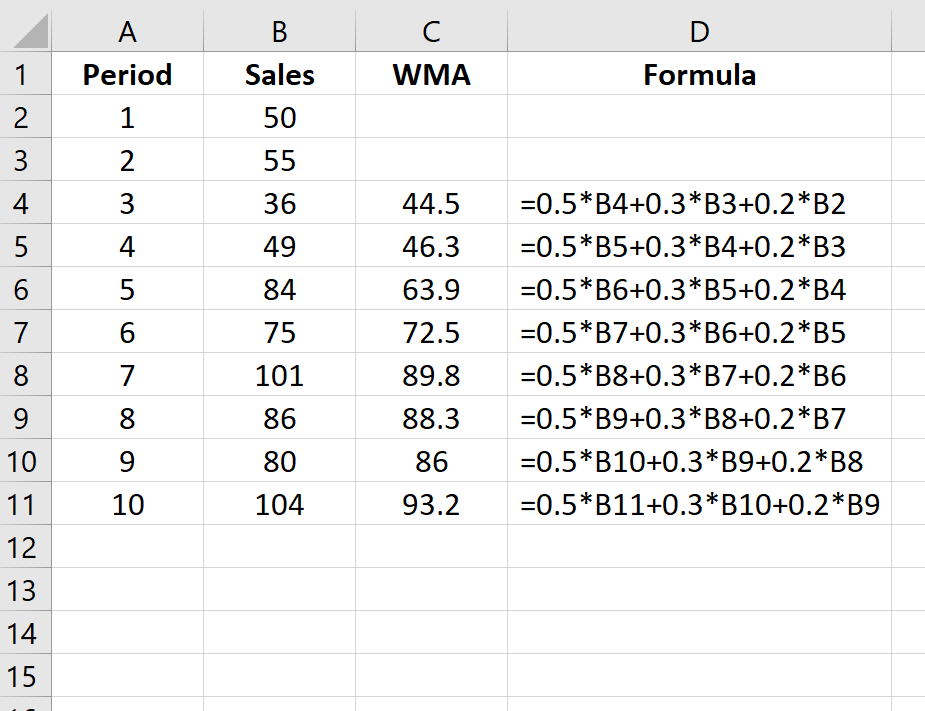
비슷한 공식을 사용하여 각 기간의 가중 이동 평균을 찾을 수 있습니다.

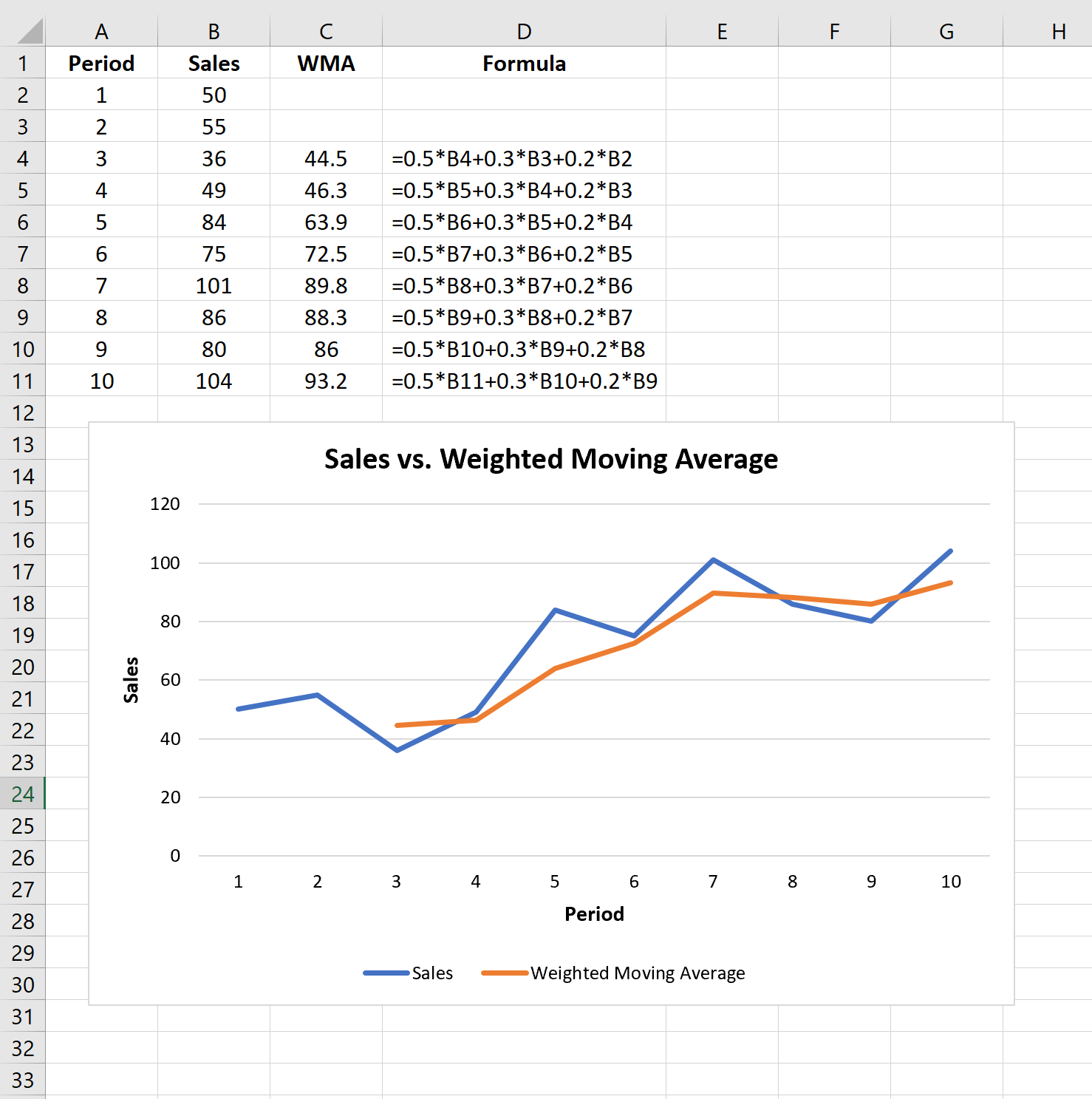
실제 매출과 가중 이동 평균을 시각화하기 위해 선형 차트를 생성하면 WMA 선이 최고점과 최저점이 적어 더 매끄러워진다는 것을 알 수 있습니다. 이것이 가중 이동 평균의 기본 아이디어입니다. 이를 통해 추가 노이즈 없이 데이터의 실제 기본 추세를 볼 수 있습니다.

가중 이동 평균을 조정합니다.

조정하여 가중 이동 평균을 다르게 계산할 수 있는 두 가지 숫자가 있습니다.

사용된 이전 기간의 수입니다 . 이 예에서는 가중 이동 평균을 계산하기 위해 이전 세 기간을 사용했지만 4, 5, 6 등을 선택할 수도 있었습니다. 일반적으로 계산에 사용하는 기간이 많을수록 가중 이동 평균선이 더 부드러워집니다. 될거야.

각 기간에 할당된 가중치입니다 . 이 예에서는 가중치 0.5, 0.3, 0.2를 할당했지만 합계가 1인 한 어떤 가중치 조합도 선택할 수 있습니다. 일반적으로 가장 최근 기간에 가중치를 더 많이 할당할수록 더 매끄러워집니다. 가중 이동 평균선은 다음과 같습니다.

이를 설명하기 위해 WMA 계산에 세 기간을 다시 사용하고 대신 다음 가중치를 사용하는 경우를 생각해 보십시오.

• 현재 기간 동안 0.7
• 이전 기간의 경우 0.2
• 이전 두 기간 동안 0.1

현재 기간에 많은 가중치를 두었기 때문에 가중 이동 평균선은 덜 유동적이며 실제 매도선과 더 유사합니다.

단순 이동 평균 및 가중 이동 평균

단순이동평균은 계산에 사용된 모든 기간에 동일한 가중치를 부여하여 이동평균을 계산하는 방법입니다.

예를 들어 3개의 기간을 사용하여 이동 평균을 계산하는 경우 각 기간에 할당되는 가중치는 0.333이 됩니다. 또는 4개의 기간을 사용하여 이동 평균을 계산하는 경우 각 기간에 할당되는 가중치는 0.25가 됩니다.

단순 이동 평균은 계산하기가 더 간단하지만 가중 이동 평균을 사용하면 최근 기간에 더 높은 가중치를 할당할 수 있다는 장점이 있습니다. 이는 데이터가 특정 방향으로 움직이고 추세를 보다 명확하게 파악하려는 경우에 유용합니다.

예를 들어, 시즌 내내 실력이 향상되는 농구 선수가 득점한 점수의 가중 이동 평균을 계산한다고 가정해 보겠습니다.

5경기 이동 평균을 사용하면 가장 최근 경기에서 득점한 점수에 더 많은 가중치를 부여하여 득점해야 하는 점수에 대한 더 명확한 아이디어를 얻을 수 있습니다.

추가 리소스

다음 자습서에서는 Excel에서 다른 일반적인 측정항목을 계산하는 방법을 설명합니다.

Excel에서 지수 이동 평균을 계산하는 방법
Excel에서 누적 평균을 계산하는 방법