Stata의 회귀 분석에서 강력한 표준 오류를 사용하는 방법

다중 선형 회귀는 여러 설명 변수와 응답 변수 간의 관계를 이해하는 데 사용할 수 있는 방법입니다.

불행하게도 회귀 분석에서 자주 발생하는 문제는 이분산성(heteroscedasticity) 으로 알려져 있으며, 측정된 값의 범위에 걸쳐 잔차의 분산이 체계적으로 변화하는 경우입니다.

이로 인해 회귀 계수 추정치의 분산이 증가하지만 회귀 모델에서는 이를 고려하지 않습니다. 이로 인해 회귀 모델에서는 실제로는 그렇지 않은데도 모델의 항이 통계적으로 유의하다고 주장할 가능성이 훨씬 더 높아집니다.

이 문제를 설명하는 한 가지 방법은 이분산성 문제에 대해 보다 “견고하고” 회귀 계수의 실제 표준 오차에 대한 보다 정확한 측정값을 제공하는 경향이 있는 견고한 표준 오차 를 사용하는 것입니다.

이 튜토리얼에서는 Stata의 회귀 분석에서 강력한 표준 오류를 사용하는 방법을 설명합니다.

예: Stata의 강력한 표준 오류

회귀 분석에서 강력한 표준 오류를 사용하는 방법을 설명하기 위해 자동으로 통합된 Stata 데이터 세트를 사용할 것입니다.

1단계: 데이터를 로드하고 표시합니다.

먼저 다음 명령을 사용하여 데이터를 로드합니다.

시스템 자동 사용

그런 다음 다음 명령을 사용하여 원시 데이터를 표시합니다.

br

2단계: 강력한 표준 오류 없이 다중 선형 회귀를 수행합니다.

다음으로, 가격을 응답 변수로, mpg 와 무게를 설명 변수로 사용하여 다중 선형 회귀를 수행하기 위해 다음 명령을 입력합니다.

회귀 가격 mpg 무게

3단계: 강력한 표준 오류를 사용하여 다중 선형 회귀를 수행합니다.

이제 우리는 정확히 동일한 다중 선형 회귀를 수행할 것이지만 이번에는 Stata가 강력한 표준 오류를 사용하는 방법을 알 수 있도록 vce(robust) 명령을 사용할 것입니다:

회귀 가격 mpg 무게, vce(강건함)

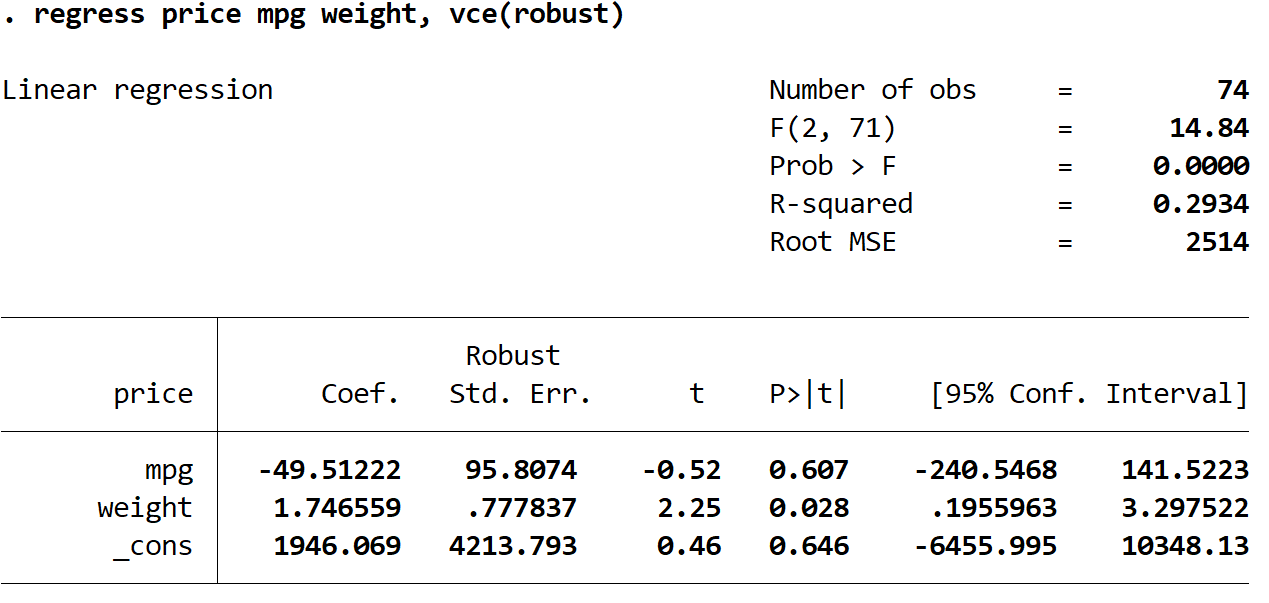
여기서 주목해야 할 몇 가지 흥미로운 사항이 있습니다.

1. 계수 추정치는 동일하게 유지되었습니다 . 강력한 표준 오류를 사용하면 계수 추정치가 전혀 변경되지 않습니다. mpg, 무게 및 상수에 대한 계수 추정치는 두 회귀 분석 모두에 대해 다음과 같습니다.

• mpg: -49.51222
• 무게: 1.746559
• _반대: 1946.069

2. 표준오차가 변경되었습니다 . 로버스트 표준 오류를 사용하면 각 계수 추정값에 대한 표준 오류가 증가합니다.

참고: 대부분의 경우 로버스트 표준 오류는 일반 표준 오류보다 크지만, 드물게 로버스트 표준 오류가 실제로 더 작을 수도 있습니다.

3. 각 계수의 검정통계량이 변경되었습니다. 각 검정 통계량 t 의 절대값이 감소했습니다. 실제로 검정 통계량은 추정 계수를 표준 오차로 나누어 계산됩니다. 따라서 표준 오차가 클수록 검정 통계량의 절대값은 작아집니다.

4. p-값이 변경되었습니다 . 각 변수의 p-값도 증가했다는 점에 유의하세요. 이는 검정 통계량이 작을수록 p-값이 커지기 때문입니다.

계수에 대한 p 값이 변경되었지만 mpg 변수는 α = 0.05에서 여전히 통계적으로 유의하지 않으며 변수 가중치는 α = 0.05에서 여전히 통계적으로 유의합니다.