2-표본 t-검정: 정의, 공식 및 예

2-표본 t-검정은 두 모집단의 평균이 같은지 여부를 확인하는 데 사용됩니다.

이 튜토리얼에서는 다음 내용을 설명합니다.

• 2-표본 t-검정을 수행하는 동기.
• 2-표본 t-검정을 수행하기 위한 공식입니다.
• 2-표본 t-검정을 수행하기 위해 충족되어야 하는 가정입니다.
• 2-표본 t-검정을 수행하는 방법의 예입니다.

2-표본 t-검정: 동기

서로 다른 두 종의 거북이의 평균 무게가 같은지 여부를 알고 싶다고 가정해 보겠습니다. 각 개체군에는 수천 마리의 거북이가 있기 때문에 각 거북이를 개별적으로 돌아다니며 무게를 측정하는 것은 너무 많은 시간과 비용이 소요됩니다.

대신, 각 모집단에서 거북이 15마리의 간단한 무작위 표본을 추출하고 각 표본의 평균 체중을 사용하여 두 모집단의 평균 체중이 같은지 확인할 수 있습니다.

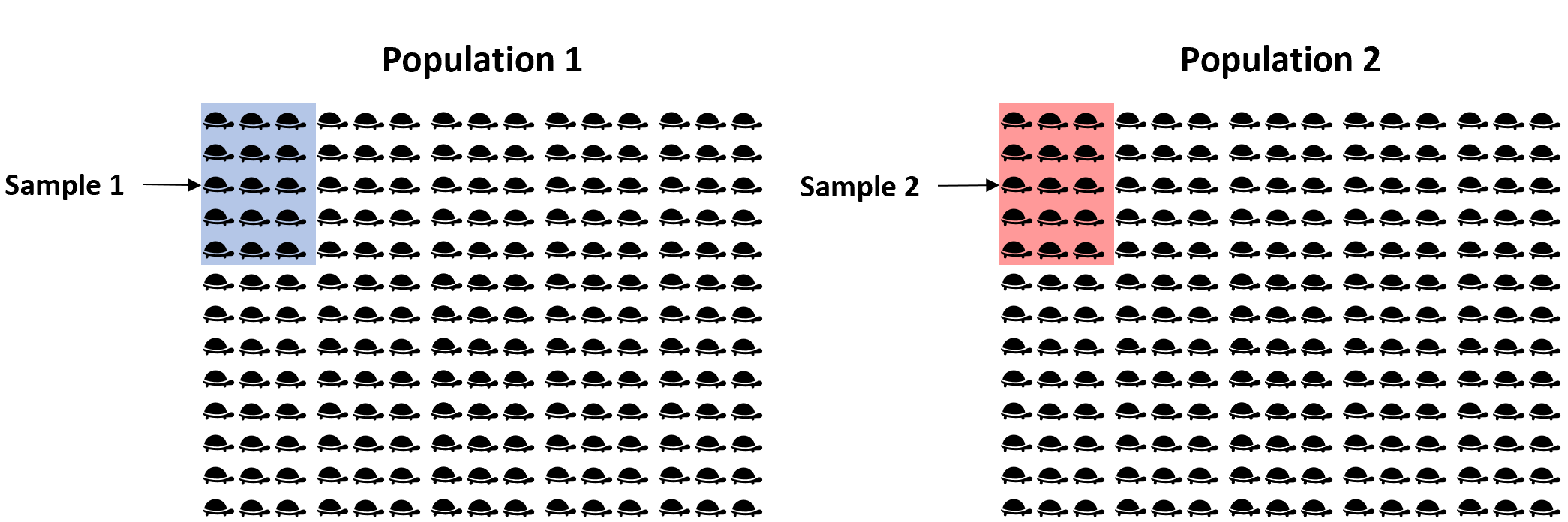
그러나 두 샘플 간의 평균 중량이 최소한 약간씩 다를 것이라는 것은 사실상 보장됩니다. 문제는 이 차이가 통계적으로 유의한지 여부입니다 . 다행히도 2-표본 t-검정을 통해 이 질문에 답할 수 있습니다.

2-표본 t-검정: 공식

2-표본 t-검정은 항상 다음과 같은 귀무 가설을 사용합니다.

• H ₀ : μ ₁ = μ ₂ (두 모집단 평균이 동일함)

대립 가설은 양측, 왼쪽 또는 오른쪽일 수 있습니다.

• H ₁ (양측): μ ₁ ≠ μ ₂ (두 모집단의 평균이 동일하지 않음)
• H ₁ (왼쪽): μ ₁ < μ ₂ (모집단 1의 평균이 모집단 2의 평균보다 낮음)
• H ₁ (오른쪽): μ ₁ > μ ₂ (모집단 1의 평균이 모집단 2의 평균보다 큽니다)

t-검정 통계를 계산하기 위해 다음 공식을 사용합니다.

검정 통계량: ( x ₁ – x ₂ ) / s _p (√ 1/n ₁ + 1/n ₂ )

여기서 x ₁ 과 x ₂ 는 표본 평균이고, n ₁ 과 n ₂ 는 표본 크기이며, s _p는 다음과 같이 계산됩니다.

s _p = √ (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² / (n ₁ +n ₂ -2)

여기서 s ₁ ² 및 s ₂ ² 는 표본 분산입니다.

자유도가 (n ₁ + n ₂ -1)인 t-검정 통계량에 해당하는 p-값이 선택한 유의 수준(일반적인 선택은 0.10, 0.05 및 0, 01)보다 작은 경우 귀무가설을 기각할 수 있다. .

2-표본 t-검정: 가설

2-표본 t-검정의 결과가 유효하려면 다음 가정이 충족되어야 합니다.

• 한 표본의 관측치는 다른 표본의 관측치와 독립적이어야 합니다.
• 데이터는 대략적으로 정규 분포를 따라야 합니다.
• 두 표본의 분산은 대략 동일해야 합니다. 이 가정이 충족되지 않으면 대신 Welch의 t-검정을 수행해야 합니다.
• 두 샘플의 데이터는 무작위 샘플링 방법을 사용하여 얻은 것입니다.

2-표본 t-검정 : 예

서로 다른 두 종의 거북이의 평균 무게가 같은지 여부를 알고 싶다고 가정해 보겠습니다. 이를 테스트하기 위해 다음 단계를 사용하여 α = 0.05 유의 수준에서 2-샘플 t-테스트를 수행합니다.

1단계: 샘플 데이터를 수집합니다.

다음 정보를 사용하여 각 개체군에서 무작위로 거북이 표본을 수집한다고 가정합니다.

샘플 1:

• 표본 크기 n ₁ = 40
• 평균 샘플 중량 x ₁ = 300
• 표본 표준 편차 s ₁ = 18.5

샘플 2:

• 표본 크기 n ₂ = 38
• 평균 샘플 중량 x ₂ = 305
• 표본 표준 편차 s ₂ = 16.7

2단계: 가정을 정의합니다.

다음 가정을 사용하여 2-표본 t-검정을 수행합니다.

• H ₀ : μ ₁ = μ ₂ (두 모집단 평균이 동일함)
• H ₁ : μ ₁ ≠ μ ₂ (두 모집단 평균이 동일하지 않음)

3단계: t -검정 통계량을 계산합니다.

먼저 합동 표준편차 s _{p 를} 계산합니다.

s _p = √ (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² / (n ₁ +n ₂ -2) = √ ( 40-1)18.5 ² + (38-1) 16.7 ² / (40+38-2) = 17.647

다음으로 t -test 통계량을 계산합니다.

t = ( x ₁ – x ₂ ) / s _p (√ 1/n ₁ + 1/n ₂ ) = (300-305) / 17.647(√ 1/40 + 1/38 ) = -1.2508

4단계: t- 검정 통계량의 p-값을 계산합니다.

T Score to P Value Calculator 에 따르면 t = -1.2508 및 자유도 = n ₁ + n ₂ -2 = 40+38-2 = 76과 연관된 p-값은 0.21484 입니다.

5단계: 결론을 도출합니다.

이 p-값은 유의 수준 α = 0.05보다 낮지 않으므로 귀무 가설을 기각할 수 없습니다. 이 두 개체군 사이의 거북이 평균 체중이 다르다고 말할 수 있는 충분한 증거가 없습니다.

참고: 2-표본 t- 검정 계산기를 사용하여 전체 2-표본 t-검정 을 수행할 수도 있습니다.

추가 리소스

다음 자습서에서는 다양한 통계 프로그램을 사용하여 2-표본 t-검정을 수행하는 방법을 설명합니다.

Excel에서 2-표본 t-검정을 수행하는 방법
SPSS에서 2-표본 t-검정을 수행하는 방법
Stata에서 2-표본 t-검정을 수행하는 방법
R에서 2-표본 t-검정을 수행하는 방법
Python에서 2-표본 t-검정을 수행하는 방법
TI-84 계산기에서 2-표본 t-검정을 수행하는 방법