몬티홀 문제: 간단한 시각적 설명
Let’s Make a Deal 이라는 오래된 게임 쇼에서 진행자 Monty Hall은 참가자들에게 세 개의 문을 제시했습니다.
문 중 하나에는 상품이 들어 있었지만 나머지 두 개에는 상품이 들어 있지 않았습니다.
Monty는 참가자에게 어느 문에 상품이 들어 있다고 생각하는지 선택하도록 요청했습니다.
참가자가 문을 선택하면 Monty는 상품이 들어 있지 않은 문을 열었습니다.
상품은 닫힌 두 문 중 하나에 남아있었습니다.
그런 다음 Monty는 후보자에게 문을 바꾸고 싶은지 물었습니다.
믿기 어려울 수도 있지만, 게임의 이 시점에서 문을 바꾸면 실제로 승리할 확률이 더 높아진다는 것이 밝혀졌습니다.
이유를 알아보려면 계속 읽어보세요!
몬티 홀 문제를 시각적으로 설명
문을 바꾸면 승리할 확률이 더 높아지는 이유를 설명하기 위해 문 1을 먼저 선택하는 다음 시나리오를 고려해 보세요.
시나리오 1: 당신이 문 1을 선택했고 상품은 실제로 문 1 뒤에 있습니다.
이 경우 몬티는 2번이나 3번 문을 열고 양쪽 문 뒤에는 아무것도 없다는 것을 보여줄 것입니다. 1번 문에 머무르면 승리합니다 .
시나리오 2: 당신이 문 1을 선택했고 상품은 실제로 문 2 뒤에 있습니다.
이 경우 몬티는 3번 문을 열고 그 뒤에 아무것도 없다는 것을 보여줘야 합니다. 1번 문에 머무르면 패배합니다 .
시나리오 3: 당신이 문 1을 선택했고 상품은 실제로 문 3 뒤에 있습니다.
이 경우 몬티는 2번 문을 열고 그 뒤에 아무것도 없다는 것을 보여줘야 합니다. 1번 문에 머무르면 패배합니다 .
이것은 모두 1번 문을 선택한 경우에 가능한 결과입니다. 1번 문에 머무르면 시간이 3분의 1만 절약된다는 점에 유의하세요. 하지만 변경하면 시간이 3분의 2 절약됩니다.
다음 표에는 이 게임 쇼에서 가능한 모든 시나리오와 유지 관리 및 변경과 관련된 결과가 요약되어 있습니다.
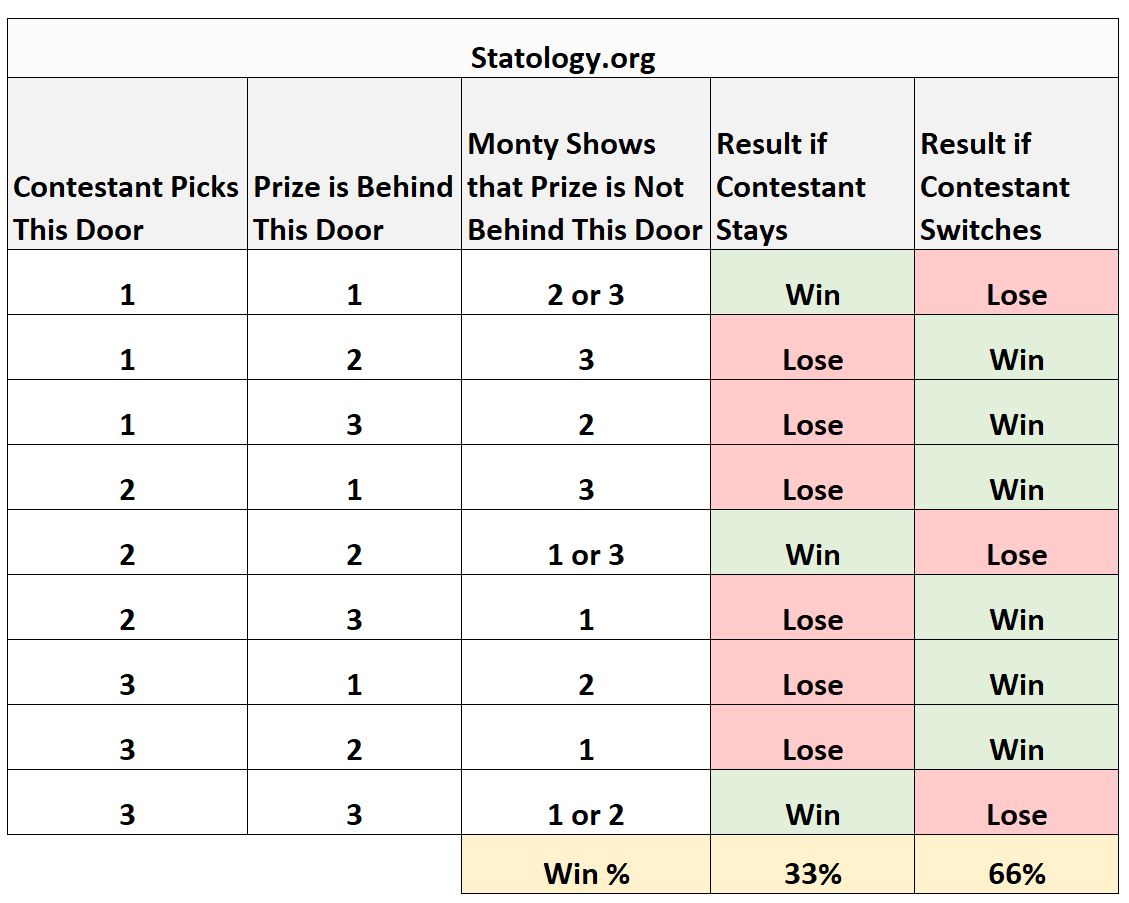
표를 보면 머무를 때는 33% 의 확률로 승리하지만 전환할 때는 66% 의 확률로 승리한다는 것을 알 수 있습니다.
따라서 문을 바꾸면 상을 받을 확률이 높아집니다.
이것이 직관적으로 이해되지 않는 것처럼 보일 수도 있지만 수학은 거짓말을 하지 않습니다.