T 테스트에서 p 값을 수동으로 계산하는 방법

통계에서 가장 일반적으로 사용되는 테스트 중 하나는 모집단의 평균이 특정 값과 같은지 여부를 확인하는 데 자주 사용되는 t-테스트 입니다.

예를 들어, 특정 식물 종의 평균 높이가 15인치인지 알고 싶다고 가정해 보겠습니다. 이를 테스트하기 위해 20개 식물의 무작위 표본을 수집하고 표본 평균과 표본 표준 편차를 찾은 다음 t-검정을 수행하여 평균 높이가 실제로 15인치인지 확인할 수 있습니다.

검정의 귀무가설과 대립가설은 다음과 같습니다.

H ₀ : µ = 15

H _a : µ ≠ 15

검정 통계량의 공식은 다음과 같습니다.

t = ( X -μ) / (s/ √n )

여기서 x 는 표본 평균, μ 는 가상 평균(이 예에서는 15), s 는 표본 표준 편차, n 은 표본 크기입니다.

t 값을 알고 나면 통계 소프트웨어나 온라인 계산기를 사용하여 해당 p-값을 찾을 수 있습니다. p-값이 특정 알파 수준(일반적으로 0.01, 0.05, 0.10)보다 낮으면 귀무 가설을 기각하고 평균 식물 높이가 15인치에서 동일 하지 않다는 결론을 내릴 수 있습니다.

그러나 t-분포표를 사용하여 검정 p-값을 수동으로 추정하는 것도 가능합니다 . 이 기사에서는 이를 수행하는 방법을 설명합니다.

예: t-검정에서 p-값 수동 계산

문제 : Bob은 특정 식물 종의 평균 높이가 15인치인지 알고 싶어합니다. 이를 테스트하기 위해 그는 20개 식물의 무작위 표본을 수집하고 표본 평균이 14인치이고 표본 표준 편차가 3인치임을 확인했습니다. 실제 평균 인구 키가 실제로 15인치인지 확인하려면 알파 수준 0.05를 사용하여 t-테스트를 수행합니다.

해결책:

1단계: 귀무가설과 대립가설을 진술합니다.

H ₀ : µ = 15

H _a : µ ≠ 15

2단계: 검정 통계량을 찾습니다.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1.49

3단계: 검정 통계량에 대한 p-값을 찾습니다.

p-값을 수동으로 찾으려면 자유도가 n-1인 t-분포표를 사용해야 합니다. 이 예에서 표본 크기는 n = 20이므로 n-1 = 19입니다.

아래 t-분포표에서 왼쪽의 “19”에 해당하는 행을 보고 테스트 통계량 1.49 의 절대값을 찾아야 합니다.

1.49는 표에 나타나지 않지만 1.328 과 1.729 두 값 사이에 속합니다.

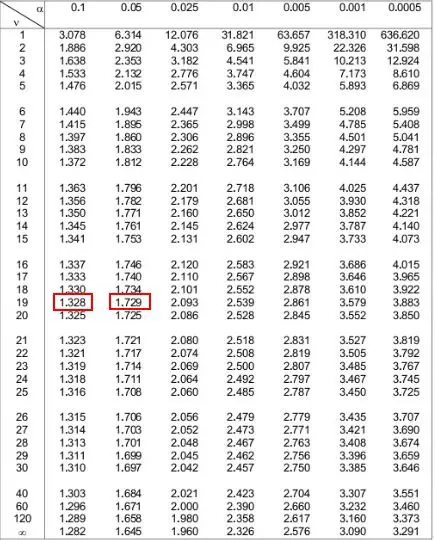
그런 다음 이 두 숫자에 해당하는 표 상단의 두 알파 수준을 볼 수 있습니다. 0.1 과 0.05 인 것을 알 수 있습니다.

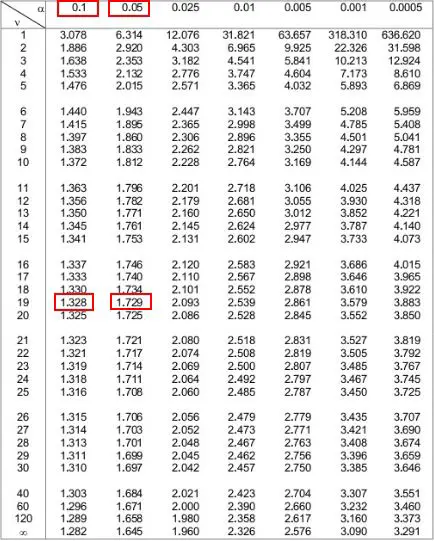
이는 단측 검정의 p-값이 0.1에서 0.05 사이에 있음을 의미합니다. .075라고 부르자. 우리의 t-검정은 양측 검정이므로 이 값에 2를 곱해야 합니다. 따라서 추정된 p-값은 0.075 * 2 = 0.15 입니다.

4단계: 결론을 도출합니다.

이 p-값은 선택한 알파 수준인 0.05보다 낮지 않기 때문에 귀무 가설을 기각할 수 없습니다. 따라서 우리는 이 식물 종의 실제 평균 높이가 15인치가 아니라고 말할 수 있는 충분한 증거가 없습니다.

계산기로 결과를 확인해보세요

t- 검정 통계와 자유도를 온라인 p-값 계산기 에 연결하여 추정된 p-값이 실제 p-값에 얼마나 가까운지 확인할 수 있습니다.

실제 p-값은 0.15264 이며, 이는 추정된 p-값 0.15 에 매우 가깝습니다.

결론

우리는 이 기사에서 t-분포표를 사용하여 t-검정의 p-값을 수동으로 추정하는 것이 가능하다는 것을 확인했습니다. 그러나 대부분의 시나리오에서는 p-값을 직접 계산할 필요가 없으며 R 및 Excel과 같은 통계 소프트웨어나 온라인 계산기를 사용하여 테스트의 정확한 p-값을 찾을 수 있습니다.

대부분의 경우, 특히 엄격한 통계 연구 및 실험에서는 계산기를 사용하여 t-검정에서 정확한 p-값을 최대한 정확하게 찾고 싶지만 항상 수동으로 추정할 수 있다는 것을 아는 것이 좋습니다. 꼭 필요한 경우 t-검정의 p-값을 사용하세요.