Stata에서 fisher의 정확한 테스트를 수행하는 방법
Fisher의 정확 검정은 두 범주형 변수 사이에 유의미한 연관성이 있는지 여부를 확인하는 데 사용됩니다. 일반적으로 2×2 테이블에서 하나 이상의 셀 개수가 5보다 작은 경우 카이제곱 독립성 검정 의 대안으로 사용됩니다.
이 튜토리얼에서는 Stata에서 Fisher의 정확한 테스트를 수행하는 방법을 설명합니다.
예: Stata의 Fisher 정확 검정
성별이 특정 대학의 정당 선호와 연관되어 있는지 여부를 알고 싶다고 가정해 보겠습니다. 이를 탐구하기 위해 우리는 캠퍼스 내 25명의 학생을 무작위로 설문조사했습니다. 성별에 따른 민주당 또는 공화당 학생 수는 아래 표에 나와 있습니다.
| 민주당 | 공화주의자 | |
|---|---|---|
| 남성 | 4 | 9 |
| 여성 | 8 | 4 |
성별과 정당 선호도 사이에 통계적으로 유의미한 연관성이 있는지 확인하기 위해 Fisher의 정확 검정을 수행할 수 있습니다.
Stata에서는 tabi 명령을 사용하여 Fisher의 Exact 테스트를 수행할 수 있습니다. 2×2 테이블의 상단 행과 하단 행을 구분하기 위해 \를 사용하여 왼쪽에서 오른쪽으로 개수를 입력합니다.
버선 4 9 \ 8 4
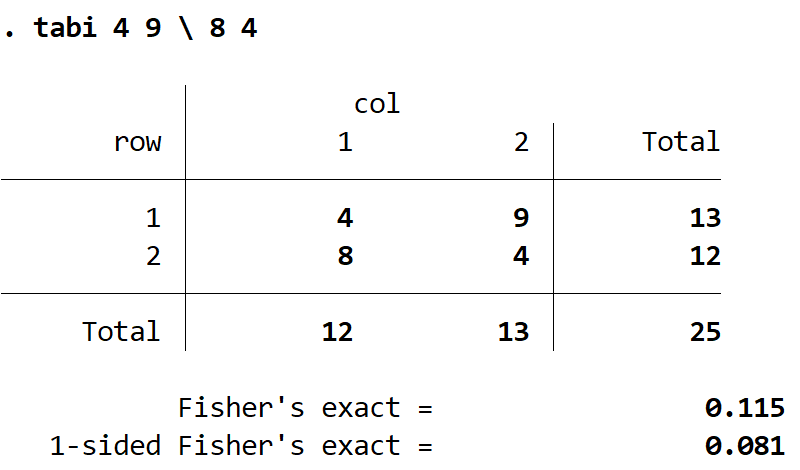
결과를 해석하는 방법은 다음과 같습니다.
출력 테이블: 이 테이블에는 입력한 각 셀의 개수가 표시됩니다.
Fisher의 정확 검정: 양측 Fisher의 정확 검정과 연관된 p-값입니다. 이 경우에는 0.115입니다.
단측 Fisher의 정확 검정: 단측 Fisher의 정확 검정과 관련된 p-값입니다. 이 경우에는 0.081입니다.
Fisher의 정확 검정의 귀무 가설은 두 변수가 독립적이라는 것입니다. 이 경우 귀무 가설은 성별과 정당 선호도가 독립적이라는 것입니다. 이는 양측 검정이므로 첫 번째 p-값인 0.115를 사용합니다.
이 p-값은 0.05 이상이므로 귀무가설을 기각하지 않습니다. 따라서 성별과 정당 선호도 사이에 유의미한 연관성이 있다고 말할 수 있는 충분한 증거가 없습니다.