Excel에서 fisher의 정확한 테스트를 수행하는 방법

Fisher의 정확 검정은 두 범주형 변수 사이에 유의미한 연관성이 있는지 여부를 확인하는 데 사용됩니다. 일반적으로 2×2 테이블에서 하나 이상의 셀 개수가 5보다 작은 경우 카이제곱 독립성 검정의 대안으로 사용됩니다.

이 튜토리얼에서는 Excel에서 Fisher의 정확한 테스트를 수행하는 방법을 설명합니다.

예: Excel에서 Fisher의 정확 검정

성별이 특정 대학의 정당 선호와 연관되어 있는지 여부를 알고 싶다고 가정해 보겠습니다. 이를 탐구하기 위해 우리는 캠퍼스 내 25명의 학생을 무작위로 설문조사했습니다. 성별에 따른 민주당 또는 공화당 학생 수는 아래 표에 나와 있습니다.

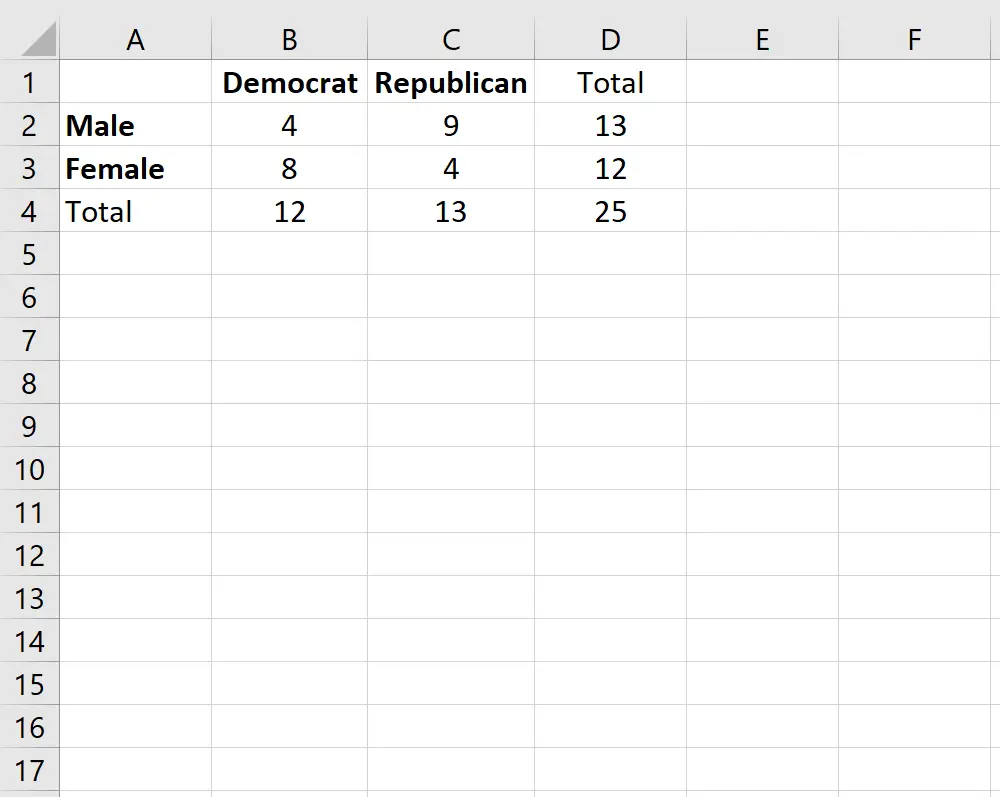
성별과 정당 선호도 사이에 통계적으로 유의미한 연관성이 있는지 확인하기 위해 Fisher의 정확 검정을 수행할 수 있습니다.

Excel에는 이 테스트를 수행하는 기본 제공 함수가 없지만 다음 구문을 사용하는 초기하 함수를 사용하여 테스트를 수행할 수 있습니다.

=HYPGEOM.DIST(sample_s, number_sample, 인구_s, number_pop, 누적)

금:

• Sample_s = 샘플의 “성공” 수
• number_sample = 표본 크기
• Population_s = 모집단의 “성공” 수
• number_pop = 인구 규모
• cumulative = TRUE인 경우 누적 분포 함수를 반환합니다. FALSE인 경우 확률 질량 함수를 반환합니다. 우리의 목적을 위해 우리는 항상 TRUE를 사용합니다.

이 기능을 예제에 적용하기 위해 2×2 테이블의 4개 셀 중 하나를 선택하여 사용할 것입니다. 어떤 셀이든 가능하지만 이 예에서는 값이 “4”인 왼쪽 상단 셀을 사용하겠습니다.

다음으로 함수에 대해 다음 값을 입력합니다.

= HYPGEOM.DIST(개별 셀의 값, 총 열 수, 총 행 수, 총 표본 크기, TRUE)

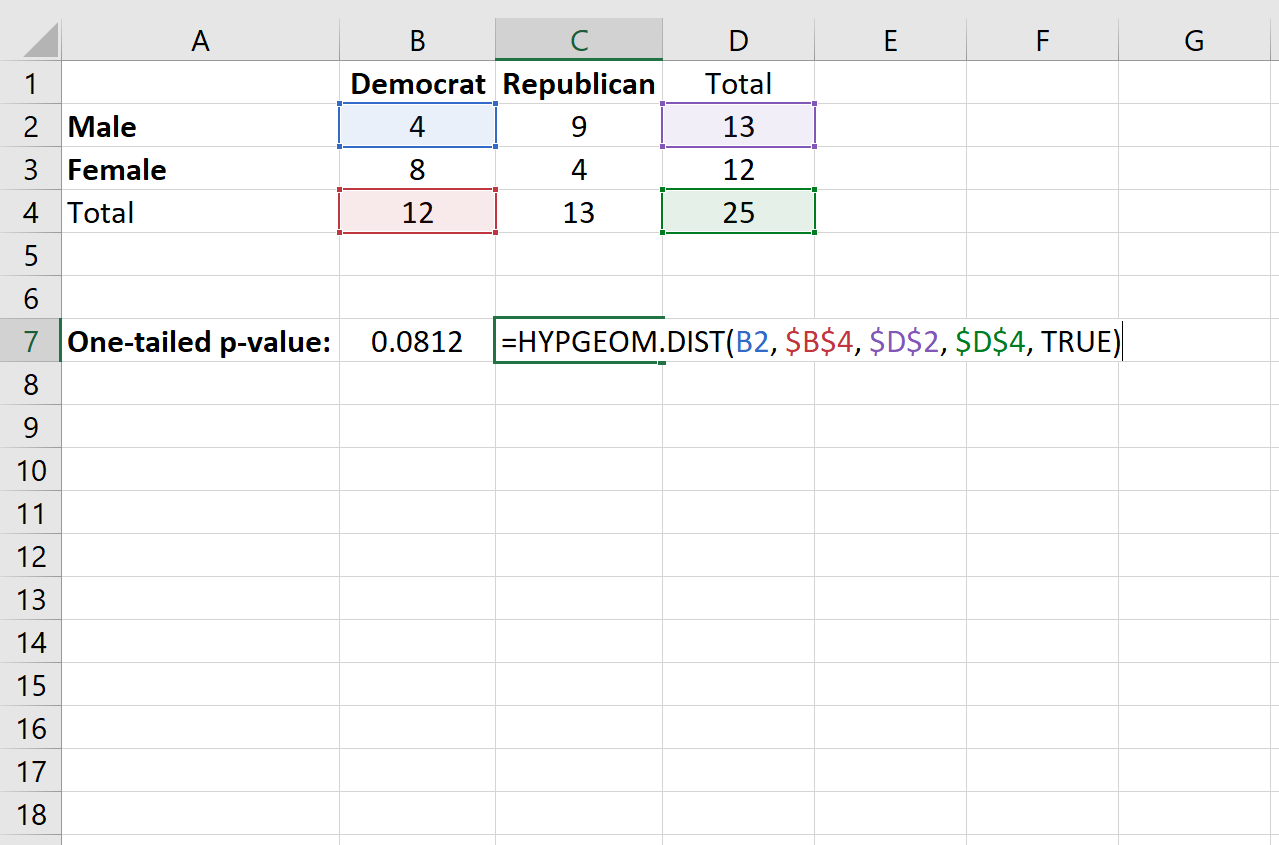
이는 0.0812 의 단측 p-값을 생성합니다.

테스트에 대한 양측 p-값을 찾기 위해 다음 두 가지 확률을 추가합니다.

• 관심 있는 셀에서 x “성공”을 얻을 확률입니다. 우리의 경우 이는 4번 성공할 확률입니다(우리는 이미 이 확률이 0.0812임을 확인했습니다).
• 1 – 관심 있는 셀에서 (총 열 수 – x “성공”)을 얻을 확률입니다. 이 경우 민주당의 총 열 수는 12이므로 1을 찾습니다. – (8개의 “성공” 확률)

우리가 사용할 공식은 다음과 같습니다.

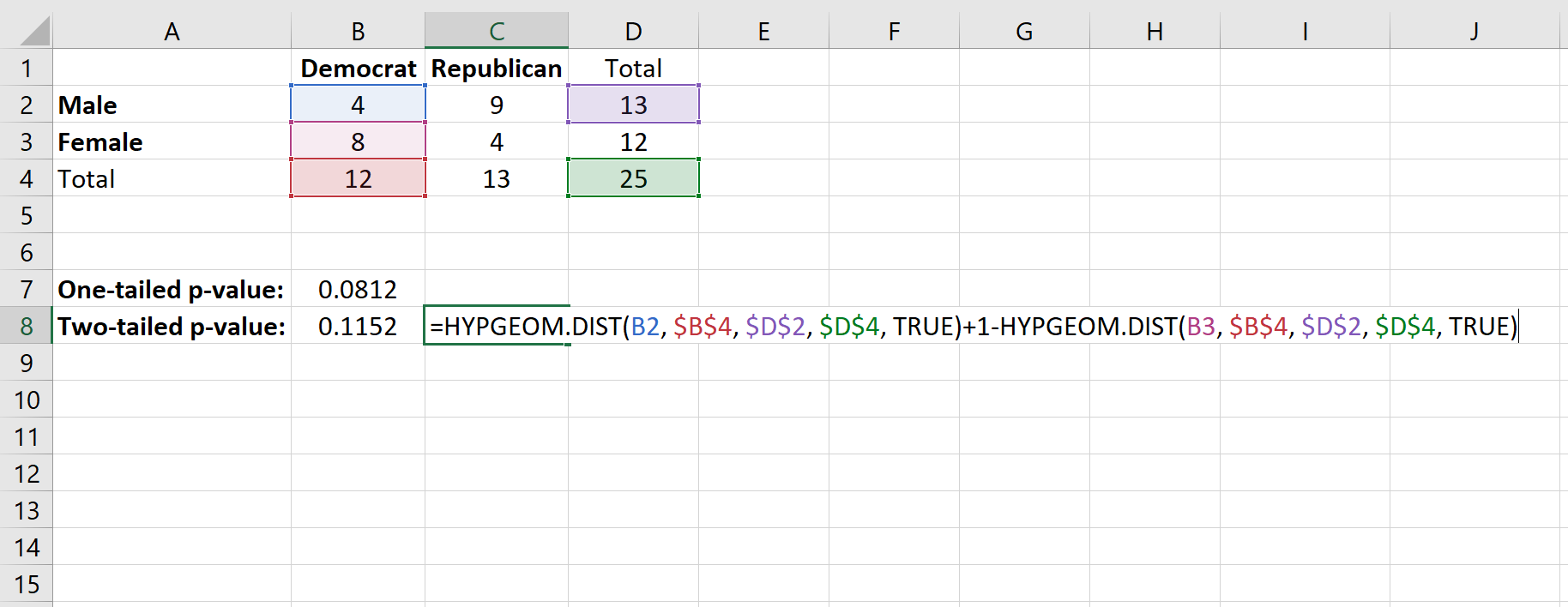
이는 0.1152 의 양측 p-값을 생성합니다.

두 경우 모두 단측 검정을 수행하든 양측 검정을 수행하든 p-값이 0.05 이상이므로 귀무가설을 기각할 수 없습니다. 즉, 성별과 정당 선호도 사이에 유의미한 연관성이 있다고 말할 수 있는 충분한 증거가 없습니다.

추가 리소스

Excel에서 카이제곱 독립성 검정을 수행하는 방법
Excel에서 카이 제곱 적합 테스트를 수행하는 방법
Excel에서 Cramer의 V를 계산하는 방법