Sas에서 2비율 z 테스트를 수행하는 방법
2-비율 z-검정은 두 모집단 비율 간에 통계적으로 유의미한 차이가 있는지 확인하는 데 사용됩니다.
이 테스트에서는 다음과 같은 귀무 가설을 사용합니다.
- H 0 : μ 1 = μ 2 (두 모집단 비율은 동일함)
대립 가설은 양측, 왼쪽 또는 오른쪽일 수 있습니다.
- H 1 (양측): π 1 ≠ π 2 (두 모집단 비율이 동일하지 않음)
- H 1 (왼쪽): π 1 < π 2 (인구 1의 비율이 모집단 2의 비율보다 작음)
- H 1 (오른쪽): π 1 > π 2 (인구 1의 비율이 인구 2의 비율보다 큽니다)
다음 공식을 사용하여 z 테스트 통계량을 계산합니다.
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
여기서 p 1 과 p 2 는 표본 비율이고, n 1 과 n 2 는 표본 크기이며, p는 다음과 같이 계산된 총 합동 비율입니다.
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
z 검정 통계량에 해당하는 p-값이 선택한 유의 수준(일반적으로 선택되는 값은 0.10, 0.05, 0.01)보다 작은 경우 귀무 가설을 기각할 수 있습니다.
다음 예에서는 SAS에서 2비율 z-검정을 수행하는 방법을 보여줍니다.
예: SAS의 2비율 Z 검정
A 카운티의 특정 법률을 지지하는 주민의 비율과 B 카운티의 해당 법률을 지지하는 주민의 비율 사이에 차이가 있는지 알고 싶다고 가정해 보겠습니다.
이를 테스트하기 위해 우리는 각 카운티에서 50명의 주민을 무작위로 추출하여 얼마나 많은 사람들이 법을 지지하는지 계산합니다.
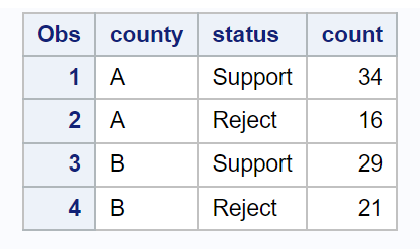
다음 코드는 각 카운티에서 법을 지지하는 주민 수를 요약하는 데이터세트를 만드는 방법을 보여줍니다.
/*create dataset*/ data my_data; input county $status $count; datalines ; A Bracket 34 A Reject 16 B Bracket 29 B Reject 21 ; run ; /*view dataset*/ proc print data =my_data;
그런 다음 Riskdiff(equal var = null) 옵션과 함께 PROC FREQ 문을 사용하여 2-비율 z 테스트를 수행할 수 있습니다.
/*perform two proportion z-test*/
proc freq data =my_data;
weightcount ;
county tables * status / riskdiff ( equal var = null);
run ;
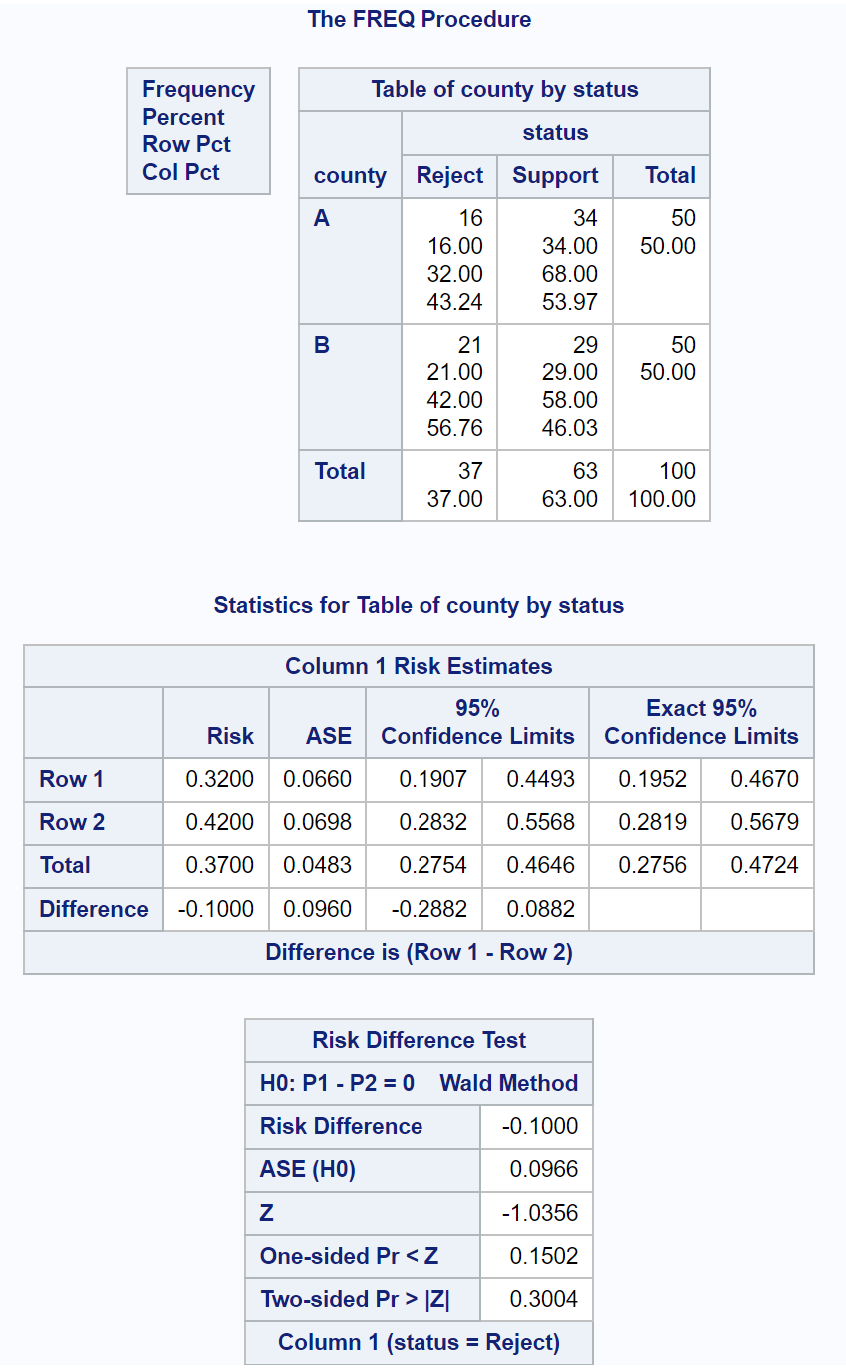
결과 테이블의 위험 차이 테스트 에서 다음 정보를 확인할 수 있습니다.
- Z-테스트 통계: -1.0356
- 양측 p-값: 0.3004
이 특정 2-비율 z-검정에서는 다음 가정을 사용했습니다.
- H 0 : π 1 = π 2 (두 모집단 비율은 동일함)
- H 1 : π 1 ≠ π 2 (두 모집단 비율이 동일하지 않음)
출력의 p-값이 0.05 이상이므로 귀무 가설을 기각할 수 없습니다.
이는 두 카운티 간에 이 법을 지지하는 주민들의 비율이 다르다고 말할 수 있는 충분한 증거가 없다는 것을 의미합니다.
추가 리소스
다음 튜토리얼에서는 SAS에서 기타 일반적인 통계 테스트를 수행하는 방법을 설명합니다.
SAS에서 단일 표본 t-검정을 수행하는 방법
SAS에서 2-표본 t-검정을 수행하는 방법
SAS에서 쌍체 표본 t-검정을 수행하는 방법