Excel에서 vif를 계산하는 방법

회귀분석에서 다중공선성은 두 개 이상의 설명변수가 서로 높은 상관관계를 갖고 있어서 회귀모델에서 고유하거나 독립적인 정보를 제공하지 않는 경우에 발생합니다. 변수 간의 상관 정도가 충분히 높으면 회귀 모델을 피팅하고 해석할 때 문제가 발생할 수 있습니다.

다행스럽게도 회귀 모델에서 설명 변수 간의 상관 관계 및 상관 강도를 측정하는 분산 팽창 계수(VIF) 라는 측정항목을 사용하여 다중 공선성을 탐지할 수 있습니다.

이 튜토리얼에서는 Excel에서 VIF를 계산하는 방법을 설명합니다.

예: Excel에서 VIF 계산

이 예에서는 농구 선수 10명의 속성을 설명하는 다음 데이터 세트를 사용하여 다중 선형 회귀를 수행합니다. 우리는 평가를 반응 변수로 사용하고 포인트, 어시스트, 리바운드를 설명 변수로 사용하여 회귀 모델을 적합화할 것입니다. 다음으로 각 설명변수에 대한 VIF 값을 알아보겠습니다.

1단계: 다중 선형 회귀를 수행합니다.

상단 리본에서 데이터 탭으로 이동하여 데이터 분석을 클릭합니다. 이 옵션이 표시되지 않으면 먼저 무료 Analysis ToolPak 소프트웨어를 설치 해야 합니다 .

데이터 분석을 클릭하면 새 창이 나타납니다. 회귀를 선택하고 확인을 클릭합니다.

반응 변수와 설명 변수에 필요한 표를 완성한 다음 확인을 클릭합니다.

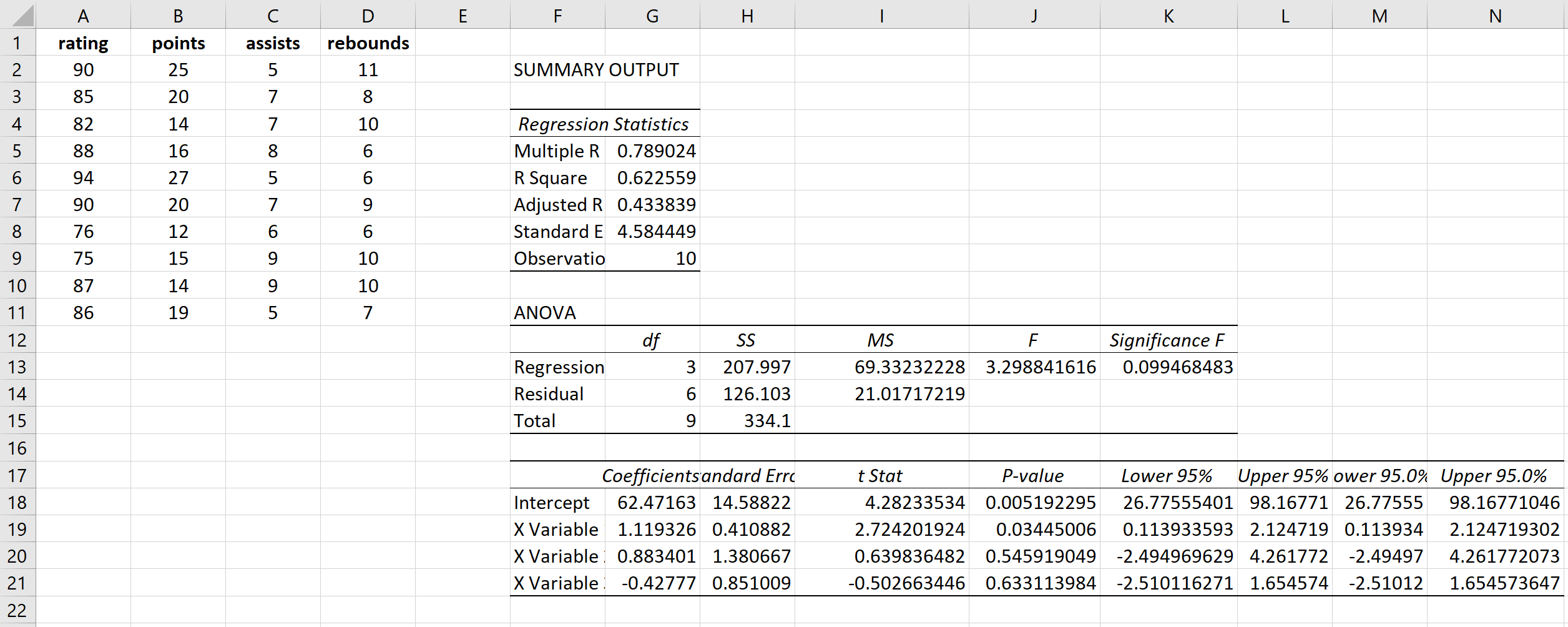
그러면 다음과 같은 결과가 생성됩니다.

2단계: 각 설명 변수에 대한 VIF를 계산합니다.

다음으로 설명 변수 하나를 반응 변수로, 나머지 두 개를 설명 변수로 사용하여 개별 회귀를 수행하여 세 가지 설명 변수 각각에 대한 VIF를 계산할 수 있습니다.

예를 들어, 포인트 를 응답 변수로 사용하고 어시스트 와 리바운드 를 설명 변수로 사용하여 다중 선형 회귀를 수행하여 포인트 변수에 대한 VIF를 계산할 수 있습니다.

그러면 다음과 같은 결과가 생성됩니다.

포인트 의 VIF는 1 / (1 – R 제곱) = 1 / (1 – .433099) = 1.76 으로 계산됩니다.

그런 다음 다른 두 변수인 어시스트 와 리바운드 에 대해 이 프로세스를 반복할 수 있습니다.

세 가지 설명 변수에 대한 VIF는 다음과 같습니다.

포인트: 1.76
어시스트: 1.96
리바운드: 1.18

VIF 값을 해석하는 방법

VIF 값은 1부터 시작하며 상한이 없습니다. VIF를 해석하는 일반적인 규칙은 다음과 같습니다.

• 값 1은 주어진 설명 변수와 모델의 다른 설명 변수 사이에 상관 관계가 없음을 나타냅니다.
• 1과 5 사이의 값은 주어진 설명 변수와 모델의 다른 설명 변수 사이의 중간 정도의 상관 관계를 나타내지만 특별한 주의가 필요할 만큼 심각하지는 않은 경우가 많습니다.
• 5보다 큰 값은 주어진 설명 변수와 모델의 다른 설명 변수 사이에 잠재적으로 심각한 상관 관계가 있음을 나타냅니다. 이 경우 회귀 결과의 계수 추정치와 p-값은 신뢰할 수 없을 가능성이 높습니다.

우리 회귀 모델의 설명 변수의 각 VIF 값은 1에 가깝기 때문에 우리 예에서는 다중 공선성이 문제가 되지 않습니다.