와이블 분포
이 기사에서는 Weibull 분포가 무엇인지, 그리고 어떤 용도로 사용되는지 설명합니다. 또한 Weibull 분포의 그래픽 표현과 이러한 유형의 확률 분포의 속성을 볼 수 있습니다.
Weibull 분포란 무엇입니까?
Weibull 분포는 형상 매개변수 α와 척도 매개변수 λ라는 두 가지 특성 매개변수로 정의되는 연속 확률 분포입니다.
통계에서는 생존분석을 위해 주로 Weibull 분포를 사용합니다. 마찬가지로 Weibull 분포는 다양한 분야에 많이 적용됩니다. 아래에서는 Weibull 분포를 사용하는 방법에 대해 자세히 설명하겠습니다.
![]()
저자에 따르면 Weibull 분포는 세 가지 매개변수를 사용하여 매개변수화할 수도 있습니다. 그런 다음 분포 그래프가 시작되는 가로좌표를 나타내는 임계값이라는 세 번째 매개변수가 추가됩니다.
Weibull 분포는 1951년에 이를 자세히 설명한 스웨덴 Waloddi Weibull의 이름을 따서 명명되었습니다. 그러나 Weibull 분포는 1927년 Maurice Fréchet에 의해 발견되었고 1933년 Rosin과 Rammler에 의해 처음 적용되었습니다.
Weibull 분포 도표화
Weibull 분포의 정의를 확인한 후에는 해당 매개변수 값에 따라 그래픽 표현이 어떻게 달라지는지 살펴보겠습니다.
아래에서는 Weibull 분포의 밀도 함수 그래프가 형상 매개변수와 척도 매개변수의 값에 따라 어떻게 달라지는지 보여주는 몇 가지 예를 볼 수 있습니다.
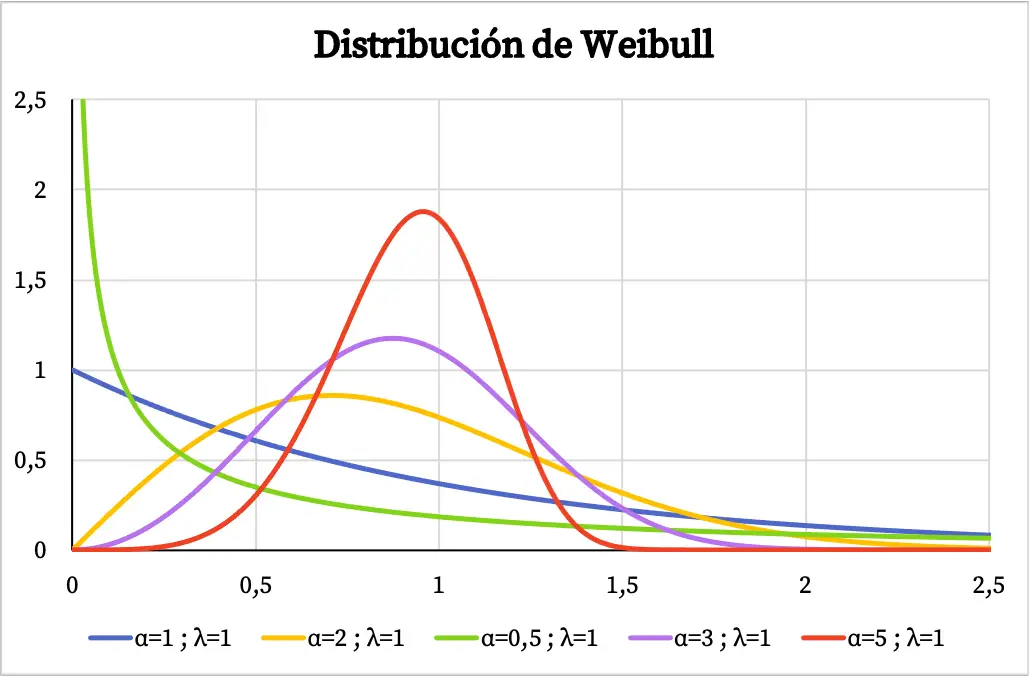
Weibull 분포를 사용하여 시스템의 고장률을 시간 함수로 모델링하는 경우 형상 모수 α의 값은 다음을 의미합니다.
- α<1: 시간이 지남에 따라 고장률이 감소합니다.
- α=1: 실패율은 시간이 지나도 일정합니다.
- α>1: 시간이 지남에 따라 실패율이 증가합니다.
한편, 다음 그래프에서는 Weibull 분포의 특성값을 기준으로 플롯된 누적확률함수를 확인할 수 있습니다.
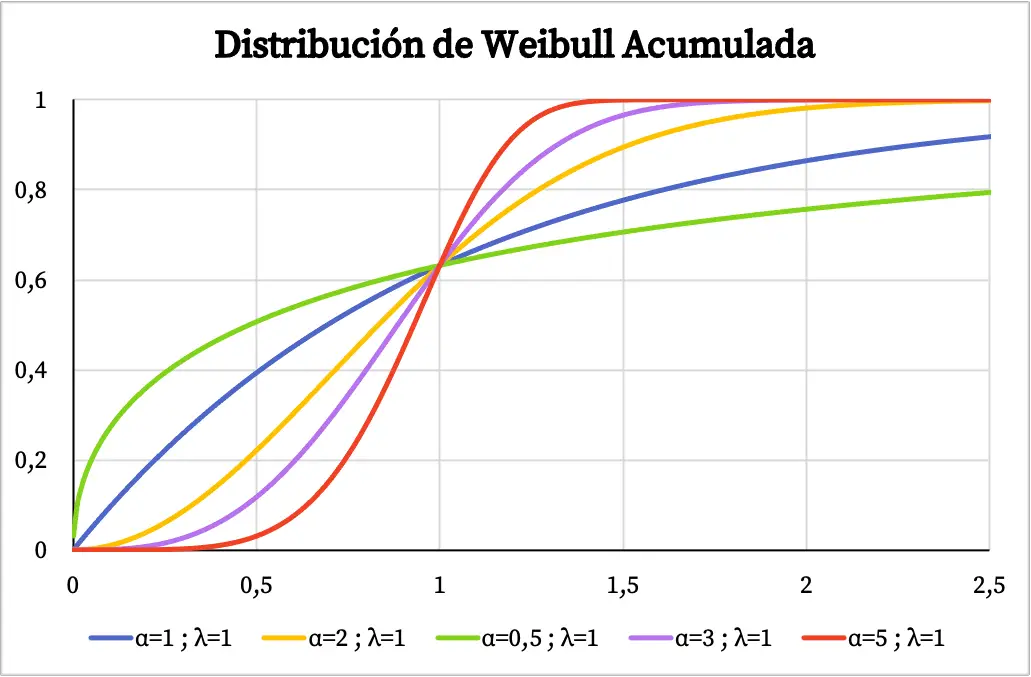
Weibull 분포의 특성
Weibull 분포는 다음과 같은 특징을 가지고 있습니다.
- Weibull 분포에는 그래프를 정의하는 두 가지 특성 매개변수인 형상 매개변수 α와 척도 매개변수 λ가 있습니다. 두 매개변수 모두 양의 실수입니다.
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Weibull 분포는 양의 가로좌표 값만 허용합니다.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- Weibull 분포의 평균은 다음 공식으로 계산됩니다.
![]()
- 한편, Weibull 분포의 분산을 찾는 공식은 다음과 같습니다.
![]()
- α>1인 Weibull 분포를 따르는 확률 변수의 모드는 다음 식으로 결정할 수 있습니다.
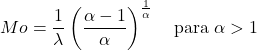
![]()
- 마찬가지로 Weibull 분포의 누적 확률 함수 공식은 다음과 같습니다.
![]()
- Weibull 분포의 비대칭 계수는 다음 공식을 적용하여 계산됩니다.
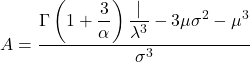
- 마지막으로 Weibull 분포의 첨도 계수를 결정할 수 있는 공식은 다음과 같습니다.
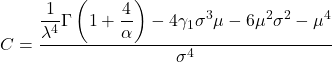
금
![]()
Weibull 분포의 응용
Weibull 분포에는 다음을 포함하여 다양한 응용 프로그램이 있습니다.
- 응용통계에서는 생존분석에 Weibull 분포를 사용한다.
- 공학에서는 Weibull 분포를 사용하여 제조 시간과 관련된 기능을 모델링합니다.
- 레이더 시스템에서 수신된 신호의 분산을 시뮬레이션합니다.
- 보험 부문에서는 청구 범위를 모델링합니다.
- 예를 들어 기상학에서는 다양한 풍속의 빈도를 모델링합니다.