Wilcoxon 부호 순위 테스트를 수행하는 방법

Wilcoxon 부호 순위 테스트는 대응 t 테스트 의 비모수적 버전입니다. 두 모집단 평균 사이에 유의미한 차이가 있는지 여부를 테스트하는 데 사용됩니다.

Wilcoxon 부호 순위 테스트를 사용해야 하는 경우

쌍 t 검정을 사용하고 싶지만 쌍 간의 차이 분포가 심각 하게 비정규 분포를 따르는 경우 Wilcoxon Signed Rank 검정을 사용하십시오.

차이가 정규 분포를 따르지 않는지 확인하는 가장 쉬운 방법은 차이에 대한 히스토그램을 만들고 어느 정도 정규적인 “종” 모양 분포를 따르는지 확인하는 것입니다.

쌍체 t 검정은 정규성 편차에 대해 매우 견고하므로 정규 분포와의 편차는 Wilcoxon 부호 순위 검정의 사용을 정당화할 만큼 충분히 커야 합니다.

Wilcoxon Signed Rank Test 응시 방법

다음 예에서는 Wilcoxon 부호 순위 테스트를 수행하는 방법을 보여줍니다.

한 농구 코치가 특정 훈련 프로그램이 선수의 자유투 횟수를 증가시키는지 알고 싶어합니다. 이를 테스트하기 위해 그는 15명의 선수에게 훈련 프로그램 전후에 각각 20개의 자유투를 시도하도록 요청했습니다.

각 선수는 자신과 “페어링”될 수 있으므로 코치는 훈련 프로그램 전후의 평균 자유투 횟수에 유의미한 차이가 있는지 확인하기 위해 페어링된 t-테스트를 사용할 계획이었습니다. 훈련.

그러나 차이의 분포는 비정규적인 것으로 밝혀졌으므로 코치는 대신 Wilcoxon 부호 순위 테스트를 사용합니다.

다음 표는 훈련 프로그램 전후에 15명의 선수 각각이 시도한 자유투 횟수(20회 시도 중)를 나타냅니다.

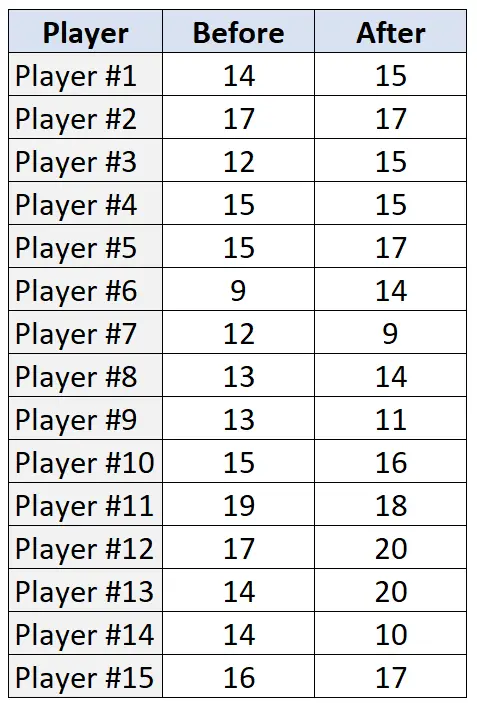
1단계: 귀무가설과 대립가설을 진술합니다.

H ₀ : 두 그룹 간의 차이 중앙값이 0입니다.

H _A : 차이의 중앙값은 음수입니다. (예: 선수들은 훈련 프로그램에 참여하기 전에 더 적은 수의 자유투를 가합니다.)

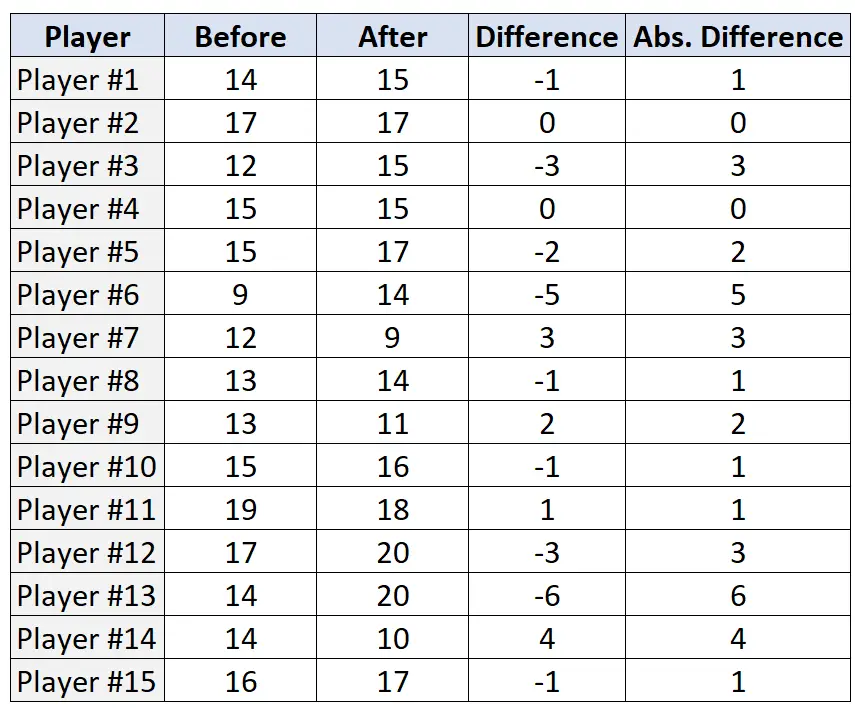
2단계: 각 쌍의 차이와 절대차를 구합니다.

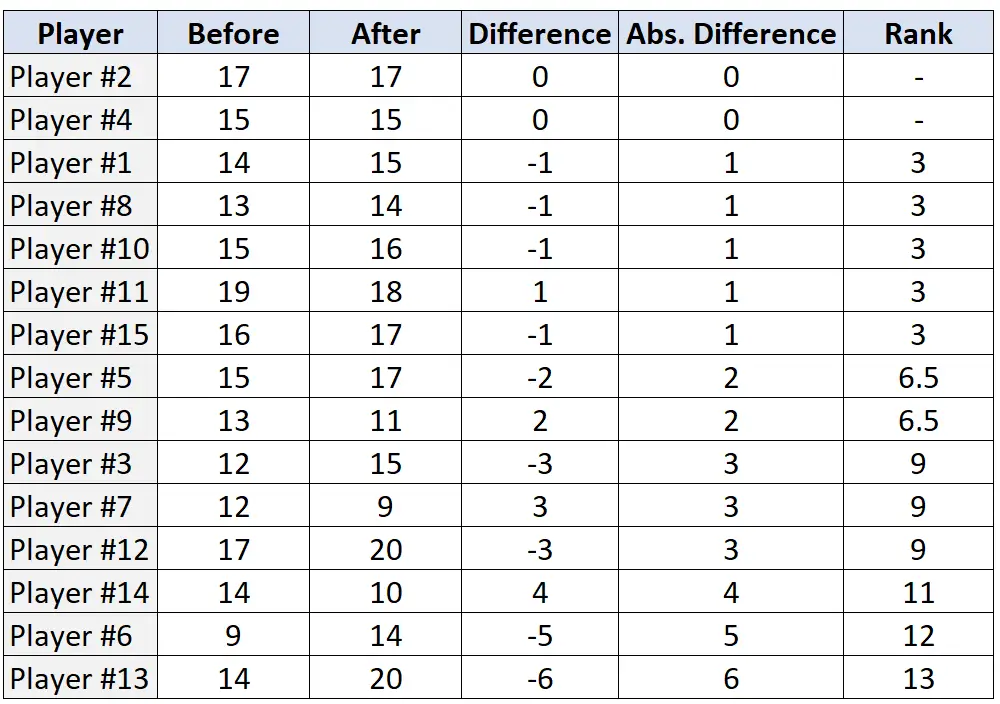
3단계: 절대 차이를 기준으로 쌍의 순위를 지정하고 절대 차이가 가장 작은 것부터 가장 큰 것까지 순위를 지정합니다. 절대차가 “0”인 쌍은 무시하고 동점인 경우 평균 순위를 지정합니다.

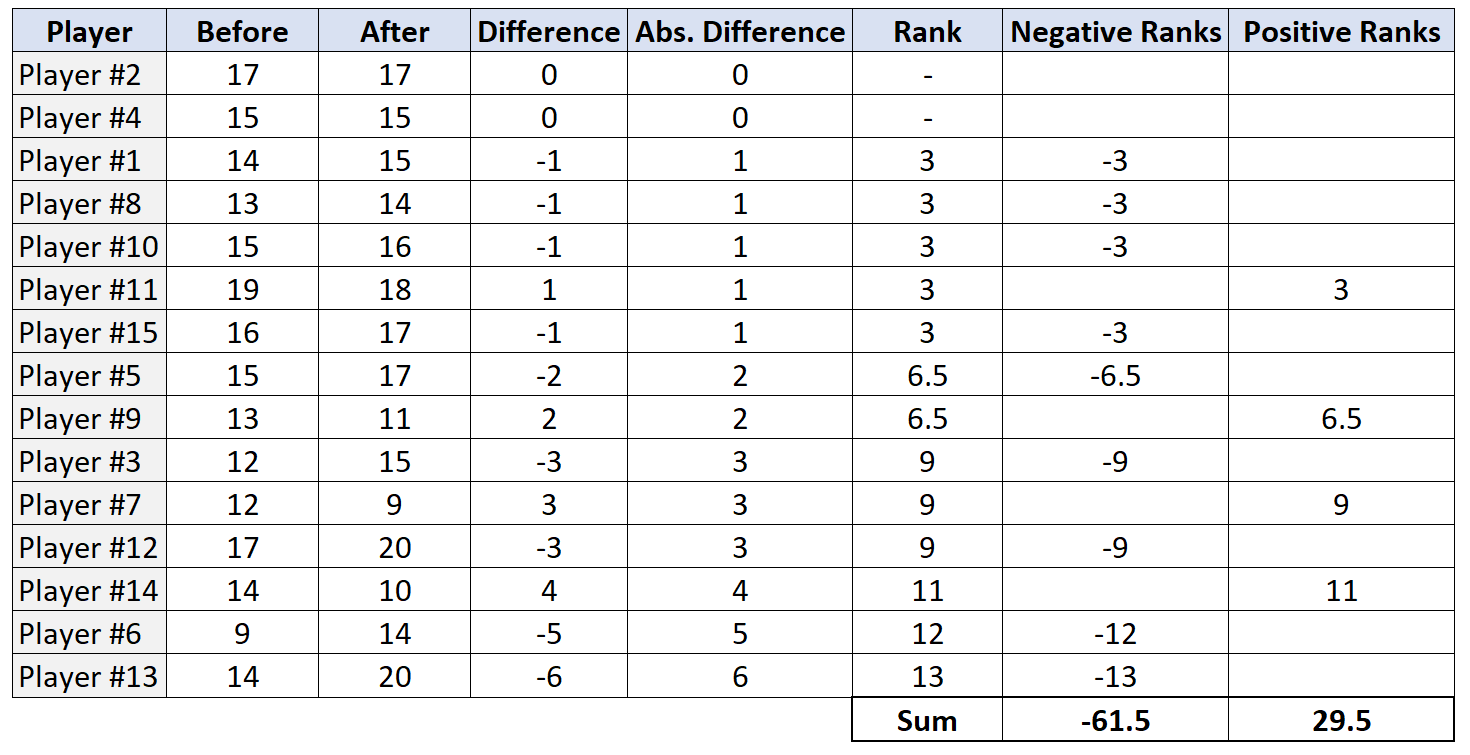
4단계: 양수 순위와 음수 순위의 합을 구합니다.

5단계: 귀무가설을 기각하거나 기각하지 않습니다.

검정 통계량 W는 양수 순위와 음수 순위의 절대값 중 가장 작은 값입니다. 이 경우 가장 작은 값은 29.5입니다. 따라서 테스트 통계는 W = 29.5 입니다.

귀무 가설을 기각해야 하는지 여부를 결정하기 위해 n 및 선택한 알파 수준에 해당하는 Wilcoxon 부호 순위 테스트 임계값 테이블 에서 찾은 임계값을 참조할 수 있습니다.

검정 통계량 W가 표의 임계값 보다 작거나 같으면 귀무 가설을 기각할 수 있습니다. 그렇지 않으면 귀무가설을 기각하지 못할 것입니다.

알파 수준 0.05 및 n = 13(총 쌍 수에서 관찰된 차이가 0이기 때문에 순위를 계산하지 않은 두 쌍을 뺀 값)에 해당하는 임계값은 17 입니다.

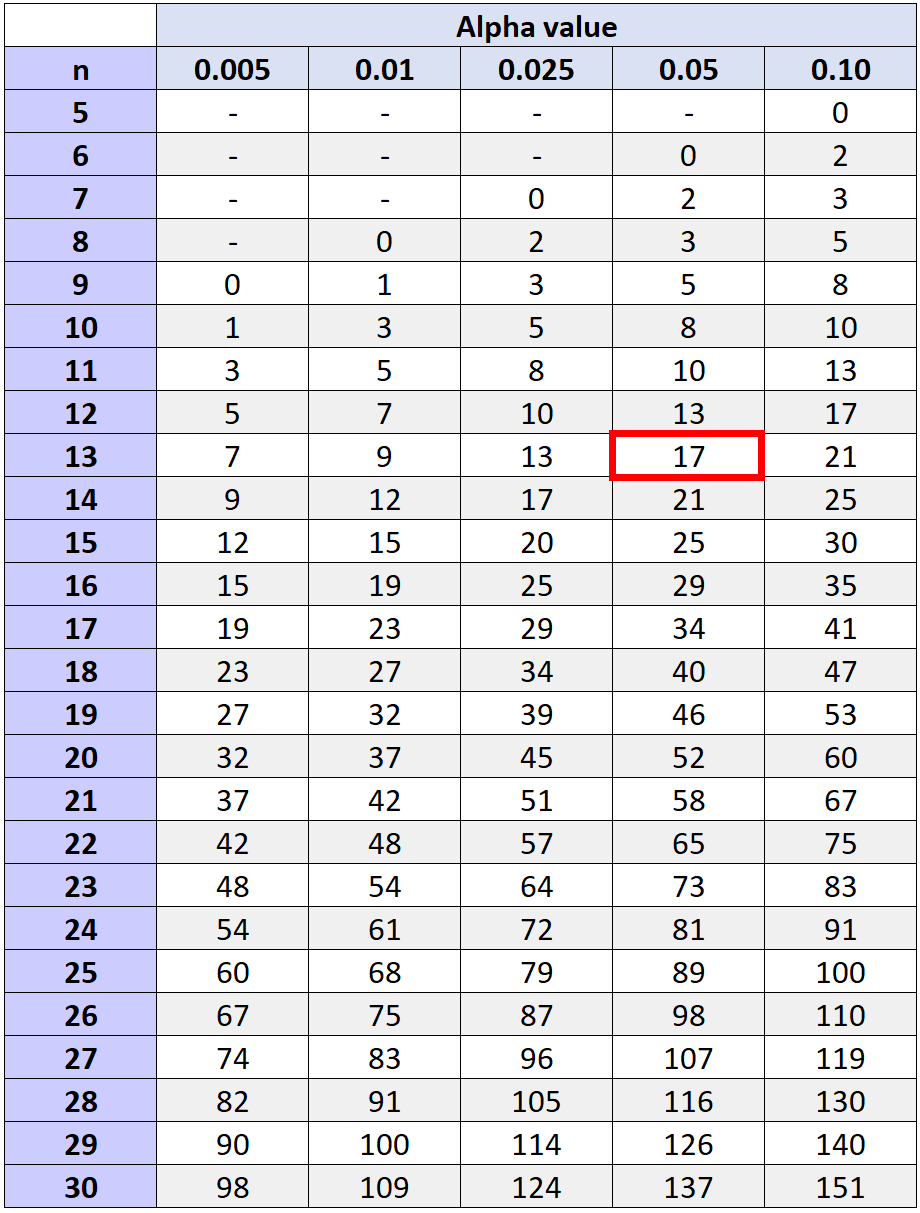
검정 통계량(W = 29.5)이 17보다 작거나 같지 않으므로 귀무 가설을 기각할 수 없습니다. 훈련 프로그램이 선수들의 자유투 횟수를 크게 증가시킨다고 말할 수 있는 충분한 증거가 없습니다.

참고: 손으로 테스트하는 대신 계산기를 사용하여 테스트를 수행하려면 Wilcoxon 부호 순위 테스트 계산기를 사용하세요.