조건부 확률(또는 조건부 확률)

여기에서는 조건부 확률(또는 조건부 확률)이 무엇인지 알아봅니다. 조건부 확률이 어떻게 계산되는지 예제와 이러한 유형의 확률의 속성을 설명합니다. 또한, 단계별로 풀이된 조건부 확률 연습문제도 함께 연습할 수 있습니다.

조건부 확률이란 무엇입니까?

조건부 확률 이라고도 하는 조건부 확률은 다른 사건 B가 발생하면 사건 A가 발생할 확률을 나타내는 통계적 척도입니다. 즉, 조건부 확률 P(A|B)는 사건 B가 이미 발생한 후에 사건 A가 발생할 확률을 의미합니다.

조건부 확률은 두 사건 사이에 수직 막대(P(A|B))로 작성되며 “사건 B가 주어진 경우 사건 A의 조건부 확률”이라고 읽습니다.

조건부 확률 값은 0과 1 사이의 숫자입니다. 조건부 확률이 높을수록 사건 B가 발생할 때 사건 A가 발생할 가능성이 높아지고, 조건부 확률이 낮을수록 사건 A가 발생할 가능성이 낮아집니다. 이벤트 B가 발생하면 발생합니다.

조건부 확률 공식

사건 B가 주어졌을 때 사건 A의 조건부 확률은 사건 A와 사건 B의 교차 확률을 사건 B의 확률로 나눈 값과 같습니다.

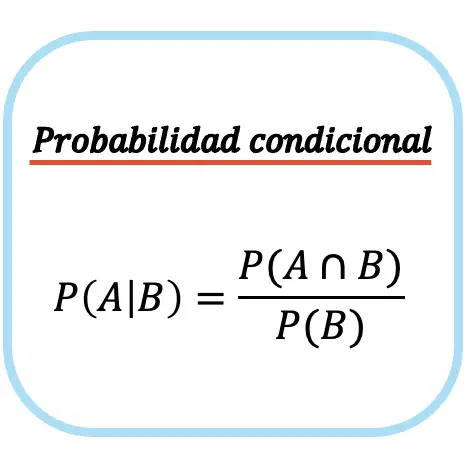
조건부 확률(또는 조건부 확률) 공식은 무조건 사건의 발생 확률이 0이 아닌 경우, 즉 P(B)≠0인 경우에만 사용할 수 있습니다. 즉, 사건 B가 발생할 수 있는 경우입니다.

조건부 확률은 역으로 계산할 수도 있습니다. 즉, P(B|A)를 알고 있으면 P(A|B)를 결정할 수 있습니다. 하지만 이렇게 하려면 베이즈 정리를 적용해야 합니다. 이 정리가 여기에서 무엇으로 구성되어 있는지 확인할 수 있습니다.

조건부 확률의 예

조건부 확률의 정의와 공식이 무엇인지 살펴본 후에는 이러한 유형의 확률의 예를 단계별로 풀어 그 의미를 완전히 이해할 것입니다.

• 30명의 학생을 대상으로 시험을 치른 후, 몇 명의 학생이 공부하고 몇 명이 합격했는지 알아보기 위해 데이터를 수집했습니다. 결과는 다음 분할표에 나와 있습니다. 수집된 데이터에서 이미 공부한 경우 시험에 합격할 조건부 확률을 계산합니다.

조건부 확률을 얻으려면 이전에 본 공식을 적용해야 합니다.

그러므로 먼저 학생이 공부하고 공부해서 합격할 확률을 구해야 합니다. 학생이 공부할 확률을 찾으려면 라플라스의 법칙을 사용하면 됩니다. 즉, 공부한 학생 수를 총 관찰 수로 나누면 됩니다.

그리고 공부하고 합격한 학생 수를 전체로 나누어 분할표에서 한 학생이 동시에 공부하고 합격할 확률을 알아낼 수 있습니다.

따라서 학생이 공부한 경우 시험에 합격할 확률은 다음과 같습니다.

종속 사건과 독립 사건의 조건부 확률

이 섹션에서는 조건부 확률과 종속 및 독립 이벤트(또는 종속 및 독립 이벤트) 사이의 관계가 무엇인지 살펴보겠습니다. 왜냐하면 서로 다른 개념임에도 불구하고 이 두 가지 유형의 사건은 조건부 확률과 연결되어 있기 때문입니다.

두 사건(또는 발생)은 발생 확률이 서로 의존하지 않는 경우 독립적입니다. 이러한 경우 두 사건 간의 교차점은 각 사건의 확률을 개별적으로 곱한 것과 동일합니다. 따라서 조건부 확률 공식은 다음과 같이 단순화됩니다.

즉, 사건 A와 B가 독립이면 사건 B가 주어졌을 때 사건 A의 조건부 확률은 사건 A가 발생할 확률과 정확히 같습니다.

반면, 두 사건이 종속적이라는 것은 한 사건의 확률이 다른 사건의 확률에 의존한다는 것을 의미합니다. 따라서 두 사건 A와 B가 종속적일 때 사건 B가 주어졌을 때 사건 A의 조건부 확률은 사건 A의 발생 확률과 다릅니다.

해결 조건부 확률 연습

연습 1

우리는 공이 가득한 가방에 절반은 주황색이고 나머지 절반은 녹색이라는 것을 알고 있습니다. 또한 모든 공의 1/3은 주황색이며 동시에 표지판이 표시되어 있습니다. 주황색 공을 뽑았을 때 신호를 받을 확률은 얼마입니까?

문제를 해결하려면 다음과 같은 조건부 공식 확률을 적용해야 합니다.

문제 설명은 가방의 절반이 오렌지라는 것을 알려줍니다. 따라서 주황색 공을 집을 확률은 이론적으로 50%입니다.

반면에 우리는 전체의 1/3이 주황색 공이고 신호가 있다는 것을 알고 있으므로 신호가 있는 주황색 공을 얻을 확률은 다음과 같습니다.

마지막으로 계산된 확률을 조건부 확률 공식에 대체하여 해당 값을 찾습니다.

요약하면, 주황색일 경우 신호에 따라 공을 뽑을 확률은 66%입니다.

연습 2

상자에 파란색 펜 6개와 검은색 펜 3개가 있다면 파란색 펜 1개를 뽑을 확률과 파란색 펜 2개를 연속으로 뽑을 확률을 계산해 보세요.

파란색 펜을 한 번 집을 수 있는 확률을 확인하려면 간단히 라플라스의 법칙을 사용하세요.

문제는 또한 두 개의 파란색 펜을 연속적으로 집을 확률, 즉 이전에 이미 파란색 펜을 집은 경우 파란색 펜을 집는 조건부 확률을 알려달라고 요청합니다.

파란색 펜을 그리면 불리한 경우가 생기지만, 전체에서 펜이 하나 줄어드는 경우도 있습니다. 따라서 조건부 확률은 다음과 같습니다.

연습 3

동전을 던져서 앞면이 나온다면 주사위를 굴려 숫자 4가 나올 조건부 확률은 얼마입니까?

이 연습문제를 해결하려면 조건부 확률 이론을 고려해야 합니다. “주사위를 던져 숫자 4를 얻는 것” 과 “동전을 던져 앞면을 얻는 것” 은 독립적이기 때문입니다. 따라서 조건부 확률 공식을 사용할 필요는 없지만 다음 등식이 충족됩니다.

따라서 조건부 확률을 찾으려면 Laplace의 규칙을 사용하면 됩니다.

연습 4

한 국가의 25개 기업을 대상으로 회계연도를 조사하고, 해당 기업의 주가가 해당 연도의 경제적 결과에 따라 어떻게 변하는지를 조사했습니다. 다음 분할표에서 수집된 데이터를 볼 수 있습니다.

지난 1년 동안 이익을 낸 기업의 주가가 상승할 가능성은 얼마나 됩니까?

이 연습에서는 회사가 긍정적인 경제적 결과를 달성한 경우 주식이 상승할 조건부 확률에 대해 묻습니다. 따라서 이 확률을 계산하려면 조건부 확률 공식을 사용해야 합니다.

따라서 먼저 회사가 이익을 낼 확률을 계산하고, 두 번째로 회사가 주당 가격을 높이면서 경제적 이익을 얻을 확률을 계산합니다.

그런 다음 찾은 값을 공식에 대입하고 조건부 확률을 계산합니다.

조건부 확률의 속성

조건부 확률 또는 조건부 확률의 속성은 다음과 같습니다.

• 사건 B가 주어졌을 때 사건 A의 조건부 확률과 사건 B가 주어졌을 때 상보적인 사건 A의 조건부 확률의 합은 1과 같습니다.

• 사건 A가 사건 B의 하위 집합인 경우 B가 참일 때 A는 항상 발생합니다. 따라서 이 경우 사건 B가 주어졌을 때 사건 A의 조건부 확률은 1입니다.

• 두 가지 다른 사건이 주어지면 조건부 확률과 관련하여 다음과 같은 동일성이 항상 유지됩니다.