체비쇼프의 정리

이 문서에서는 체비쇼프의 정리가 무엇인지 설명합니다. 여기서는 체비쇼프 정리 공식, 해결된 연습 문제 및 온라인 체비쇼프 정리 계산기를 찾을 수 있습니다. 마지막으로 체비쇼프의 정리와 경험적 법칙의 차이를 보여준다.

체비쇼프의 정리는 무엇입니까?

체비쇼프의 불평등(Chebyshev’s inequality) 이라고도 알려진 체비쇼프 정리(Chebyshev ‘s theorem )는 임의 변수의 값이 평균에서 특정 거리 내에 있을 확률을 계산하는 데 사용되는 통계 규칙입니다.

즉, 통계에서는 체비쇼프의 정리를 사용하여 값이 신뢰 구간 내에 있을 확률을 결정합니다.

또한 체비쇼프의 정리는 대수의 법칙과 같은 다른 통계 정리를 증명하는 데에도 사용됩니다.

체비쇼프의 정리는 프랑스인 Irénée-Jules Bienaymé에 의해 처음 공식화되었지만, 이 정리는 1867년 러시아인 Pafnuty Chebushev에 의해 창시되었기 때문에 그렇게 명명되었습니다.

체비쇼프 정리의 공식

체비쇼프의 정리에 따르면 값이 평균에서 k 표준 편차와 같을 확률은 1에서 1을 k 제곱으로 나눈 비율을 뺀 값보다 크거나 같습니다.

따라서 체비쇼프 정리의 공식은 다음과 같습니다.

금

는 랜덤 변수의 값이고,

변수의 산술 평균 ,

표준편차 와

확률을 계산할 평균과의 표준 편차 수입니다.

이 공식은 계산이 수행되는 표준 편차 수가 1보다 큰 경우, 즉 k 가 1보다 큰 경우에만 사용할 수 있습니다.

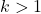아래의 온라인 체비쇼프 정리 계산기를 사용하여 확률을 계산할 수 있습니다.

체비쇼프 정리의 예

체비쇼프 정리의 정의와 그 공식이 무엇인지 살펴본 후, 개념을 더 잘 이해할 수 있도록 이 통계 정리의 해결된 예를 살펴보겠습니다.

• 대학의 교과목 성적을 평균 65, 표준편차 10의 분포로 정의한다면, 50점에서 80점 사이의 성적을 받은 학생의 비율은 몇 퍼센트입니까?

이 문제를 해결하려면 체비쇼프의 정리 공식을 적용해야 합니다. 그러나 먼저 값 50과 80이 변수 평균과 얼마나 많은 표준 편차를 가지고 있는지 결정해야 합니다. 이를 위해서는 다음 계산을 수행하면 됩니다.

따라서 값 50과 80은 각각 하한 평균과 상한 평균으로부터 1.5 표준편차에 해당합니다. 따라서 k=1.5인 체비셰바 정리의 공식을 사용합니다.

따라서 최소 55.56%의 학생이 50~80점 사이의 성적을 받았습니다.

체비쇼프의 정리 계산기

해당 값과 평균 (k) 사이의 표준 편차 수를 입력한 다음 “계산”을 클릭합니다. 그러면 계산기는 신뢰 구간의 최소 확률을 반환합니다.

소수점 구분 기호로 점을 사용하여 표준 편차 수를 입력해야 합니다.

체비쇼프의 정리와 경험 법칙

통계에서 밀접하게 관련된 두 가지 개념은 체비쇼프의 정리와 경험적 규칙입니다. 둘 다 신뢰 구간의 확률을 계산하는 데 사용되기 때문입니다.

체비쇼프의 정리와 경험적 규칙의 차이점은 체비쇼프의 정리는 모든 유형의 분포에 사용할 수 있는 반면, 경험적 규칙은 정규 분포에만 유효하다는 것입니다.

따라서 체비쇼프 정리의 사용은 더 광범위하지만 경험적 규칙은 정규 분포에 대해 더 정확한 결과를 제공합니다.

경험 법칙이 무엇인지 정확히 보려면 여기를 클릭하십시오.